
Методы машинного обучения
Шестаков Андрей (avshestakov@hse.ru)
Выявление сообществ на сети, структурная схожесть
Повторим меры центральности¶
nx.draw_networkx(g, pos=layout, )
Degree centrality¶
Самая оцевидная центральность - просто степень узла. Характеризует некоторую популярность узла (много друзей, много связей).
$$ C_d(i) = k(i) = \sum_jA_{ij} = \sum_iA_{ij}$$$$ \bar{C}_d(i) = \frac{1}{n-1} C_d(i)$$Существует обобщение на ориентированные (prestige) и взвешенные сети.
nx.draw_networkx(g, pos=layout, node_size=degr)
degr_cent
{0: 0.4, 1: 0.4, 2: 0.4, 3: 0.6000000000000001, 4: 0.4, 5: 0.2}
Closeness centrality¶
Центральность, основанная на расстоянии до остальных вершин в графе.
$$ C_{cl}(i) = \frac{1}{\sum_j d(i,j)} $$$$ \bar{C}_{cl}(i) = (n-1) \cdot C_{cl}(i) $$Актор, расположенный в центре сети может быстро добраться до остальных акторов. Акторы на периферии расположены дальше.
Вопрос: что будет, если граф окажется несвязным?
nx.draw_networkx(g, pos=layout, node_size=closeness_nodes_values)
closeness_nodes
{0: 0.45454545454545453,
1: 0.5555555555555556,
2: 0.5555555555555556,
3: 0.7142857142857143,
4: 0.5555555555555556,
5: 0.38461538461538464}
Betweenness centrality (nodes)¶
Пусть $\sigma_{st}$ - количество кратчайших путей между вершинами $s$ и $t$, а $\sigma_{st}(i)$ - кр. пути между $v_s$ и $v_t$, которые проходят через вершину $v_i$.
Тогда $$ C_b(i) = \sum\limits_{s\neq t\neq i} \frac{\sigma_{st}(i)}{\sigma_{st}} $$
$$ \bar{C}_b(i) = \frac{2}{(n-1)(n-2)}C_b(i) $$nx.draw_networkx(g, pos=layout, node_size=betw_nodes_values)
betw_nodes
{0: 0.05,
1: 0.15000000000000002,
2: 0.15000000000000002,
3: 0.65,
4: 0.4,
5: 0.0}
Betweenness centrality (edges)¶
Betweenness также можно расчитывать для ребер! Давайте определим для каких ребер она наибольшая и что это может нам дать?
nx.draw_networkx(g, pos=layout)
df.sort_values('betw', ascending=False, )
| source | target | betw | |
|---|---|---|---|
| 4 | 3 | 4 | 0.533333 |
| 2 | 1 | 3 | 0.333333 |
| 3 | 2 | 3 | 0.333333 |
| 5 | 4 | 5 | 0.333333 |
| 0 | 0 | 1 | 0.200000 |
| 1 | 0 | 2 | 0.200000 |
Page Rank¶
Идея PageRank заключается в попытке описать блуждание по вершинам графа. Вероятность перехода в вершину $v_i$ обратнопропорциональна степеням входящих связанных с ней вершин.
$$p^{t+1} = (D^{-1}A)^\top p^t = P^\top p^t$$Помимо случайного блуждания между соседними вершинами заложен механизм "телепорта" между случайными вершинами с вероятностью $1-\alpha$.
$$ \mathbb{P} = \alpha P + \frac{(1 - \alpha)}{n} E,$$где $E$ - это матрица состоящая из единиц.
Вектор Page Rank является одним из решений задачи на поиск собственного числа матрицы $\mathbb{P}$
$$\mathbb{P}^\top p = \lambda p$$nx.draw_networkx(g, pos=layout, node_size=pr)
pr_nodes
{0: 0.16195310432472196,
1: 0.16112205885619568,
2: 0.16112205885619568,
3: 0.2375,
4: 0.17775588228760858,
5: 0.10054689567527803}
"Геометрическая" центральность¶
Eccentricity - максимальная длина кратчайшего пути из вершины $i$ до всех остальных вершин $e(i) = \max\limits_j d(i, j)$.
Диаметр - $\max e(i)$
Радиус - $\min e(i)$
Центральными вершинами являются те, у которых $e(i)$ равна радиусу графа
print(nx.radius(g))
print(nx.diameter(g))
2 4
nx.draw_networkx(g, pos=layout)
nx.draw_networkx(g, pos=layout, node_size=ecc)
ecc_nodes
{0: 4, 1: 3, 2: 3, 3: 2, 4: 3, 5: 4}
Clustering coefficient¶
Доля "треугольников" в среди соседей вершины.
nx.draw_networkx(g, pos=layout)
g.add_edge(1,2)
nx.draw_networkx(g, pos=layout)
nx.triangles(g)
{0: 1, 1: 2, 2: 2, 3: 1, 4: 0, 5: 0}
nx.transitivity(g) # доля наблюдаемых треугольников от числа всевозможных
0.5454545454545454
Выявление сообществ в сети¶
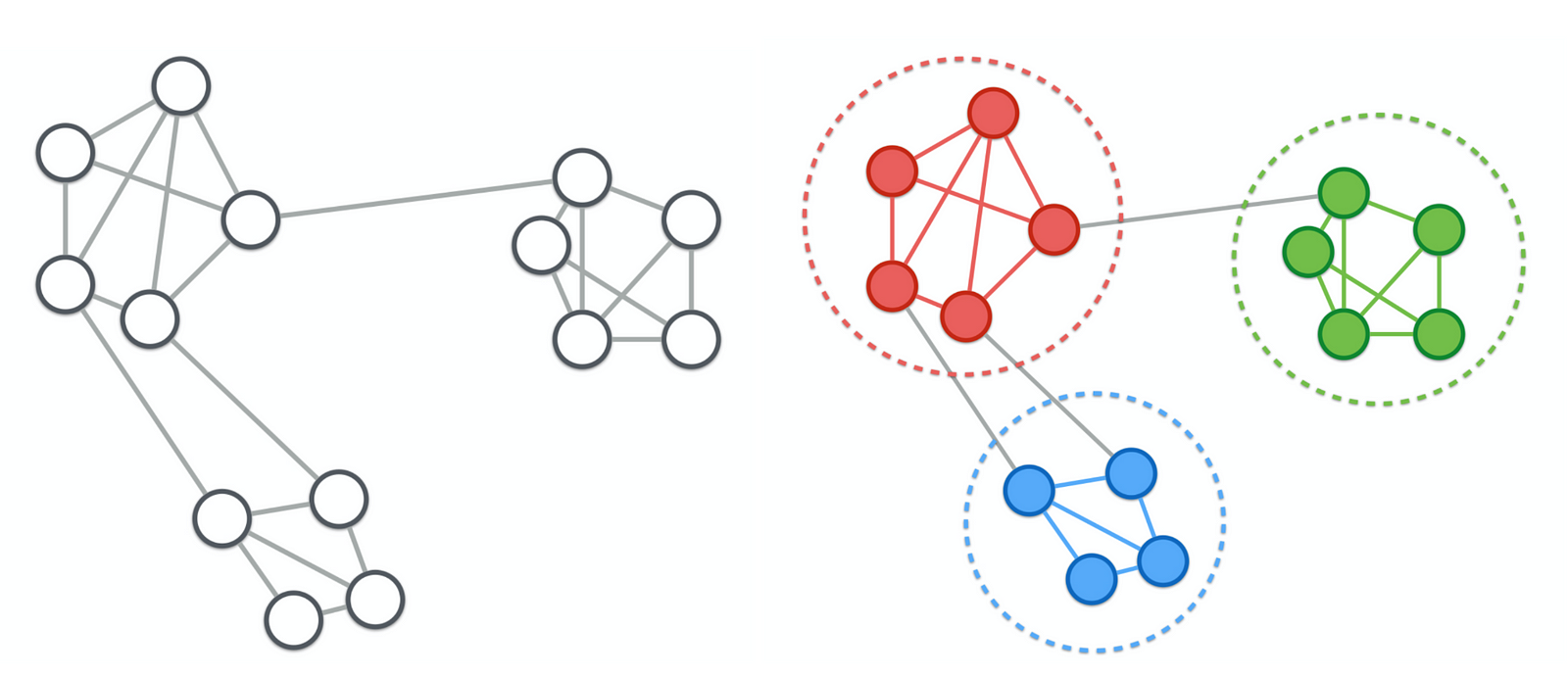
Выявление сообществ в сети¶
Eсли сеть состоит из нескольких множеств узлов с многочисленными и насыщенными внутренними связями и редкими исходящими связями, то говорят, что данная сеть имеет структуру сообществ (community structure).
Примеры:
- Соц-сети: группы по интересам
- Cистемы передачи информации:страницы или сервера разбиваются на группы
- Биологические системы
Выявыление сообществ в сети¶
В настоящее время, нет общепринятого определения сообщества в сетевом анализе
- Очевидно, сообщество, должно быть связным подграфом.
- 'Количество ребер внутри сообщества' > 'число ребер, соединяющих его с остальными узлами сети'
Модели на основе связанности¶
- Клика - максимальный подграф из 3х и более вершин, такой что каждая вершина в нем соединена со всеми остальными
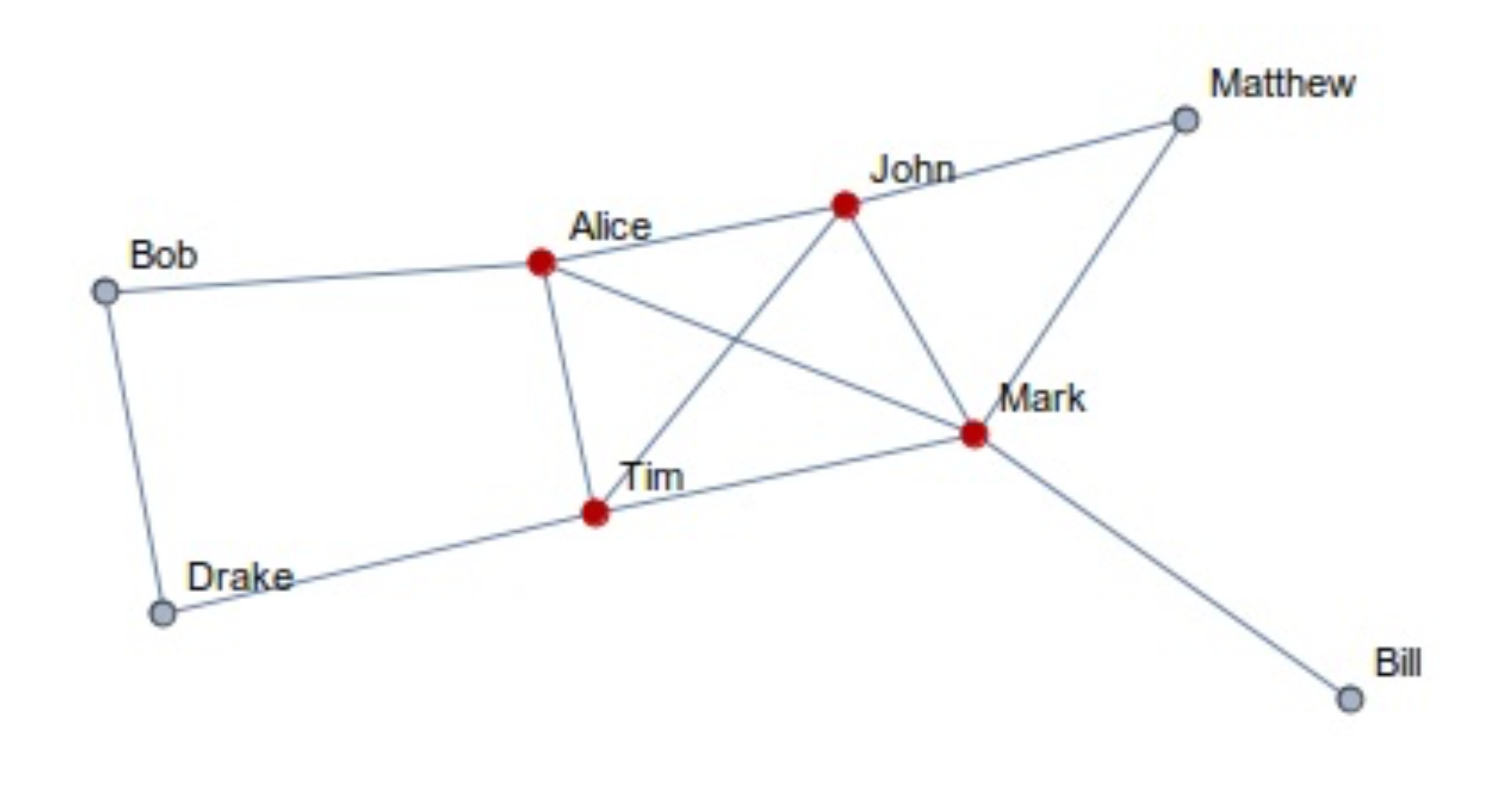
- Слишком строгие требования для сообщества
Релаксация критерия "кликовости"¶
- $n$-клика ($n$-clique) - максимальный подграф, такой что расстояние между каждой парой вершин на исходном графе не превышает $n$
- $n$-клики могут пересекаться
- полученные подграфы могут быть несвязаны
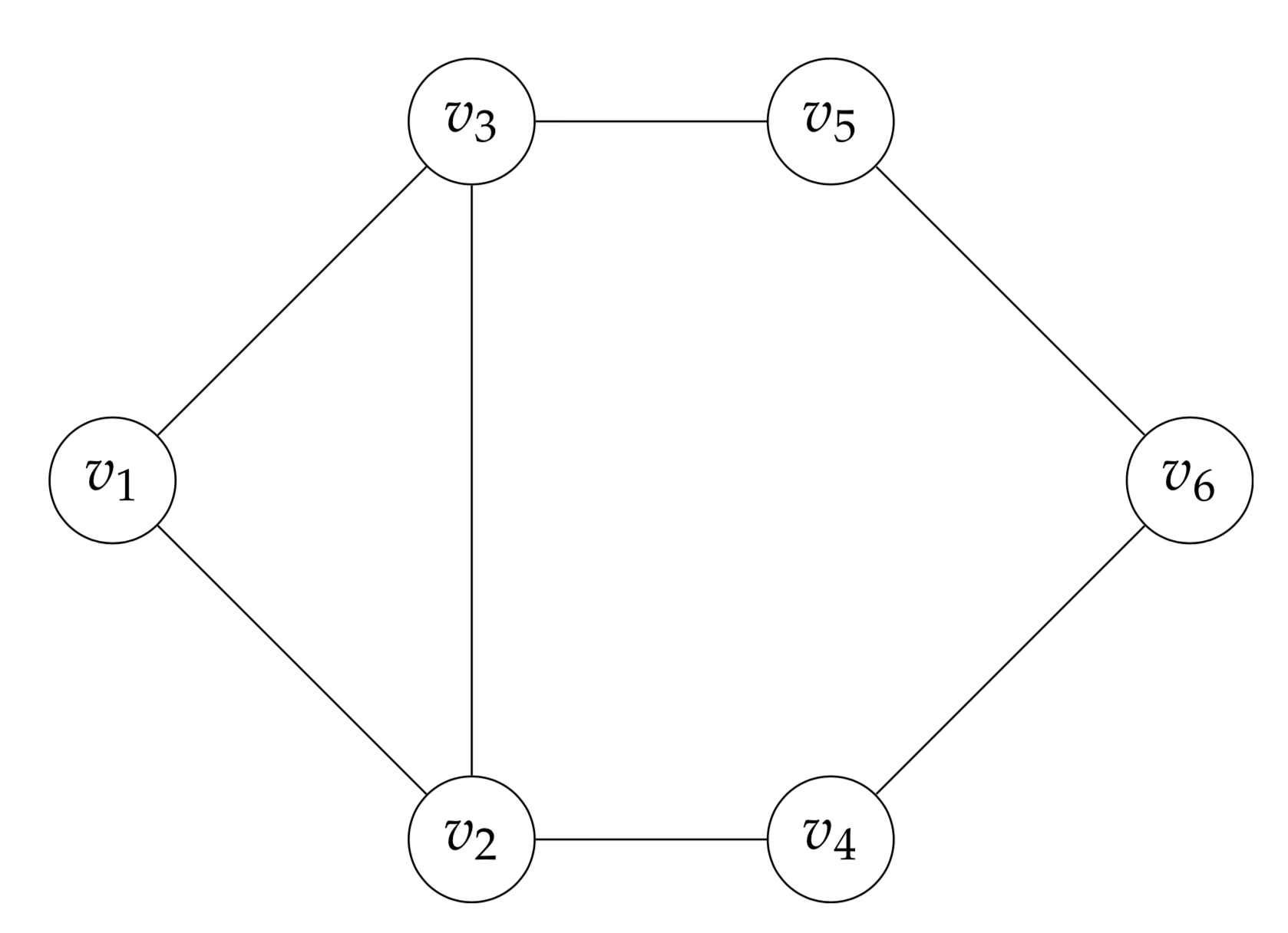
- $(v_1, v_2, v_3, v_4, v_5)$, $(v_2, v_3, v_4, v_5, v_6)$ - $2$-клики
Релаксация критерия "кликовости"¶
- $n$-клан ($n$-clan) - $n$-клика с диаметром не превосходящим $n$

- $(v_2, v_3, v_4, v_5, v_6)$ - $2$-клан
Релаксация критерия "кликовости"¶
- $n$-клуб ($n$-club) - максимальный подграф с диаметром, не превосходящим $n$

- $(v_1, v_2, v_3, v_4)$ - $2$-клуб
Модели, основанные на степени узлов¶
- Узлы должны обладать определенным минимальным числом соседей
k-core¶
- $k$-ядро – это максимальный подграф, в котором каждый узел смежен хотя бы с $k$ другими узлами: все узлы в $k$-ядре обладают степенью не меньше $k$
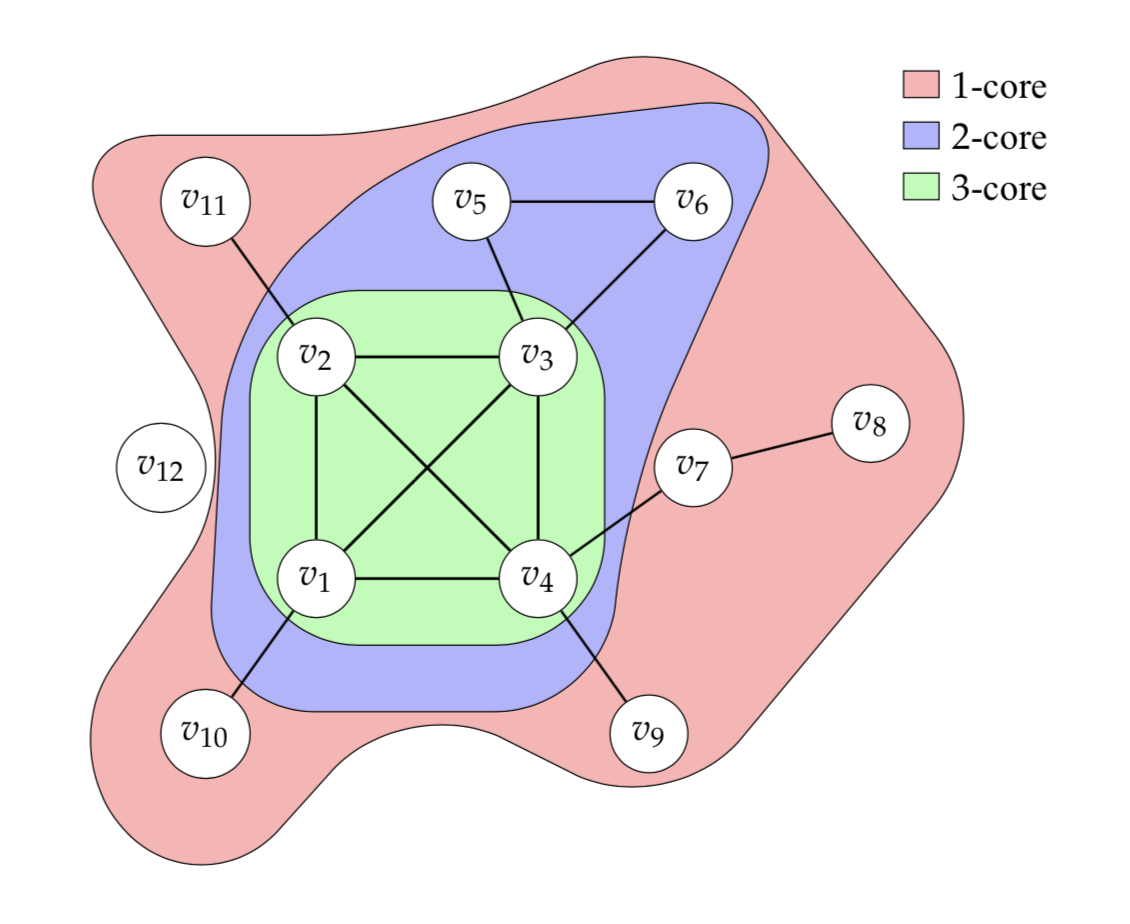
- k-core так же можно использовать для "очистки" сетей от "неинтересных" вершин
Схожесть вершин¶
Понятие "эквивалетности" вершин можно ославить до "схожести" вершин - некоторая мера структурной близости вершин.
Наиболее распространенные практиеские применения мер сходства:
- Выявление сообществ
- Предсказание связей
Примеры мер сходства¶
- $A_{ij}$ - элемент матрицы смежности сети
- $N(v_i)$ - соседи вершины $v_i$
Jaccard Similarity¶
$$ s(v_i, v_j) = \frac{|N(v_i) \cap N(v_j)|}{|N(v_i) \cup N(v_j)|} $$Cosine Similarity¶
$$ s(v_i, v_j) = \frac{\langle A_{i \cdot}, A_{j \cdot} \rangle}{\sqrt{\sum_k A^2_{ik}} \sqrt{\sum_k A^2_{jk}}} $$Correlation¶
$$ s(v_i, v_j) = \frac{\sum_k (A_{ik} - \bar{A}_{i\cdot}) (A_{jk} - \bar{A}_{j\cdot})}{\sqrt{\sum_k (A_{ik} - \bar{A}_{i\cdot})^2} \sqrt{\sum_k (A_{jk} - \bar{A}_{j\cdot})^2}} $$Adamic-Adar Score¶
$$ s(v_i, v_j) = \sum\limits_{z \in N(v_i) \cap N(v_j)} \frac{1}{\log(|N(z)|)} $$Preferential Attachment Score¶
$$ s(v_i, v_j) = |N(v_i)| \cdot |N(v_j)| $$Что можно делать имея попарное сходство между объектами?¶
Иерархическую кластеризацию!
Некоторые специфичные для графов методы¶
Label Propagation¶
- Каждой из вершин приписывается определенное уникальное сообщество
- На каждом шаге вершина принимает ту метку сообщества, которая больше других выражена у соседей
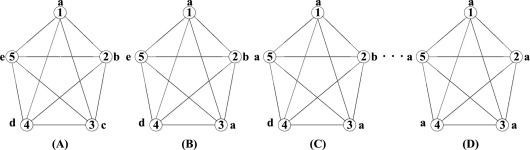
- Какие недостатки вы здесь видите?
Girvan and Newman EdgeBetweenness¶
- Вычислить меру betweenness centrality для каждого ребра
- Найти ребро с наибольшим значением и удалить
- Проверить граф на связанность - присвоить метку связанным компонентам
- Повторять шаги 1-3 пока не будут удалены все ребра
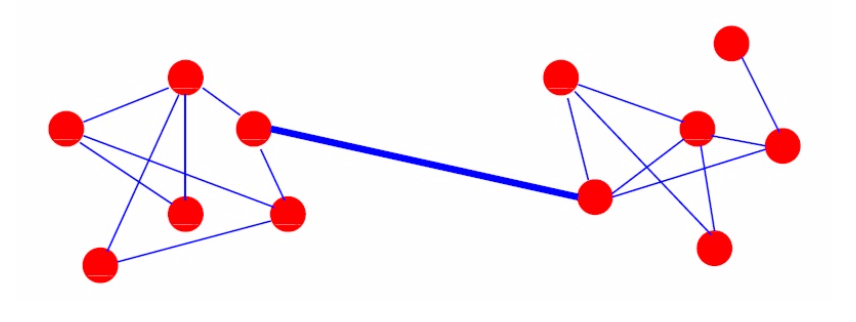
- На выходе - иерархия!
- Как же выбрать количество cообществ?!
Community Scoring Functions¶
Как и в "табличной" кластеризации, качество community detection можно оценить и без ground truth. Для этого считают так называемые scoring functions.
Чего бы нам хотелось получить от выявленного сообщества (разбиения на сообщества):
- Плотности ребер внутри сообщества
- БОльшая доря ребер внутри сообщества относительно ребер, связывающих его с внешним миром
- Высокий коэффициент кластаризации внутри сообщества (относительно среднего по сети)
- Высокая модулярность
В статье можно найти наиболее полный набор так называемых scoring functions
Modularity¶
- Пусть в результате какого-то алгоритма мы получили разбиение на сообщества $C_1,C_2,\dots,C_k$
- Хочется понять насколько это хорошее разбиения
- Сравним раскраску нашего графа на сообщества с той же раскраской, но другого графа с теми же свойствами
nx.draw(g3, pos=m_layout, node_color=mod_labeling)
nx.draw(g3_random, pos=m_layout, node_color=mod_labeling)
Modularity¶
$$ \begin{align} Q & = \frac{1}{2m} \sum\limits_{ij}\left(A_{ij} - P_{ij}\right)\delta(\mathcal{C}_i,\mathcal{C}_j) = \\ & = \frac{1}{2m} \sum\limits_{ij}\left(A_{ij} - \frac{k_i k_j}{2m}\right)\delta(\mathcal{C}_i,\mathcal{C}_j) \end{align}$$где
- $\delta(x, y) = 1$, если $x=y$ и $0$ - иначе
- $P_{ij}$ - вероятность возникновения ребра между вершинами $v_i$ и $v_j$
- $\mathcal{C}_i$ - метка кластера для вершины $v_i$
Какова область значения модулярности?
Возвращаясь к нашему вопросу¶
- Выбираем то разбиение, которое обладает наибольшей модулярностью
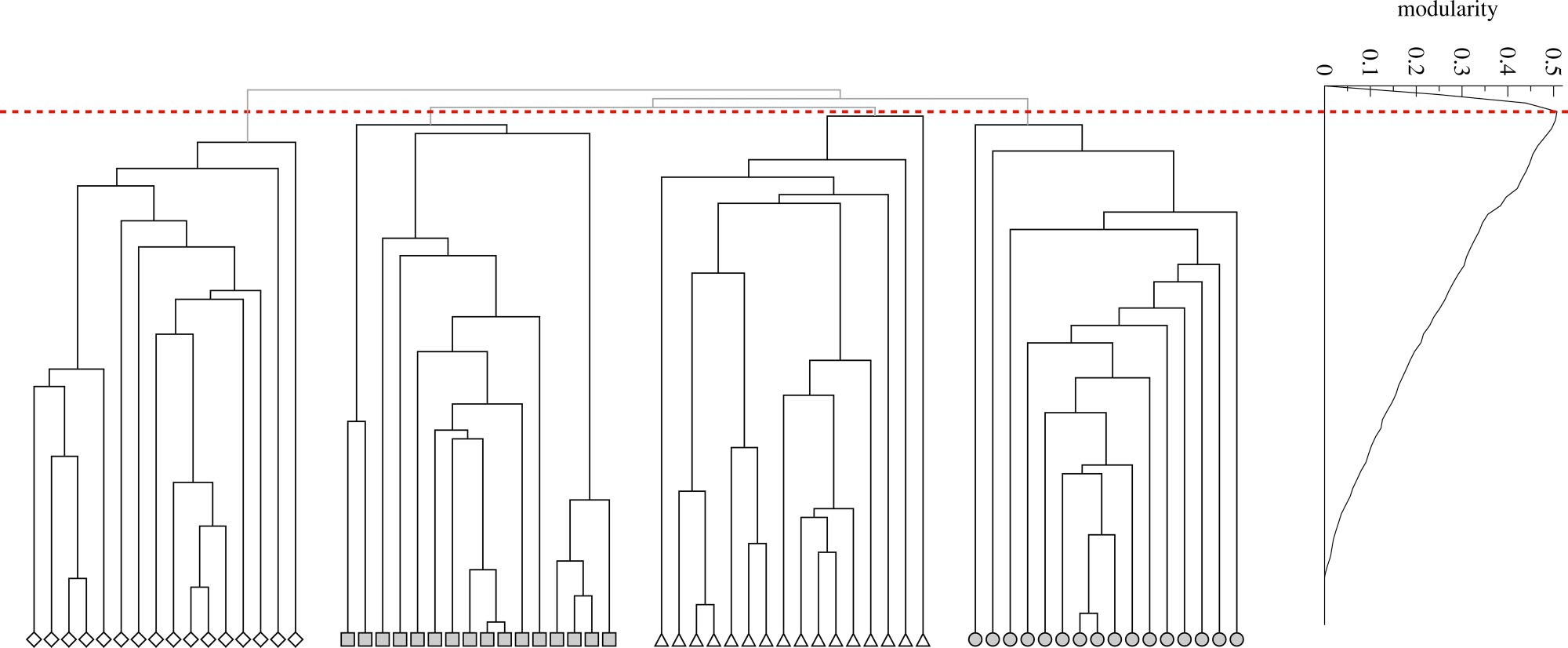
Асортативное смешивание (Assortative Mixing)¶
Асортативное смешивание (Assortative Mixing)¶
- Мера асортативности - это способ измерения гомофилии в сети.
- Насколько схожие по некоторому признаку вершины склонны формировать связи друг с другом
- Можно попытаться ответить на вопросы типа:
- Действительно ли сообщество образовано на основе места проживания
- Насколько сильно похожа зарплата людей в соц-сети
Aсортативность для категориального признака¶
Пусть
- $e_{ij}$ - доля ребер, связывающих вершины типа $i$ и вершины типа $j$
- $a_{i} = \sum_j e_{ij}$ - доля ребер, с вершиной типа $i$ на любом конце
- $b_{j} = \sum_i e_{ij}$ - доля ребер, с вершиной типа $j$ на любом конце
nx.draw_spring(g_test, node_color=list(categ.values()))
nx.assortativity.attribute_assortativity_coefficient(g_test, 'categ')
1.0
nx.draw(g_test, node_color=list(categ.values()))
nx.assortativity.attribute_assortativity_coefficient(g_test, 'categ')
-1.0
Асортативность для числового признака¶
Как не странно, определяется аналогично
Пусть
- $e_{xy}$ - доля ребер, связывающих вершины со значением $x$ и вершины со значением $y$
- $a_{x} = \sum_y e_{xy}$ - доля ребер, с вершиной типа $x$ на любом конце
- $b_{y} = \sum_x e_{xy}$ - доля ребер, с вершиной типа $y$ на любом конце