Методы машинного обучения

 Шестаков Андрей (avshestakov@hse.ru)

Метрические методы

Гипотеза компактности

Метрические методы классификации и регрессии - одни из самых простых моделей.

Они основаны на гипотезе компактности - близким объектам соответствуют близкие ответы. Можно встретить довольно много прецедентов, связанных с этой гипотезой

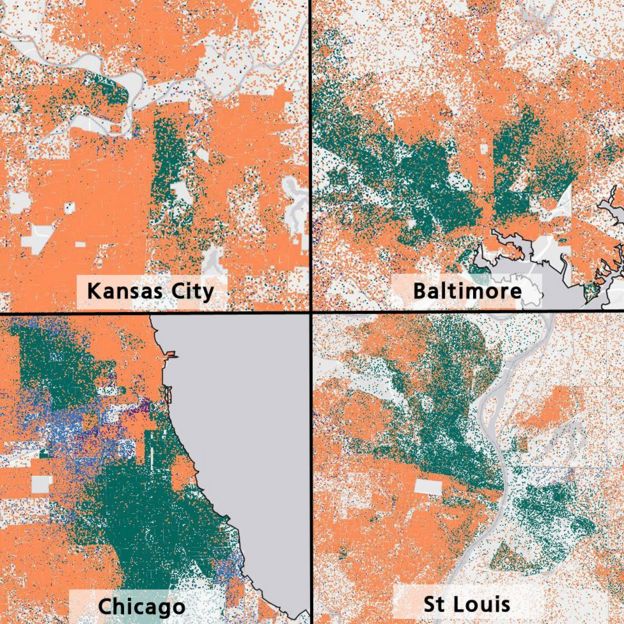
Сегрегация населения в городах

Стоимость жилья в зависимости от расположения

"Похожесть" генов и их функции

Категоризация статей по содержимому

Меры близости

  • Как определить похожие объекты?

  • Необходимо ввести функцию расстояния межну ними

Самые популярные

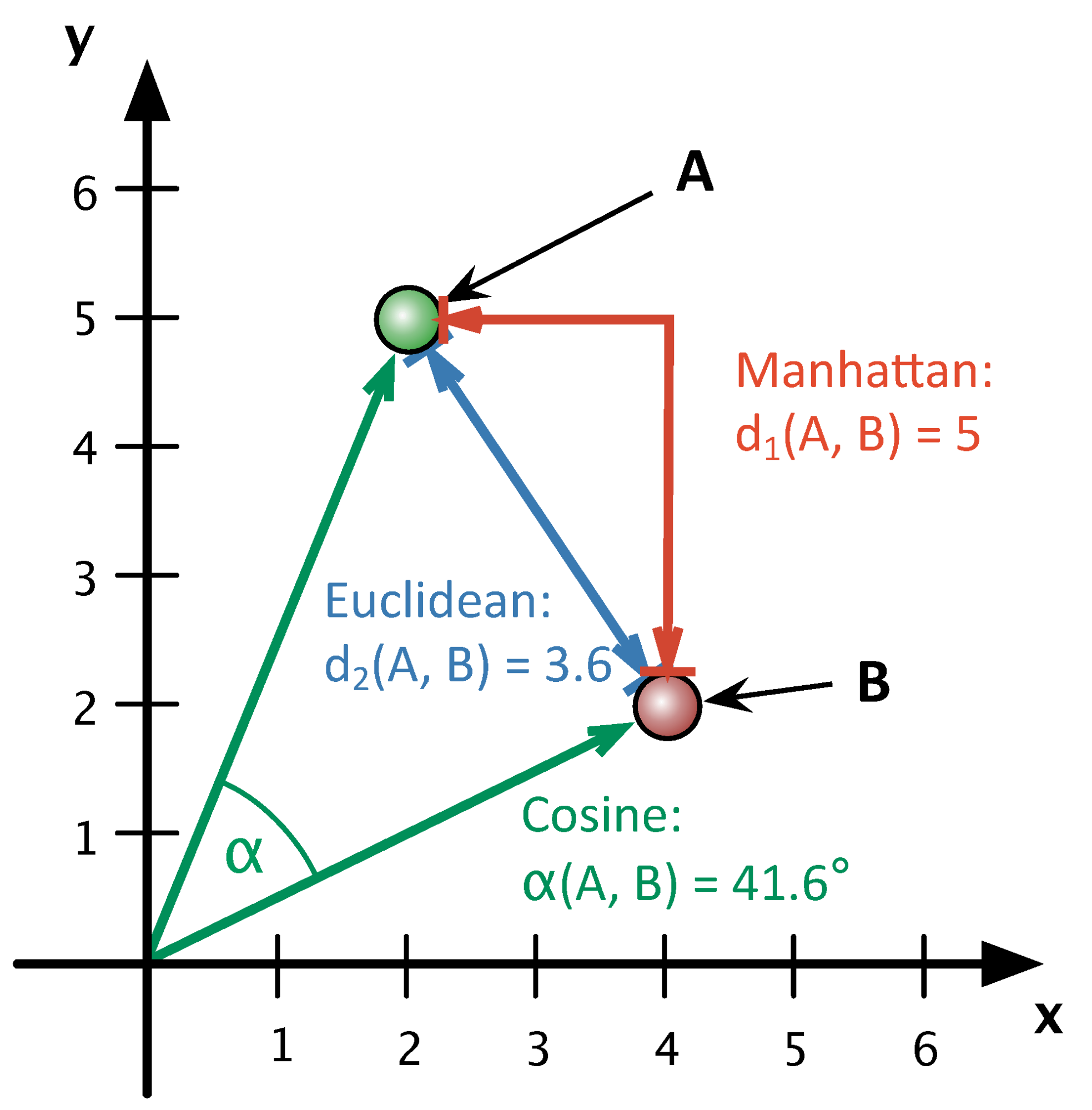
$$ d(a, b) = \sqrt{\sum\limits_{i=1}^{D}(a_i - b_i)^2} \text{: euclidean distance} $$$$ d(a, b) = \sum\limits_{i=1}^{D}|a_i - b_i| \text{: manhattan distance} $$$$ d(a, b) = 1 - \frac{\langle a,b \rangle}{||a||_2\cdot||b||_2} \text{: cosine distance} $$

Illustration

Расстояние на строках

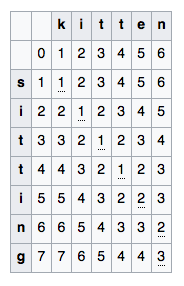
  • Расстояние Левенштейна
    Количество вставок, замен и удалений, которое необходимо сделать, чтобы получить из строки $S_1$ строку $S_2$
\begin{equation} D ( i , j ) = \begin{cases} {\begin{array}{llcl}0,&&&i=0,\ j=0\\i,&&&j=0,\ i>0\\j,&&&i=0,\ j>0\\\min\{\\&D(i,j-1)+1,\\&D(i-1,j)+1,&&j>0,\ i>0\\&D(i-1,j-1)+{\rm {m}}(S_{1}[i],S_{2}[j])\\\}\end{array}}, \end{cases} \end{equation}

где $m(a,b)$ - равно $0$, если $a = b$ и $1$ в ином случае

Близость на бинарных векторах

  • Пусть объект описываеться набором бинарных признаков
    (достиг 18 лет, отслужил в армии, закончил университет, женат)
    • Иван: (1, 0, 1, 0)
    • Геннадий: (1, 1, 0, 1)

  • Расстояние Хэмминга - Hamming distance

    • Количество (доля) несовпавших значений

      $$d(\text{Иван},\text{Геннадий}) = 3 $$

Близость на множествах

  • Пусть объект описываеться набором категорий, слов, тегов
    • Клиент a: {Картофель фри, биг-мак, кофе, маффин}
    • Клиент b: {Картофель фри, сырный соус, чизбургер, кофе, пирожок}
  • Расстояние Жаккара - Jaccard distance:
    • $$d(a,b) = 1 - \frac{|a \cap b|}{|a \cup b|}$$
    • $$d(a,b) = 1 - \frac{2}{7} = \frac{5}{7} $$
  • При правильном представлении данных, можно считать и косинус

Метод ближайших центройдов

Алгоритм МБЦ

  • Вход: обучающая выборка $X=\{\left(x_{1},y_{1}\right),...\left(x_{N},y_{N}\right)\}$ и тестовый объект $\tilde{x}$
  • Пусть
    • $N_{1}$ - количество представителей класса 1
    • $N_{2}$ - количество представителей класса 2
    • итд.
  • Обучение:
    • Вычислим расположение центройдов для классов $c=1,2,...C:$ $$ \mu_{c}=\frac{1}{N_{с}}\sum_{i \in S_c}x_{i} $$
    • Все

  • Классификация:

    • Для тестового объекта $\tilde{x}$ надо найти самый ближайший центройд: $$ c=\arg\min_{i}d(x,\mu_{i}) $$
    • Отнести $x$ к классу ближайшего центройда: $$ \widehat{y}(x)=c $$

  • Примечание - формулы справедливы то евлидового расстояния

Пример для 4х классов

In [5]:
interact(plot_centroid_class)
Out[5]:
<function __main__.plot_centroid_class()>

Обсуждение

  • Как можнь было бы посчитать "вероятность" принадлежности к класса?
  • Как можно адаптировать этот подход для регрессии?

Метод k ближайших соседей (KNN)

Метод k ближайших соседей (для классификации)

Вход: Обучающая выборка $X=(x_i,y_i)$, мера близости $d(\cdot, \cdot)$ и тестовый объект $\tilde{x}$

Найти $k$ ближайших объекта в $X$ c помощью $d(\tilde{x},\cdot)$

  • (классификация) вернуть наиболее частую метку класса
  • (вероятность) вернуть долю объектов каждого из классов среди ближайших соседей
In [8]:
plt.scatter(X_moons[:,0], X_moons[:,1], c=y_moons, cmap=plt.cm.Spectral)
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
Out[8]:
Text(0,0.5,'$x_2$')
In [10]:
interact(plot_knn_class, k=IntSlider(min=1, max=10, value=1))
Out[10]:
<function __main__.plot_knn_class(k=1, prob=False)>

Метод k ближайших соседей (для регрессии)

  • Найти $k$ ближайших объектов из обучающей выборки для $\tilde{x}$
  • Усреднить ответы блишайших соседей и присвоить результат $\tilde{x}$
In [12]:
plt.plot(x_true, y_true, c='g', label='$f(x)$')
plt.scatter(x, y, label='actual data')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=2)
Out[12]:
<matplotlib.legend.Legend at 0x1a1c0f4780>
In [14]:
plot_linreg()
In [16]:
interact(plot_knn, k=IntSlider(min=1, max=10, value=1))
Out[16]:
<function __main__.plot_knn(k=1)>

Параметры vs Гиперпараметры алгоритмов

Параметры vs Гиперпараметры

При работе с моделями следует различать понятия Параметр и Гипер-параметр.

  • Параметр - составляющая модели, которая определяется в процессе обучения самой моделью
    • Веса коэффициентов в модели линейной регрессии
  • Гиперпараметр - составляющая модели, которая задается перед началом обучения. Может регулировать некоторые свойства модели или ее сложность
    • Коэффициент регуляризации в линейной регрессии

Как дела обстоят у kNN?

  • kNN - непараметрическая модель!
  • kNN - ленивая модель (lazy learning)!

Нормализация признаков

  • Шкалы признаков влияют на рассчет расстояния
  • Разные масштабы шкал - разный вклад признаков
  • Стандартные способы нормализации:
    • z-scoring: $$x_{j}'=\frac{x_{j}-\mu_{j}}{\sigma_{j}}$$
    • интервальное шкалирование: $$x_{j}'=\frac{x_{j}-L_{j}}{U_{j}-L_{j}}$$

где $x_j$ - $j$-ый признак
$\mu_{j}$ - среднее значение признака $x_j$,
$\sigma_{j}$ - его стандартное отклонение
$L_{j}$ и $U_{j}$ - верхняя и нижняя "границы"

Взвешенный kNN

Взвешенный kNN

Взвешенный kNN

У каждого ближайшего соседа возникает "вес" важности в предсказании. Пусть $(j)$ показывает порядок ближайшего соседа, тогда:

  • (регрессия) вернуть среднее взвешенное значение* $$\hat{y} = \frac{\sum\limits_{j=1}^k w_{(j)} y_{(j)}}{\sum\limits_{j=1}^k w_{(j)}}$$
  • (классификация) вернуть наиболее частую метку класса c учетом веса $$\hat{y} = \arg \max\limits_{с}\sum\limits_{j=1}^k w_{(j)} [y_{(j)} == с] $$

Варианты весов

  • $w_{(j)}=\alpha^{k},\quad\alpha\in(0,1)$
  • $w_{(j)} = \frac{k - j + 1}{k}$
  • $w_{(j)} = 1/d(\tilde{x},x_{(j)})$
In [18]:
interact(plot_knn_dist, k=IntSlider(min=1, max=10, value=1))
Out[18]:
<function __main__.plot_knn_dist(k=1)>
In [19]:
interact(plot_knn_class_kernel, k=IntSlider(min=1, max=10, value=1))
Out[19]:
<function __main__.plot_knn_class_kernel(k=1, prob=False)>

Меры качества классификации

Меры качества классификации

  • Как правило, классификаторы выдают не просто предсказанную метку класса, но и степень уверенности в ней
  • Основные меры качества
    • Accuracy
    • Precision, Recall, F-measure
    • ROC-AUC, PR-AUC Gini-index, Model-lift
    • Log-loss

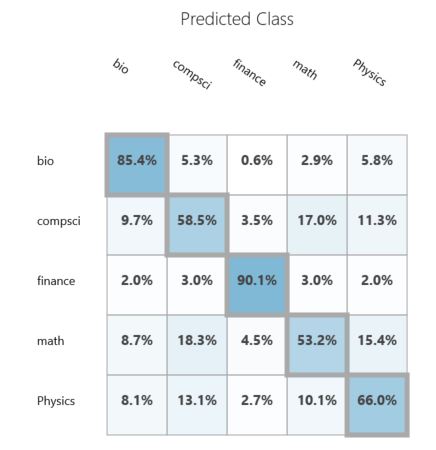
Матрица перемешивания

Матрица перемешивания $M=\{m_{ij}\}_{i,j=1}^{C}$ показывает количество объектов класса $с_{i}$, которые были отнесены классификатором к классу $с_{j}$.

Матрица перемешивания (2 класса)

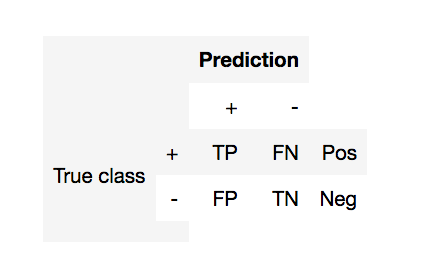
  • TP (true positive) - Верное предсказание (+1)
  • FP (false positive) - Ошибка первого рода (ложная тревога)
  • FN (false negative) - Ошибка второго рода (пропуск цели)
  • TN (true negative) - Верное предсказание (-1)
  • Pos (Neg) - Общее количество +1 и -1

Меры на основе матрицы перемешивания

  • $ \text{accuracy} = \frac{TP + TN}{Pos+Neg}$
  • $ \text{error rate} = 1 -\text{accuracy}$
  • $ \text{recall} =\frac{TP}{TP + FN} = \frac{TP}{Pos}$ - (полнота)
  • $ \text{precision} =\frac{TP}{TP + FP}$ - (точность)
  • $ \text{F}_\beta \text{-score} = \frac{1+\beta^2}{\frac{1}{Recall} + \frac{1}{\beta^2 Precision}} = (1 + \beta^2) \cdot \frac{\mathrm{precision} \cdot \mathrm{recall}}{(\beta^2 \cdot \mathrm{precision}) + \mathrm{recall}}$
    • почему не среднее или максимум?
  • Можно ли посчитать эти меры для многоклассовой классификации?
In [21]:
fig = interact(demo_fscore, beta=FloatSlider(min=0.1, max=5, step=0.3, value=1))

Меры качества на основе уверенности классификатора

ROC кривая

  • Выбор порога классификации - отдельная большая задача
  • Можно ли как-то обойтись без него и сравнить неколько моделей?
  • ROC кривая - показывает зависимость между TPR (верным предсказанием) и FPR (ложным срабатыванием)

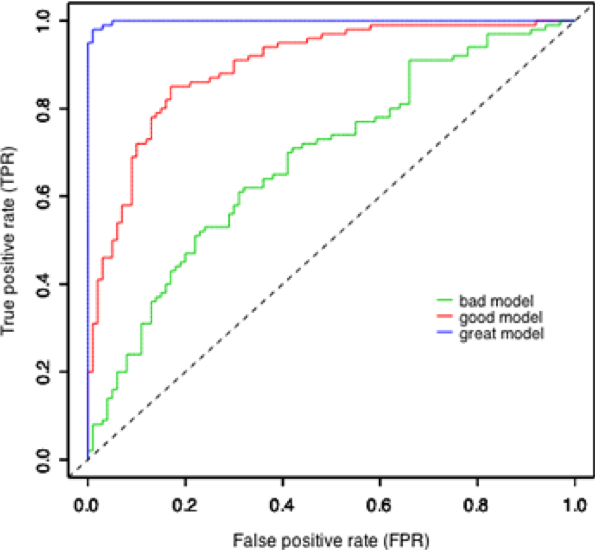
ROC кривая

  • Классификатор $a(x)$ возвращает степень принадлежности к классу "+1" - score(x).
  • Упорядочим объекты по убыванию score(x)
  • Смотрим сверху вниз
    • Если объект принадлежит классу "+1" - сдвиг вверх на $1/Pos$
    • Если объект принадлежит классу "-1" - сдвиг вправо на $1/Neg$

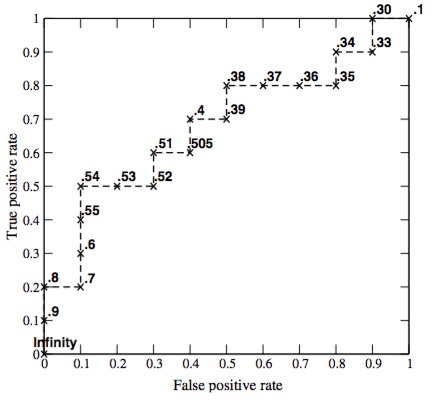
Как сравнивать ROC-кривые?

ROC-AUC

  • Площадь под ROC кривой

  • AUC$\in[0,1]$

    • AUC = 0.5 - случайный классификатора
    • AUC = 1 - идеальный классификатор

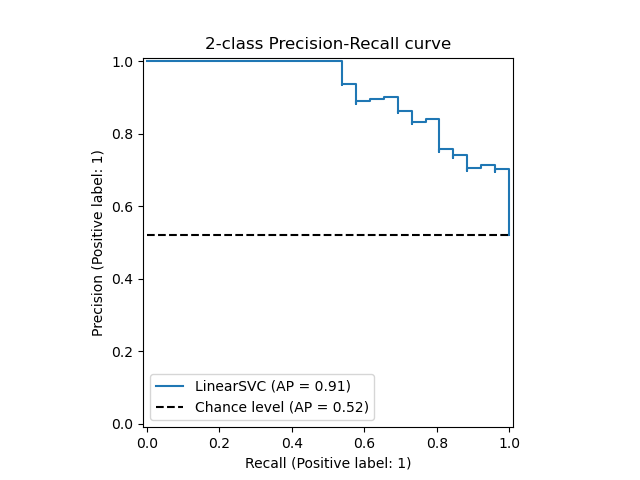
Precision-Recall Кривая

  • Строится аналогичным образом, но по осям Precision и Recall для разных порогов