Методы машинного обучения

 Шестаков Андрей (avshestakov@hse.ru)

Линейные модели

Линейные модели

  • Линейная регрессия
  • Logit и Probit регрессия
  • Метод опорных векторов (Support Vector Machine)
  • *Обобщенные линейные модели (GLM)
  • *LDA (Linear Discriminant Analysis)

Вспоминаем примеры

  • Эти признаки очевидно как-то влияют на цену ($f: X \rightarrow Y$)
  • Составим модель, которая будет принимать на входе эти признаки: $$a(x) = a(total\_area, nmbr\_of\_bedrooms, house\_age) = \hat{y}$$
  • Пусть она будет иметь линейный вид: $$a(x) = w_0 + w_1\cdot total\_area + w_2 \cdot nmbr\_of\_bedrooms + w_3 \cdot house\_age$$
  • Обучение - найти коэффициенты $w_0,\dots, w_3$, минимизирующие ошибку на обучающей выборке

Вспоминаем примеры 2

Отзыв Тональность
Преподаватели сильные, отвечали на вопросы оперативно (по большей части), что приятно — даже в выходные и поздно вечером. +1
Здорово, что были трансляции по доп.материалу (обработка текстов). Хотелось бы побольше такого. От Петра много лайфхаков по обработке текста узнала. Спасибо ему! +1
Очень жаль, что мало рассказали про Deep Learning -1
  • Как будет выглядеть простейшая линейная модель в данном случае?

Исторические и практические нюансы

  • К линейным моделям (как и со многими методами МО) можно относится по-разному:
    • В Эконометрике (Прикладной статистике и тп) при изучении линейных моделей обращают особое внимание на различные статистические характеристики данных, которые подаются на вход, харакретистики самой модели (значимость коэффициентов), ее интерпретацию
    • В Машинном обучении на это обращают меньше внимания...
  • Мы с вами будем где-то между, я надеюсь..

Линейная регрессия

In [5]:
df_auto.plot(x='mileage', y='price', kind='scatter', s=120)
Out[5]:
<matplotlib.axes._subplots.AxesSubplot at 0x11d75f710>

Постановка задачи

Наша задача, выявить линейную зависимость между признаками в $X \in \mathbb{R}^m$ и значениями в $y \in \mathbb{R}$: $$\hat{y}^{(i)} = \beta_0 + \beta_1x^{(i)}_1 + \dots = \mathbf{\beta^T X}$$ То есть необходимо оценить коэффициенты $\beta_i$.

Для случая предыдущего слайда уравнение выглядит так:

$$ \hat{y}_{price} = \beta_0 + \beta_1 x_{mileage} $$
  • $\beta_0$ еще называют "свободным" коэффициентом (intersept)
  • $\beta_1$, $\beta_2$ и тп - это коэффициенты при признаках (slopes)

Постановка задачи

  • Как понять, хорошие ли коэффициенты или плохие?
  • Введем квадратичную функцию потерь $L(\cdot)$ и будем искать такие $\beta_i$, чтобы она была минимальной
$$ L(\beta_0,\beta_1,\dots) = \frac{1}{2n}\sum^{n}_{i=1}(\hat{y}^{(i)} - y^{(i)})^2 = \frac{1}{2n}\sum^{n}_{i=1}(\beta_0 + \beta_1x^{(i)}_1 + \dots - y^{(i)})^2 \rightarrow \min\limits_{\beta_i} $$

Можно получить решение аналитически

Считаем частные производные по $\beta_0$, $\beta_1$, приравниваем к $0$, получаем нужные значения коэффициентов:

$$ \frac{\partial L}{\partial \beta_0} = \frac{1}{n}\sum^{n}_{i=1}(\beta_0 + \beta_1x^{(i)}_1 - y^{(i)}) = 0$$$$ \frac{\partial L}{\partial \beta_1} = \frac{1}{n}\sum^{n}_{i=1}(\beta_0 + \beta_1x^{(i)}_1 - y^{(i)})x_1^{(i)} = 0$$

Можно получить решение аналитически

Можно обобщить на большее количество признаков и перевести в матричный вид:

$$ X^\top X\beta - X^\top y = 0 \quad \Leftrightarrow \quad \beta = (X^\top X)^{-1} X^\top y \quad\text{(Normal Equation)}$$

Почему так делать не стоит?

  • Расчет обратной матрицы - дорогая и не совсем устойчивая операция (хотя бы потому что не у всякой матрицы есть обратная)
  • Лучше будет воспользоваться методами оптимизации
In [10]:
sq_loss_demo()

Tiny Refresher

Производная функции $f(x)$ в точке $f(x_0)$: $$ f'(x_0) = \lim\limits_{h \rightarrow 0}\frac{f(x_0+h) - f(x_0)}{h}$$

Производная равна углу наклона касательной в точке $x_0$

In [12]:
interact(deriv_demo, h=FloatSlider(min=0.0001, max=2, step=0.005), x0=FloatSlider(min=1, max=15, step=.2))
Out[12]:
<function __main__.deriv_demo(h, x0)>

Tiny Refresher

  • Производные помогают находить эксремумы функций
  • Если точка $x_0$ - экстремум функции, и в ней существует производная то $f'(x_0) = 0$

Tiny Refresher

  • В многомерном случае все обобщается и переходят к производным по направлению и градиенту: $$ f'_v(x_0) = \lim\limits_{h \rightarrow 0}\frac{f(x_0+hv) - f(x_0)}{h} = \frac{d}{dh}f(x_{0,1} + hv_1, \dots, x_{0,d} + hv_d) \rvert_{h=0}, \quad ||v|| = 1 \quad \text{Производная по направлению}$$
$$ \frac{ \partial f(x_1,x_2,\dots,x_d)}{\partial x_i} = \lim\limits_{h \rightarrow 0}\frac{f(x_1, x_2, \dots, x_i + h, \dots, x_d) - f(x_1, x_2, \dots, x_i, \dots, x_d)}{h} \quad \text{Частная производная}$$$$ \nabla f = \left(\frac{\partial f}{\partial x_i}\right),\quad i=1\dots d \quad \text{Градиент = вектор частных производных}$$

Tiny Refresher

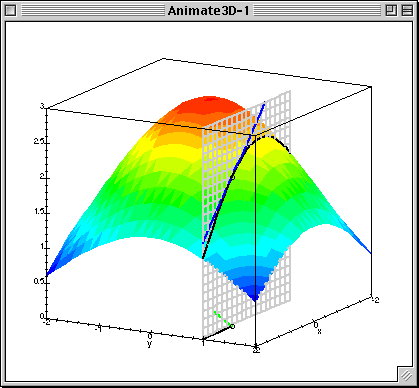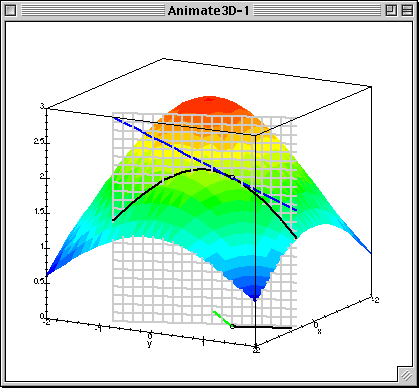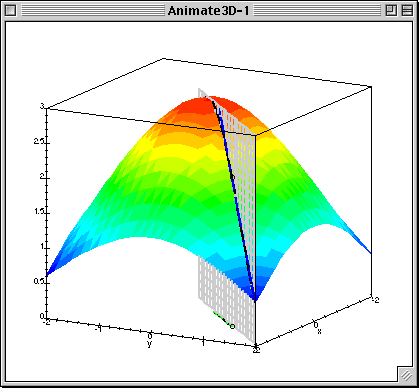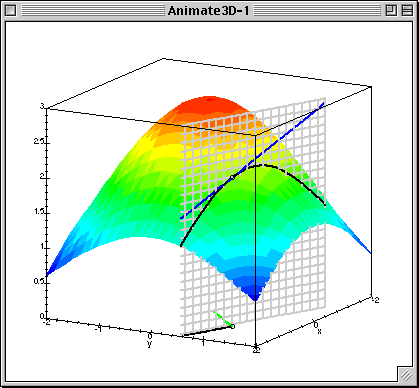
  • Произвольная по направлению максимальна, если направление совпадает с градиентом.
  • Градиент — направление наискорейшего роста функции
  • Антиградиент — направление наискорейшего убывания функции

Градиентный спуск

$$ L(\beta_0, \beta_1) = \frac{1}{2n}\sum_{i=1}^n(\beta_0 + \beta_1x_1^{(i)} - y^{(i)})^2$$

  • Предположим мы выбрали какое-то начальное приближение $(\hat{\beta_0}, \hat{\beta_1})$
  • Его можно постараться улучшить - надо двигаться в сторону наискорейшего убывания функции (Антиградиента!)
In [14]:
sq_loss_demo()

Посчитаем, чему равен градиент функции потерь $L(\beta_0, \beta_1):$ $$ \frac{\partial L}{\partial \beta_0} = \frac{1}{n}\sum^{n}_{i=1}(\beta_0 + \beta_1x^{(i)}_1 - y^{(i)})$$ $$ \frac{\partial L}{\partial \beta_1} = \frac{1}{n}\sum^{n}_{i=1}(\beta_0 + \beta_1x^{(i)}_1 - y^{(i)})x_1^{(i)}$$

Иногда проще это записать в виде матриц: $$ \frac{\partial L}{\partial \beta} = \frac{1}{n} X^\top(X\beta - y)$$

Метод градиентного спуска заключается в итеративном и одновременном(!!!) обновлении значений $\beta$ в направлении, противоположному градиенту: $$ \beta := \beta - \alpha\frac{\partial L}{\partial \beta}$$

  • $\alpha$ - скорость спуска

Псевдокод алгоритма

{python}
1.function gd(X, alpha, epsilon):

2.  initialise beta 

3.  do: 

4.      Beta = new_beta

5.      new_Beta = Beta - alpha*grad(X, beta)

6.  until dist(new_beta, beta) < epsilon

7.  return beta
In [15]:
sq_loss_demo()
grad_demo(iters=105, alpha=0.08)

Нюансы

  • Как ставить $\alpha$?
  • Шкала признаков играет роль
  • Локальные экстремумы*
  • Много данных

Стохастический градиентный спуск

{python}
1.function sgd(X, alpha, epsilon):

2.  initialise beta 

3.  do: 

4.        X = shuffle(X)

5.        for x in X:

6.            Beta = new_beta

7.            new_Beta = Beta - alpha*grad(x, beta)

8.  until dist(new_beta, beta) < epsilon

9.  return beta
In [16]:
stoch_grad_demo(iters=105, alpha=0.08)

Вариации градиентного спуска

  • Стохастический градиентрый спуск (!)
  • Градиентный спуск с адаптивной скоростью $\alpha$
  • Корректировка на импульс
  • ...

Обзор методов 1, обзор 2

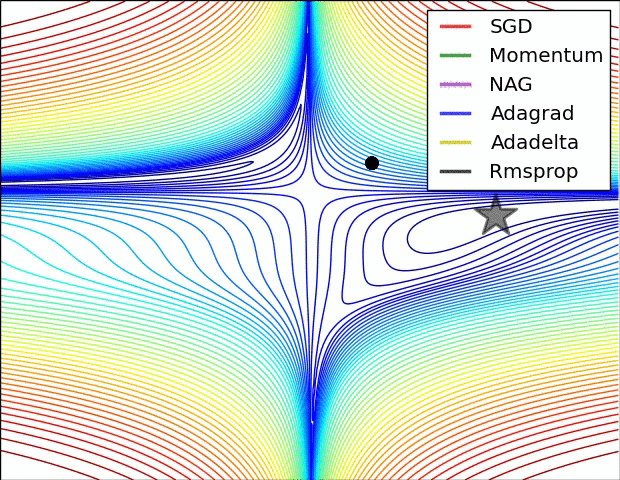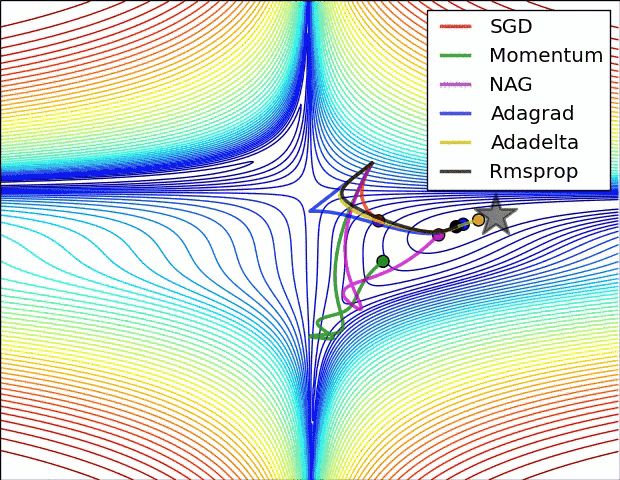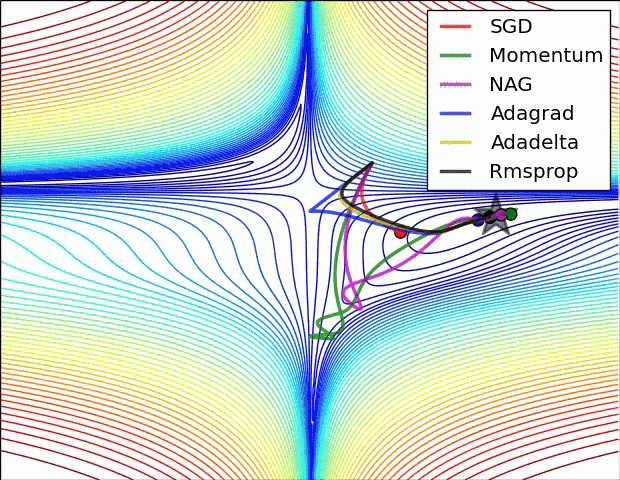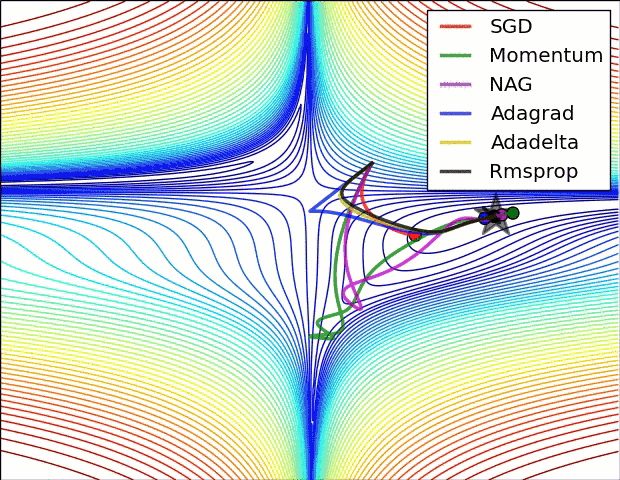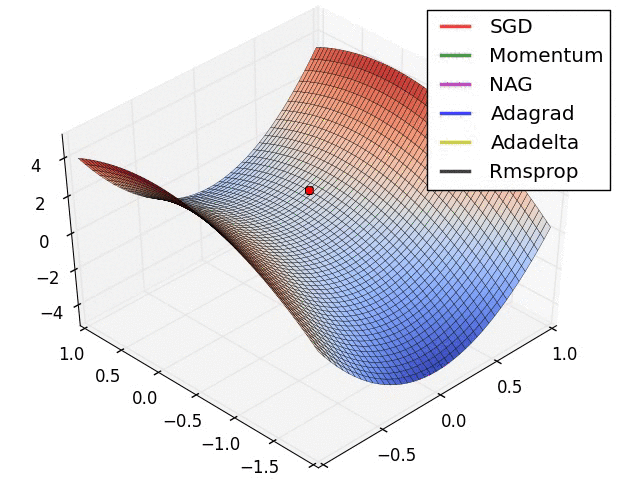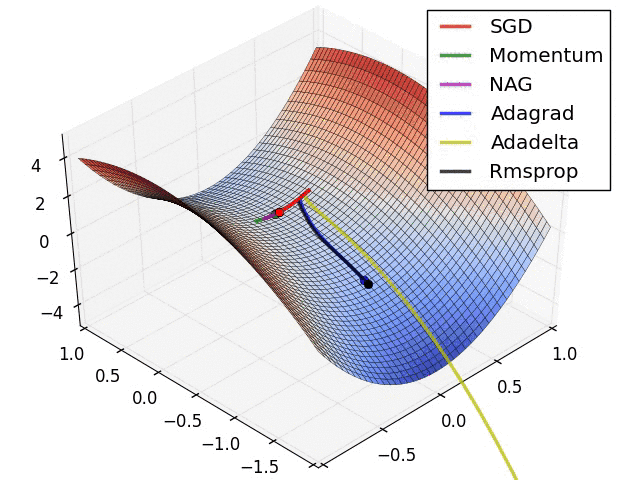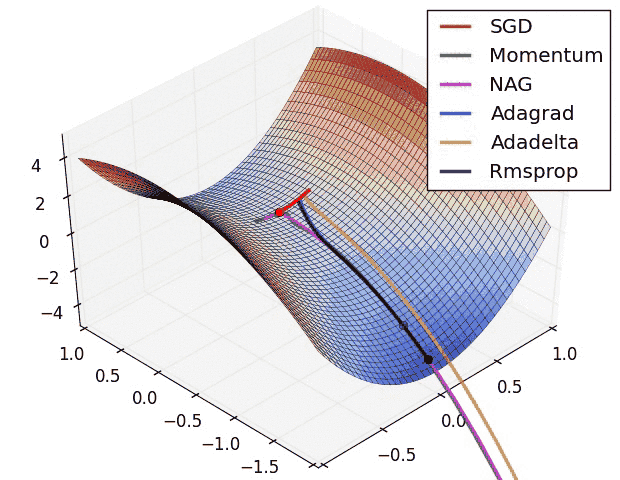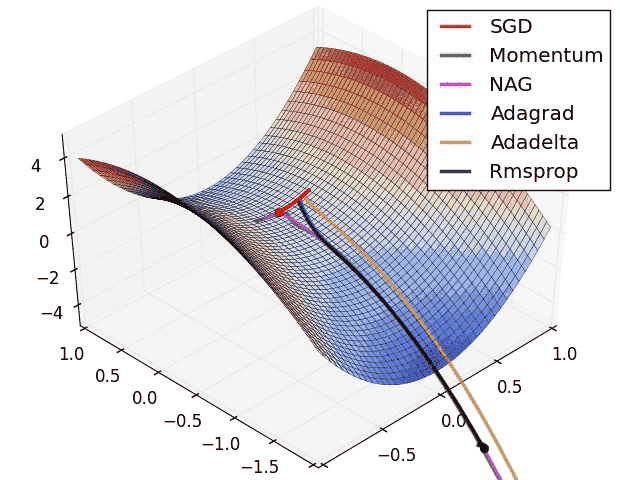Основные факторы

Переобучение\недообучение

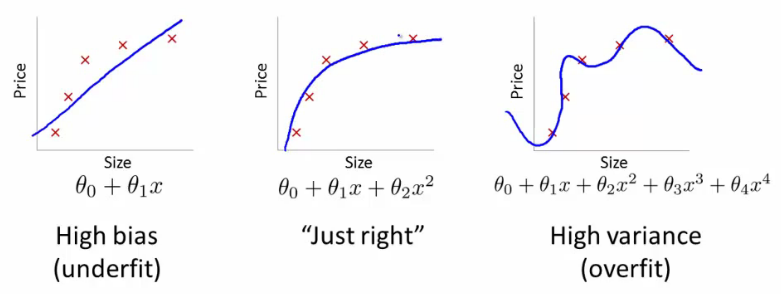
[Andrew's Ng Machine Learning Class - Stanford]

Мультиколлинеарность

Мультиколлинеарность - эффект при котором, подмножество предикторов являются (почти) линейно зависимыми (для пары признаковы коэффициент корреляции по модулю близок к 1). Из-за этого:

  • Зависимость $y = \beta_0 + \beta_1x_1 + \beta_2x_2$ перестаёт быть одназначной

С этим эффектом можно бороться несколькими способами

  • Последовательно добавлять переменные в модель
  • Исключать коррелируемые предикторы

Регуляризация

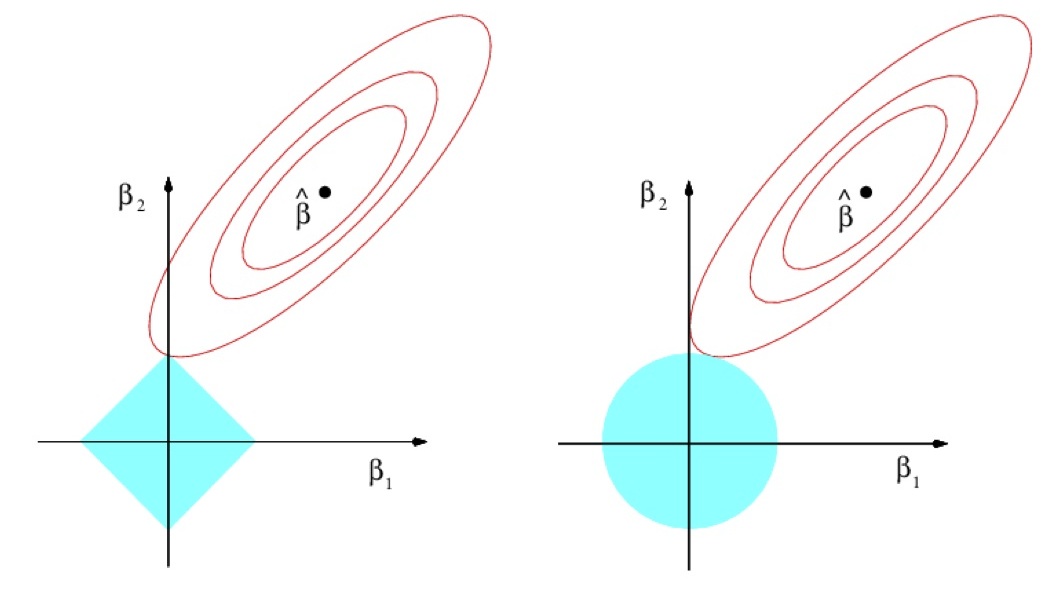
В обоих случаях может помочь регуляризация - добавление штрафного слагаемого за сложность модели в функцию потерь. В случае линейной регрессии было: $$ L(\beta_0,\beta_1,\dots) = \frac{1}{2n}\sum^{n}_{i=1}(a(x^{(i)}) - y^{(i)})^2 $$ Стало (Ridge Regularization) $$ L(\beta_0,\beta_1,\dots) = \frac{1}{2n}\left[ \sum^{n}_{i=1}(a(x^{(i)}) - y^{(i)})^2\right] + \frac{1}{C}\sum_{j=1}^{m}\beta_j^2$$ или (Lasso Regularization) $$ L(\beta_0,\beta_1,\dots) = \frac{1}{2n}\left[ \sum^{n}_{i=1}(a(x^{(i)}) - y^{(i)})^2\right] + \frac{1}{C}\sum_{j=1}^{m}|\beta_j| $$

Природа зависимости

Далеко не всегда переменные зависят друг от друга именно в том виде, в котором они даны. Никто не запрещает зависимость вида $$\log(y) = \beta_0 + \beta_1\log(x_1)$$ или $$y = \beta_0 + \beta_1\frac{1}{x_1}$$ или $$y = \beta_0 + \beta_1\log(x_1)$$ или $$y = \beta_0 + \beta_1 x_1^2 + \beta_2 x_2^2 + \beta_3 x_1x_2 $$ и т.д.

Не смотря на то, что могут возникать какие-то нелинейные функции - всё это сводится к линейной регрессии (например, о втором пункте, произведите замену $z_1 = \frac{1}{x_1}$)

Логистическая регрессия

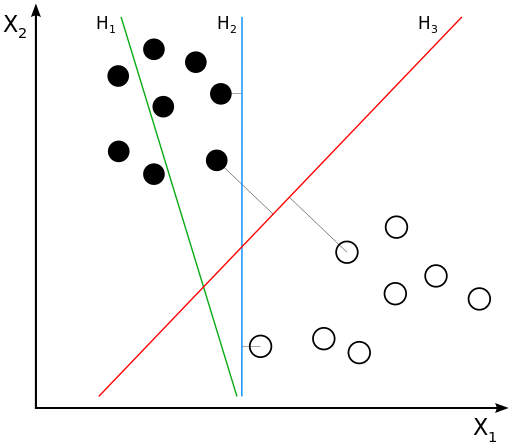
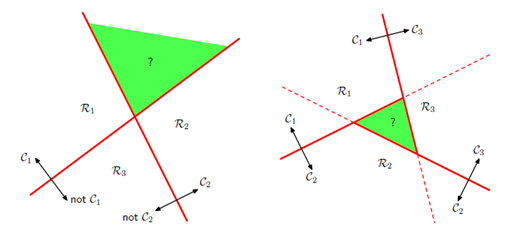
Нам надо найти уравнение прямой (гиперплоскости), которая бы могла разделить два класса ($H_2$ и $H_3$ подходят). В данном случае, уравнение прямой задаётся как: $$g(x) = w_0 + w_1x_1 + w_2x_2 = \langle w, x \rangle + w_0 = w^\top x + w_0$$

  • Если $g(x^*) > 0$, то $y^* = \text{'черный'} = +1$
  • Если $g(x^*) < 0$, то $y^* = \text{'белый'} = -1$
  • Если $g(x^*) = 0$, то мы находимся на линии

Перед тем как мы начнем, рассмотрим функцию $$\sigma(z) = \frac{1}{1 + exp{(-z)}},$$она называется сигмойда.

In [ ]:
def sigmoid(z): 
    return 1./(1+np.exp(-z))
demo_sigmoid()

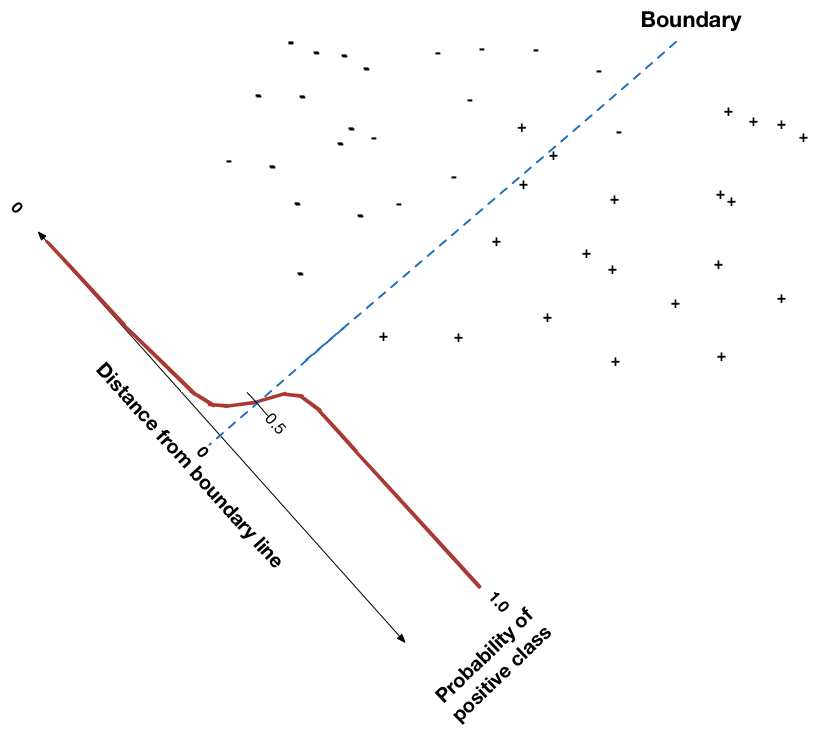
Постановка задачи

Будем требовать, чтобы алгоритм возвращал вероятность класса $y=+1$: $$h(x,w) = p(y=+1|x,w) = \sigma(g(x))$$

Выпишем функцию правдоподобия $$ \mathcal{L}(w) = \prod_i^n h(x^{(i)},w)^{[y^{(i)} = +1]} (1 - h(x^{(i)},w))^{[y^{(i)} = -1]} \rightarrow \max_w$$ $$ -\log{\mathcal{L}(w)} = - \sum_i^n [y^{(i)} = +1]\cdot\log{(h(x^{(i)},w))} + {[y^{(i)} = -1]}\cdot\log{(1-h(x^{(i)},w))} \rightarrow \min_w$$ $$L(w) = \log{\mathcal{L}(w)} \rightarrow \min_w $$

In [ ]:
logloss_demo()

Рассмотрим объекты со следующими признаками:

x1 x2
0 1
1 0
1 1
2 2
2 3
3 2

Определите к какому классу относятся наблюдения, если вектор параметров имеет вид $(w_0 = -0.3 , w_1 = 0.1, w_2 = 0.1)$

In [ ]:
X = np.array([[0,1],[1,0],[1,1],[2,2],[2,3],[3,2]]) 
w = np.array([.1, .1])
w0 = -.3

Другая постановка

Вспоминаем

$$g(x) = w_0 + w_1x_1 + w_2x_2 = \langle w, x \rangle + w_0 = w^\top x + w_0$$
  • Если $g(x^*) > 0$, то $y^* = \text{'черный'} = +1$
  • Если $g(x^*) < 0$, то $y^* = \text{'белый'} = -1$
  • Если $g(x^*) = 0$, то мы находимся на линии
  • т.е. решающее правило: $y^* = sign(g(x^*))$

Величину $M_i = y^{(i)} \cdot g(x^{(i)})$ называют отступом(margin)

Если для какого-то объекта $M_i \geq 0$, то его классификация выполнена успешно.

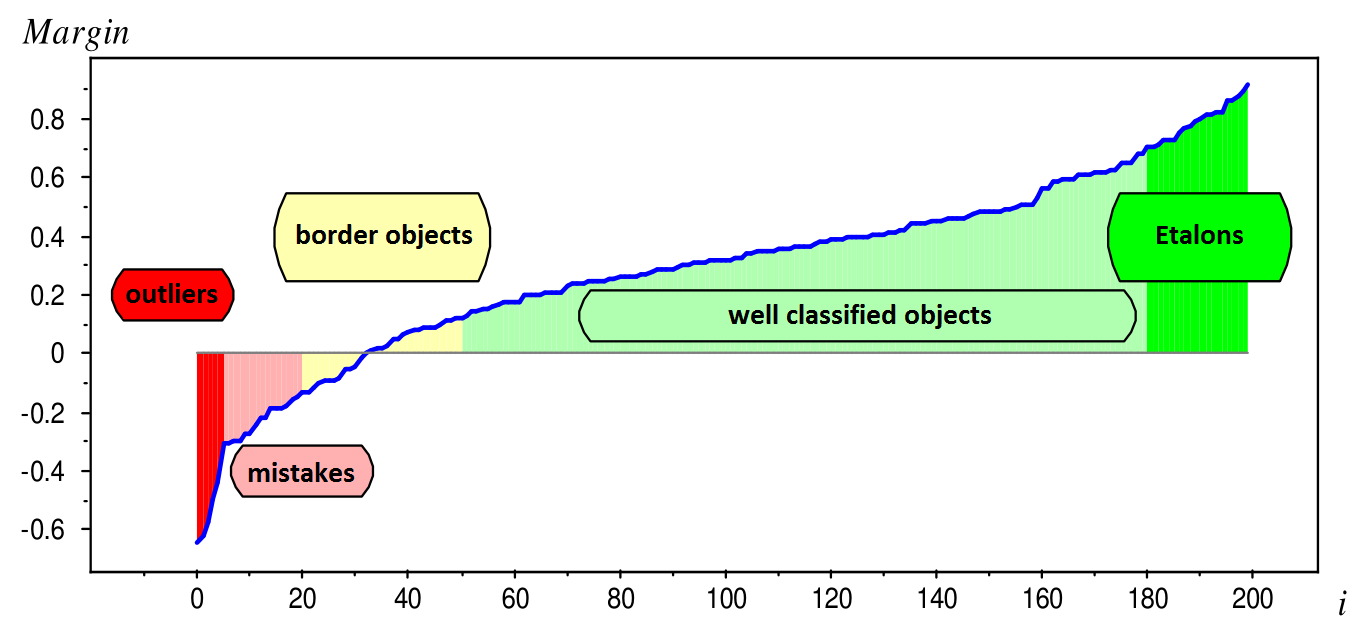
Отлично! Значит нам надо просто минимизировать ошибки классификации для всех объектов:

$$L(w) = \sum_i [y^{(i)} g(x^{(i)}) < 0] \rightarrow \min_w$$

Проблема в том, что это будет комбинаторная оптимизация. Существуют различные аппроксимации этой функции ошибок:

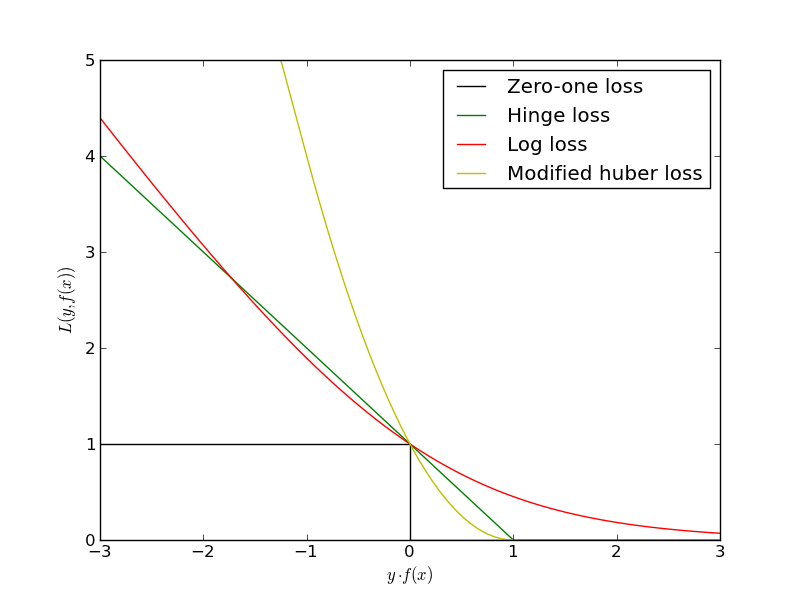
Другая постановка

Рассмотрим принадлежность к классу $y=\pm1$ некого объекта $x$: $$p(y=\pm1 | x,w)$$ и выразим её через сигмойду от отступа:

$$p(y=\pm1|x,w) = \sigma(y (\langle w, x \rangle + w_0)) = \sigma(y^{(i)} g(x^{(i)}))$$

А ошибка, которую мы будем минимизировать - логарифмическая:

$$L(w) = - \frac{1}{N}\sum_i \log(\sigma(y^{(i)} g(x^{(i)})) = \frac{1}{N}\sum_i \log(1 + e^{-y^{(i)} g(x^{(i)})}) \rightarrow \min_w$$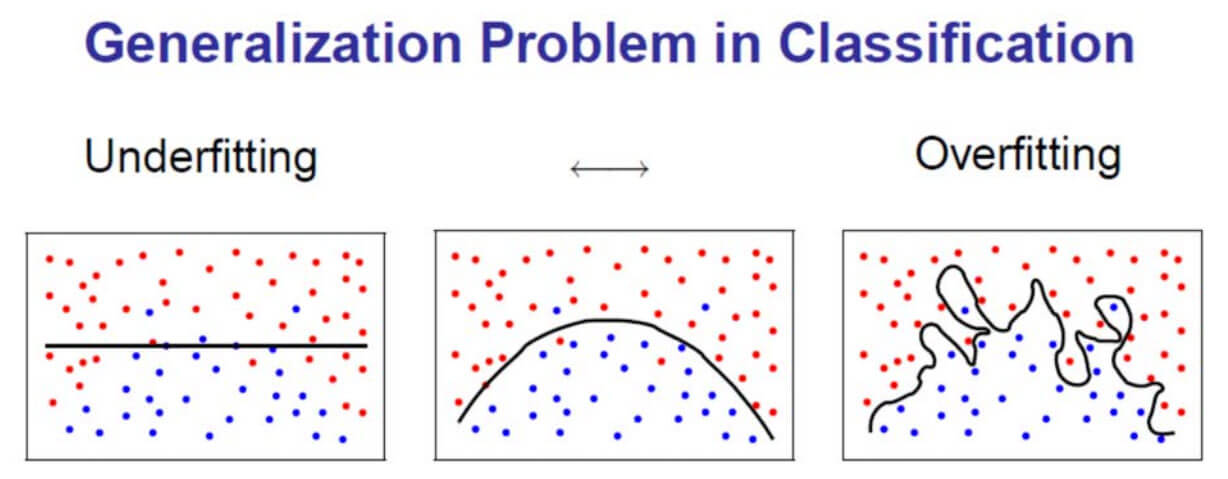
  • Как искать $w$? - c помощью градиентного спуска!
  • А что с регуляризацией? - та же история
    • Lasso: $ \frac{1}{C} \sum\limits_{j=1}^d |w_j|$
    • Rigde: $ \frac{1}{C} \sum\limits_{j=1}^d w_j^2$

Многоклассовая классификация

  • А если классов несколько?
    • 1-vs-1
    • 1-vs-rest
    • Softmax

Softmax

Для каждого класса определяется свой набор весов $$ \begin{cases} g_1(x)=w_{1}^{T}x + w_{0,1} \\ g_{2}(x)=w_{2}^{T}x + w_{0,2}\\ \cdots\\ g_{C}(x)=w_{C}^{T}x + + w_{0,C} \end{cases} $$

Нормировка "скоров" классов

$$ p(y=c|x)=softmax(g_c|W, x)=\frac{exp(w_{c}^{T}x + w_{0,c})}{\sum_{i}exp(w_{i}^{T}x + w_{0,i})} $$