Методы машинного обучения
Шестаков Андрей (avshestakov@hse.ru)
Линейные модели классификации. Методы понижения размерности
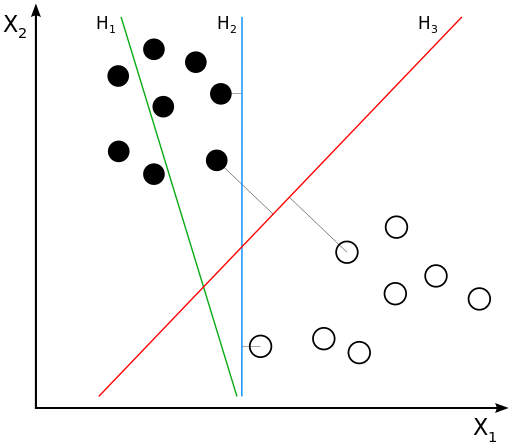
Нам надо найти уравнение прямой (гиперплоскости), которая бы могла разделить два класса ($H_2$ и $H_3$ подходят). В данном случае, уравнение прямой задаётся как: $$g(x) = w_0 + w_1x_1 + w_2x_2 = \langle w, x \rangle + w_0 = w^\top x + w_0$$
- Если $g(x^*) > 0$, то $y^* = \text{'черный'} = +1$
- Если $g(x^*) < 0$, то $y^* = \text{'белый'} = -1$
- Если $g(x^*) = 0$, то мы находимся на линии
Перед тем как мы начнем, рассмотрим функцию $$\sigma(z) = \frac{1}{1 + exp{(-z)}},$$она называется сигмойда.
def sigmoid(z):
return 1./(1+np.exp(-z))
demo_sigmoid()
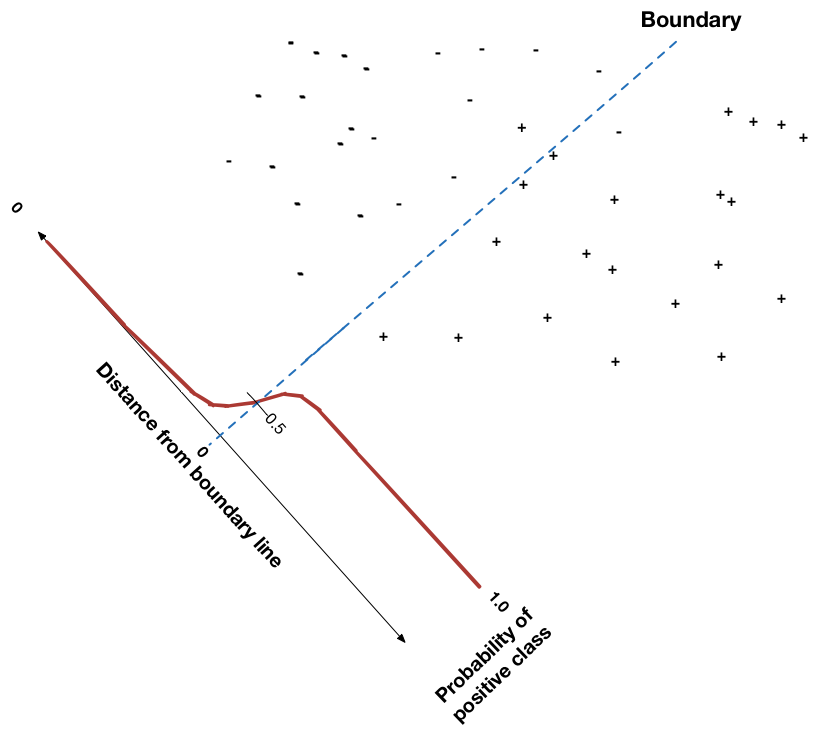
Постановка задачи¶
Будем требовать, чтобы алгоритм возвращал вероятность класса $y=+1$: $$h(x,w) = p(y=+1|x,w) = \sigma(g(x))$$
Выпишем функцию правдоподобия $$ \mathcal{L}(w) = \prod_i^n h(x^{(i)},w)^{[y^{(i)} = +1]} (1 - h(x^{(i)},w))^{[y^{(i)} = -1]} \rightarrow \max_w$$ $$ -\log{\mathcal{L}(w)} = - \sum_i^n [y^{(i)} = +1]\cdot\log{(h(x^{(i)},w))} + {[y^{(i)} = -1]}\cdot\log{(1-h(x^{(i)},w))} \rightarrow \min_w$$ $$L(w) = \log{\mathcal{L}(w)} \rightarrow \min_w $$
logloss_demo()
Рассмотрим объекты со следующими признаками:
| x1 | x2 |
|---|---|
| 0 | 1 |
| 1 | 0 |
| 1 | 1 |
| 2 | 2 |
| 2 | 3 |
| 3 | 2 |
Определите к какому классу относятся наблюдения, если вектор параметров имеет вид $(w_0 = -0.3 , w_1 = 0.1, w_2 = 0.1)$
X = np.array([[0,1],[1,0],[1,1],[2,2],[2,3],[3,2]])
w = np.array([.1, .1])
w0 = -.3
sigmoid(X.dot(w) + w0)
array([0.450166 , 0.450166 , 0.47502081, 0.52497919, 0.549834 ,
0.549834 ])
Другая постановка¶
Вспоминаем¶
$$g(x) = w_0 + w_1x_1 + w_2x_2 = \langle w, x \rangle + w_0 = w^\top x + w_0$$- Если $g(x^*) > 0$, то $y^* = \text{'черный'} = +1$
- Если $g(x^*) < 0$, то $y^* = \text{'белый'} = -1$
- Если $g(x^*) = 0$, то мы находимся на линии
- т.е. решающее правило: $y^* = sign(g(x^*))$
Величину $M_i = y^{(i)} \cdot g(x^{(i)})$ называют отступом(margin)
Если для какого-то объекта $M_i \geq 0$, то его классификация выполнена успешно.
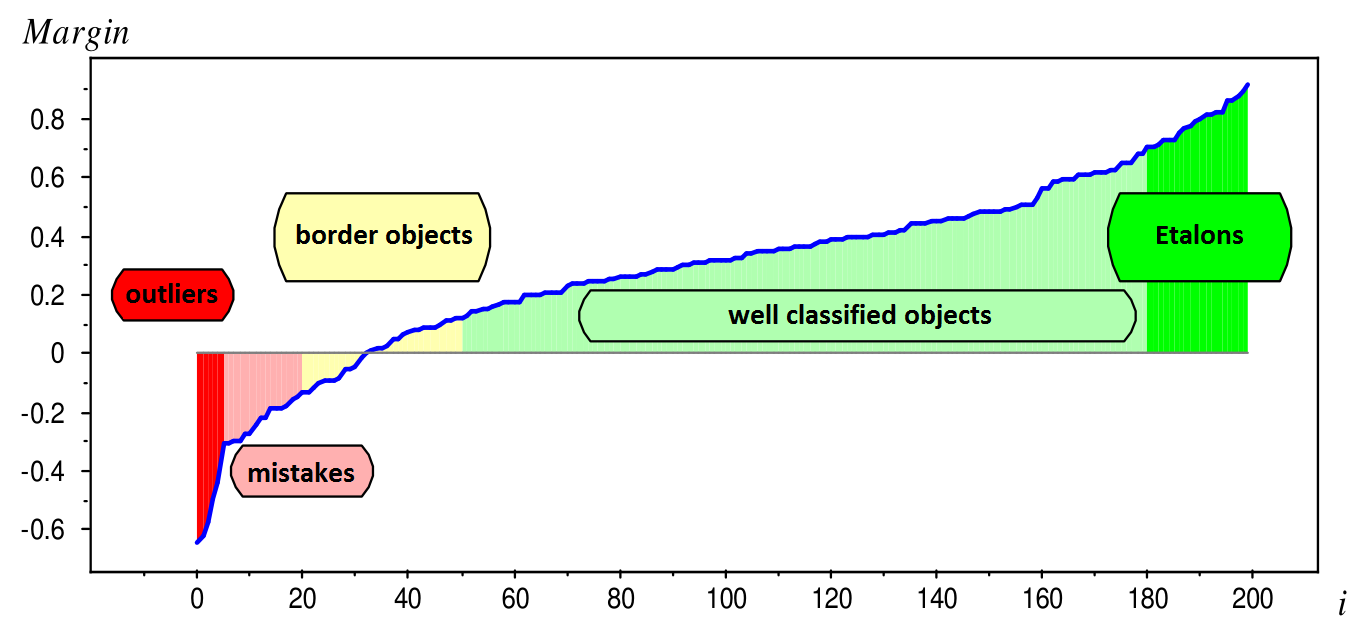
Отлично! Значит нам надо просто минимизировать ошибки классификации для всех объектов:
$$L(w) = \sum_i [y^{(i)} g(x^{(i)}) < 0] \rightarrow \min_w$$Проблема в том, что это будет комбинаторная оптимизация. Существуют различные аппроксимации этой функции ошибок:
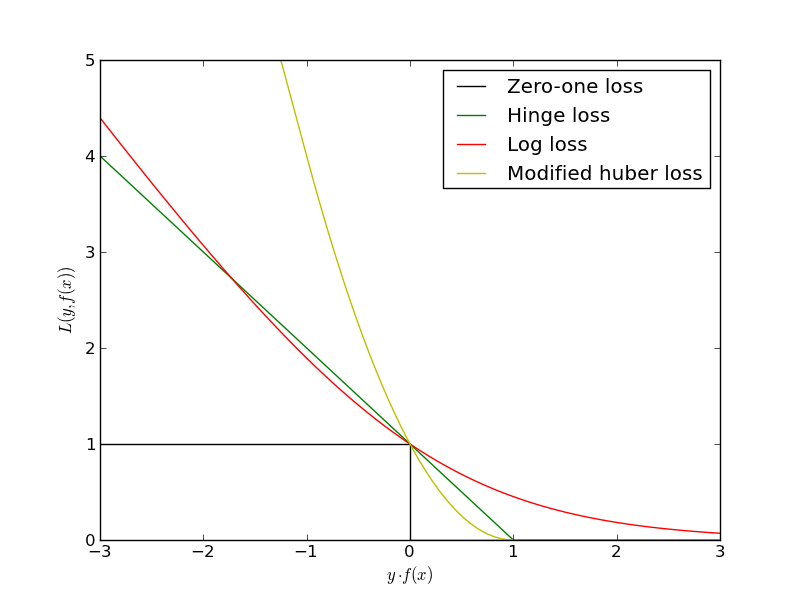
Другая постановка¶
Рассмотрим принадлежность к классу $y=\pm1$ некого объекта $x$: $$p(y=\pm1 | x,w)$$ и выразим её через сигмойду от отступа:
$$p(y=\pm1|x,w) = \sigma(y (\langle w, x \rangle + w_0)) = \sigma(y^{(i)} g(x^{(i)}))$$А ошибка, которую мы будем минимизировать - логарифмическая:
$$L(w) = - \frac{1}{N}\sum_i \log(\sigma(y^{(i)} g(x^{(i)})) = \frac{1}{N}\sum_i \log(1 + e^{-y^{(i)} g(x^{(i)})}) \rightarrow \min_w$$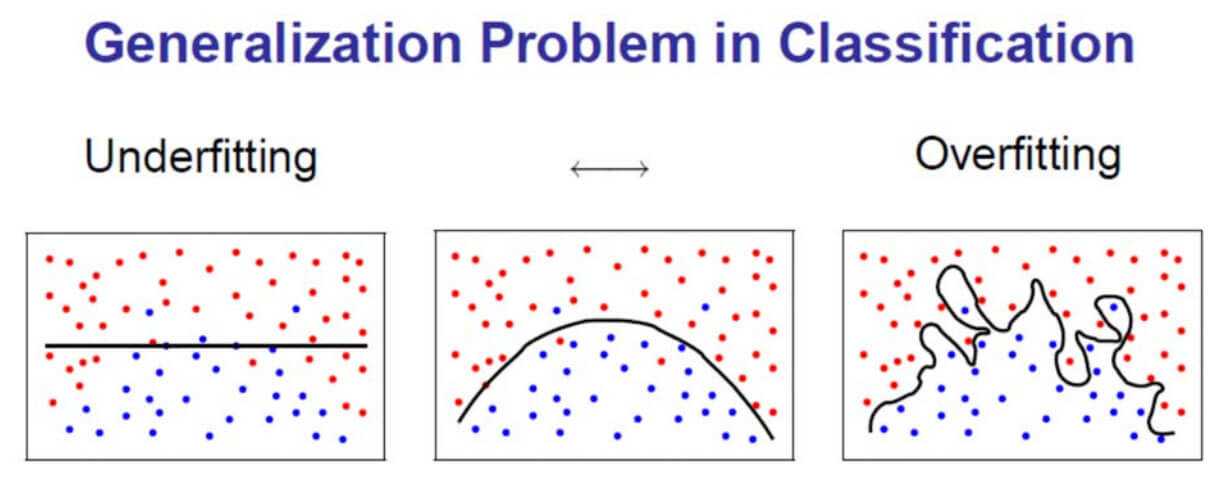
- Как искать $w$? - c помощью градиентного спуска!
- А что с регуляризацией? - та же история
- Lasso: $ \frac{1}{C} \sum\limits_{j=1}^d |w_j|$
- Rigde: $ \frac{1}{C} \sum\limits_{j=1}^d w_j^2$
Softmax¶
Для каждого класса определяется свой набор весов $$ \begin{cases} g_1(x)=w_{1}^{T}x + w_{0,1} \\ g_{2}(x)=w_{2}^{T}x + w_{0,2}\\ \cdots\\ g_{C}(x)=w_{C}^{T}x + + w_{0,C} \end{cases} $$
Нормировка "скоров" классов
$$ p(y=c|x)=softmax(g_c|W, x)=\frac{exp(w_{c}^{T}x + w_{0,c})}{\sum_{i}exp(w_{i}^{T}x + w_{0,i})} $$Методы понижения размерности признаков¶

Проклятье размености¶
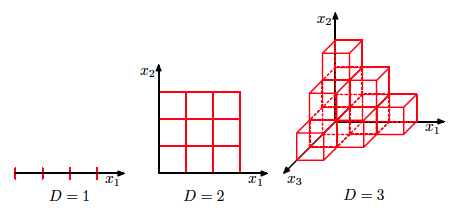
Проклятье размерности¶
$d=2$ |
$d=2 \dots 100$ |
|---|
Для чего можно понижать размерность признаков?¶
- Cмотреть на 2-3 признака удобнее чем на 100
- Потенциально может улучшить качество моделей
- Удаление лишних коррелирующих признаков
- Ускоряет обучение
- Данные занимают меньше места
- Меньше признаков - легче интерпретировать модели
Способы понижения размерности¶
Избавляться от размерности можно методами отбора признаков (Feature Selection) и методами уменьшения размерности (Feature Reduction)
Глобальная разница
- Feature Selection: не используем часть признаков
- Feature Reduction: исходные признаки проходят через некоторое преобразование $f(\cdot)$, и на выходе признаков становится меньше
Feature Selection¶
Методы деляться на следующие группы:
- Unsupervised methods
- Определяем полезность признака вне зависимости от целевой переменной
- Filter methods
- Признаки рассматриваются независимо друг от друга
- Изучается индивидуальный "вклад" призника в предсказываемую переменную
- Быстрое вычисление
- Пример?
- Wrapper methods
- Идет отбор группы признаков
- Может быть оооочень медленным, но качество, обычно, лучше чем у Filter Methods
- Примеры: Stepwise feature selection for regression, Boruta Algorithm
- Embedded methods
- Отбор признаков "зашит" в модель
Filter method - Mutual Information¶
$$MI(y,x) = \sum_{x,y} p(x,y) \ln\left[\frac{p(x,y)}{p(x)p(y)}\right]$$Сколько информации $x$ сообщает об $y$.
df_titanic = pd.read_csv('titanic.csv')
df_titanic.head()
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
from sklearn.metrics import mutual_info_score
pd.crosstab(df_titanic.Survived, df_titanic.Sex, normalize=True)
mutual_info_score(df_titanic.Survived.values,
df_titanic.Sex.values)
0.15087048925218183
Wrapper Methods - Recursive Feature Elimination¶
При данном подходе из линейной модели последовательно удаляются признаки с наименьшим коэффициентом
Интерпретация¶
- Интерпретация 1: находит такие ортогональные оси, вдоль которых дисперсия данных максимальна
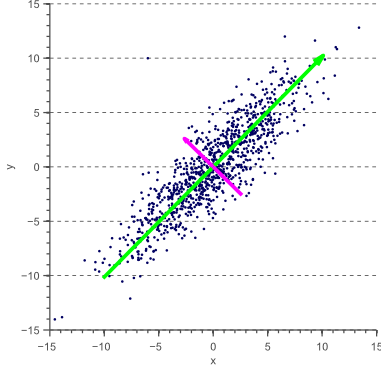
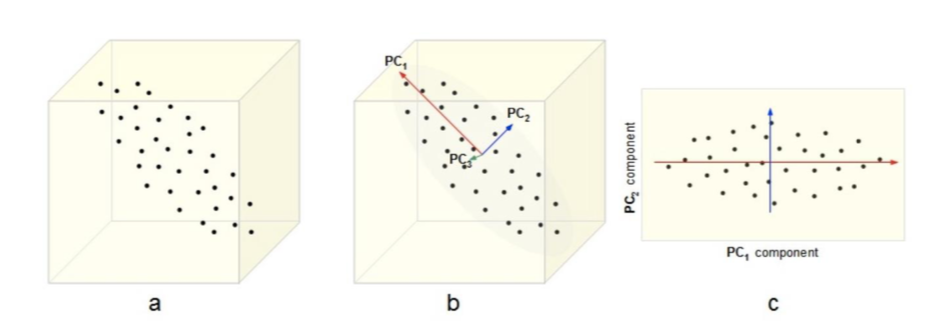
Интерпретация¶
- Интерпретация 2: Найти такое подпространство меньшей размерности $L$ Такое что различие между точками и их проекциями минимальна
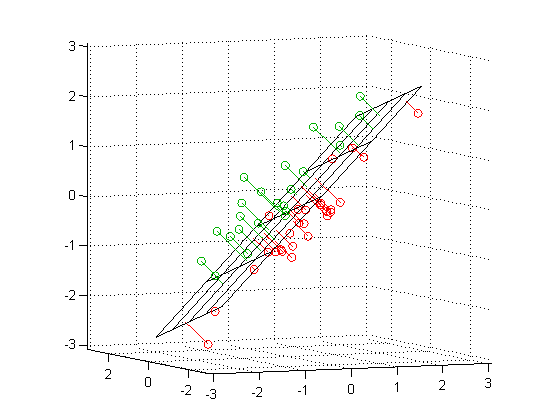
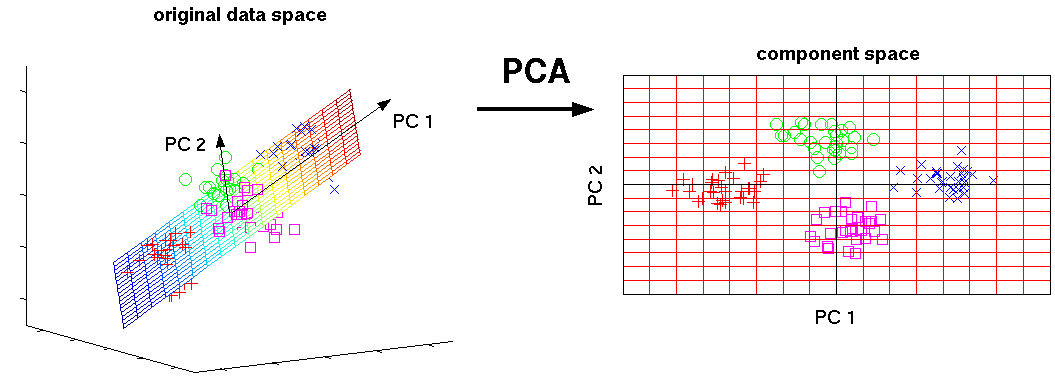
В двух словах:¶
- Совершаем переход к новым осям, так что:
- Новые переменные являются линейной комбинацией старых переменных
- Новые оси ортогональны друг другу
- Дисперсия вдоль новых осей максимальная
Что значит "перейти к новым координатам"?¶
- Пусть у нас есть объект $x$ с тремя признаками: $x=(-0.343, -0.754, 0.241)$
- Можно сказать, что он представлен в пространстве, натянутом на 3 стандартных базистых вектора: $$ e_1 = \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right) \quad e_2 = \left( \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right) \quad e_3 = \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) \quad$$
- Предположими мы хотим перейти к другому базису, например:
- Как спроицировать наш объект $x$ из исходного базиса в данный?
Проецируем¶
$$ w_1 = \left( \begin{array}{c} -0.390 \\ 0.089 \\ -0.916 \end{array} \right) \quad w_2 = \left( \begin{array}{c} -0.639 \\ -0.742 \\ 0.200 \end{array} \right) \quad w_3 = \left( \begin{array}{c} -0.663 \\ 0.664 \\ 0.346 \end{array} \right) \quad$$$$ z = W^\top x = \left( \begin{array}{ccc} -0.390 & 0.089 & -0.916\\ -0.639 & -0.742 & 0.200 \\ -0.663 & 0.664 & 0.346 \end{array} \right) \left( \begin{array}{c} -0.343 \\ -0.754 \\ 0.241 \end{array} \right) = \left( \begin{array}{c} -1.154 \\ 0.828 \\ 0.190 \end{array} \right)$$То есть: $$ x = -1.154 w_1 + 0.828 w_2 + 0.190 w_3$$
(Пример взят из Mohammed J. Zaki, Ch7 )
- Проецировать научились, осталось только понять как же находить эти самые $w$?
- Новые оси ортогональны друг другу
- Дисперсия вдоль новых осей максимальна
Находим главные компоненты¶
Новые оси ортогональны друг другу: $$\langle w_{i},w_{j}\rangle=\begin{cases} 1, & i=j\\ 0 & i\ne j \end{cases}$$
Дисперсия вдоль новых осей максимальна
- Предполагаем, что исходные признаки центрированы (и шкалированы) $$ \begin{align} \sigma^2_w & = \frac{1}{n}\sum\limits_{i=1}^n(z_i - \mu_z)^2 \\ & = \frac{1}{n}\sum\limits_{i=1}^n(w^\top x_i)^2 \\ & = \frac{1}{n}\sum\limits_{i=1}^n w^\top( x_i x_i^\top) w \\ & = w^\top \left(\frac{1}{n}\sum\limits_{i=1}^n x_i x_i^\top \right) w \\ & = w^\top C w \rightarrow \max_w \\ \end{align} $$
$C = X^\top X$ - ковариационная матрица
Находим главные компоненты¶
То есть, чтобы найти первую главную компоненту, надо решить такую задачу: $$ \begin{equation} \begin{cases} w_1^\top X^\top X w_1 \rightarrow \max_{w_1} \\ w_1^\top w_1 = 1 \end{cases} \end{equation} $$
Решение для первой компоненты¶
Изначально было так $$ w_1^\top X^\top X w_1 \rightarrow \max_{w_1}$$
- Строим лагранжиан $$ \mathcal{L}(w_1, \nu) = w_1^\top X^\top X w_1 - \nu (w_1^\top w_1 - 1) \rightarrow max_{w_1, \nu}$$
- Считем производную по $w_1$ $$ \frac{\partial\mathcal{L}}{\partial w_1} = X^\top X w_1 - \nu w_1 = 0 \Leftrightarrow X^\top X w_1 = \nu w_1$$
Подставим одно в другое: $$ w_1^\top X^\top X w_1 = \nu w_1^\top w_1 = \nu \rightarrow \max$$
Задача о собственном векторе, собственном числе матрицы¶
Пусть для матрицы $A$ существует ненулевой вектор $v$ и число $\lambda$ такие, что $$Av=\lambda v$$ Тогда вектор $v$ называют собственным вектором оператора $A$, а число $\lambda$ - соответствующим собственным числом оператора $A$.
Оказывается, что у матрицы ковариций $X^\top X$:
- Все собственные числа $\lambda_i \in \mathbb{R}, \lambda_i \geq 0$ (упорядочим индексы по возрастанию так, что $\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_d $)
- Собственные вектора при $\lambda_i \neq \lambda_j $ ортогональны: $v_i^\top v_j = 0$
- Для уникальных $\lambda_i$ уникальны и $v_i$
Решение для первой компоненты¶
Изначально было так $$ w_1^\top X^\top X w_1 \rightarrow \max_{w_1}$$
- Строим лагранжиан $$ \mathcal{L}(w_1, \nu) = w_1^\top X^\top X w_1 - \nu (w_1^\top w_1 - 1) \rightarrow max_{w_1, \nu}$$
- Считем производную по $w_1$ $$ \frac{\partial\mathcal{L}}{\partial w_1} = X^\top X w_1 - \nu w_1 = 0 \Leftrightarrow X^\top X w_1 = \nu w_1$$
Подставим одно в другое: $$ w_1^\top X^\top X w_1 = \nu w_1^\top w_1 = \nu \rightarrow \max$$
Что значит, что:
- $\nu$ - наибольшее собственное число матрицы $X^\top X$, а именно - $\lambda_1$
- $w_1$ - собственный вектор при $\lambda_1$
Задача и решение для второй компоненты¶
$$ \begin{equation} \begin{cases} w_2^\top X^\top X w_2 \rightarrow \max_{w_2} \\ w_2^\top w_2 = 1 \\ w_2^\top w_1 = 0 \end{cases} \end{equation} $$Аналогичными операциями мы прийдем к тому, что $w_2$ - собственный вектор при втором по величине собственном числе матрицы $X^\top X$.
То есть поиск главных компонент сводится к поиску собственных векторов и собственных чисел матрицы $X^\top X$!
Алгоритм¶
- Центрируем и шкалируем исходные признаки
- Считаем матрицу ковариаций $X^\top X$
- Находим $k$ главных компонент и собственных чисел $$W = \left[ \begin{array}{cccc} \mid & \mid & & \mid\\ w_{1} & w_{2} & \ldots & w_{k} \\ \mid & \mid & & \mid \end{array} \right] $$
- Проецируем на них: $$ Z = XW $$
Сколько компонент брать или зачем нужны $\lambda$?¶
- Из предыдущих слайдов мы помним, что $$w_1^\top X^\top X w_1 = \lambda_1$$ То есть $\lambda_1$ равна дисперсии точек, спроецированных на первую базовую компоненту
- Величина $$ \frac{\lambda_{i}}{\sum_{d=1}^{D}\lambda_{d}} $$ Показывает долю объясненной дисперии компоненты $i$
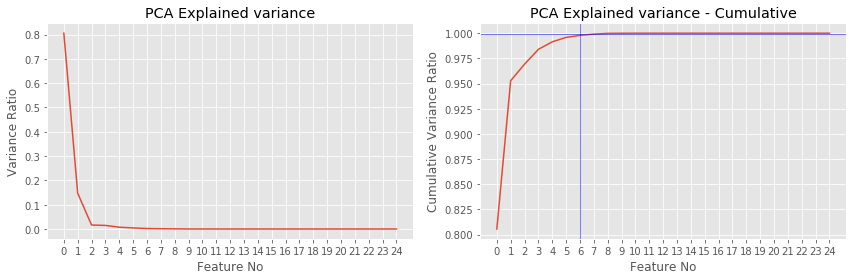
MNIST, DIGITS¶

MNIST PCA¶

Резюме¶
- PCA понижает размерность признакового пространства
- Новые компоненты являются линейной комбинацией исходных признаков
- Новые компоненты (не признаки) - ортогональны
- Можно применять в моделях и для визуализации
- Tutorial 1
- PCA SVD туториал
Многомерное шкалирование¶
Идея¶
- Перейти в пространство меньшей размерности так, чтобы расстояния между объектами в новом пространстве были подобны расстояниям в исходном пространстве.
- Дано $X = [x_1,\dots, x_n]\in \mathbb{R}^{N \times D}$ и/или $\delta_{ij}$ - мера близости между $(x_i,x_j)$
- Надо найти $Y = [y_1,\dots,y_n] \in \mathbb{R}^{N \times d}$ такие, что $\delta_{ij} \approx d(y_i, y_j) = \|y_i-y_j\|^2$
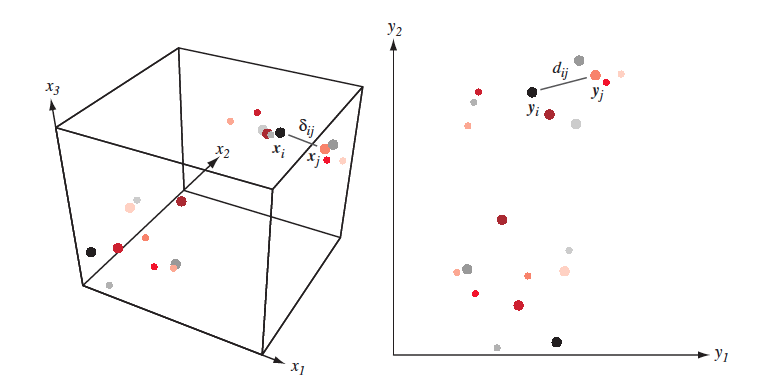
Понятно, что точно воспроизвести расстояния получится не всегда
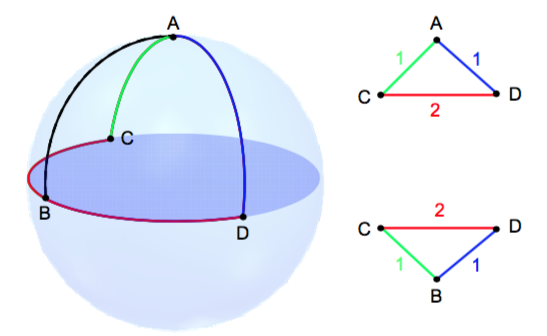
Подходы¶
- Классический (cMDS)
- Метрический (metric MDS)
- Неметрический (non-metric MDS)
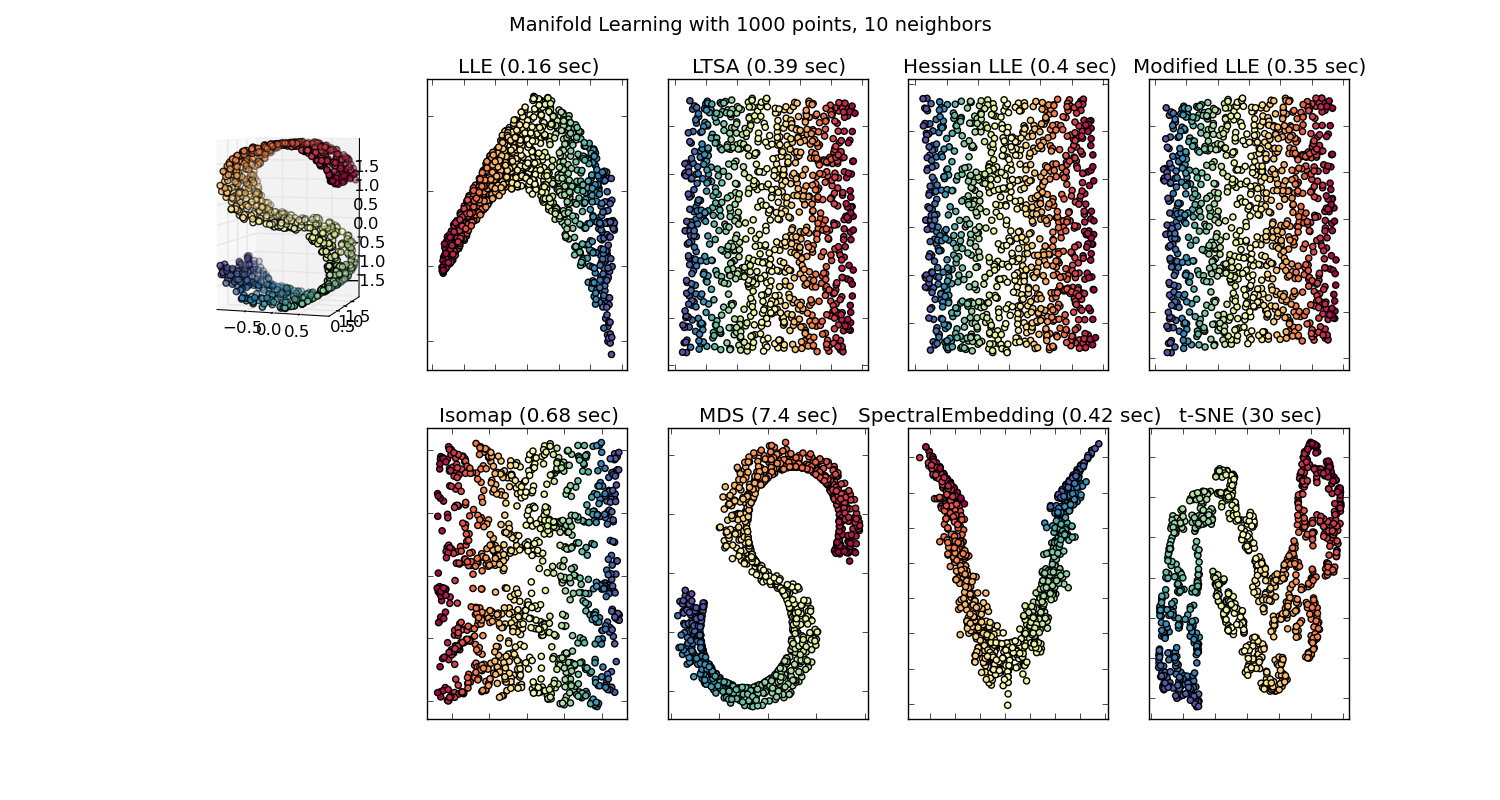
- t-SNE - практически многомерное шкалирование
- Вместо этого мы будем пытаться перенести "окрестность" точек из исходного пространства в пространоство меньшей размерности
- Полученные расстояния скорее всего не будут соотносится с исходными
- Схожесть между объектами в исходном пространстве $\mathbb{R}^m$ $$ p(i, j) = \frac{p(i | j) + p(j | i)}{2n}, \quad p(j | i) = \frac{\exp(-\|\mathbf{x}_j-\mathbf{x}_i\|^2/{2 \sigma_i^2})}{\sum_{k \neq i}\exp(-\|\mathbf{x}_k-\mathbf{x}_i\|^2/{2 \sigma_i^2})} $$ $\sigma_i$ неявно задается пользователем
- Схожесть между объектами в целевом пространстве $\mathbb{R}^k, k << m$ $$ q(i, j) = \frac{g(|\mathbf{y}_i - \mathbf{y}_j|)}{\sum_{k \neq l} g(|\mathbf{y}_i - \mathbf{y}_j|)} $$ где $g(z) = \frac{1}{1 + z^2}$ - распределение Коши (t-распределение Стьюдента с 1 степенью свободы)
- Критерий $$ J_{t-SNE}(y) = KL(P \| Q) = \sum_i \sum_j p(i, j) \log \frac{p(i, j)}{q(i, j)} \rightarrow \min\limits_{\mathbf{y}} $$
Дивергенция Кульбака-Лейблера¶
- Насколько распределение $P$ отличается от распределения $Q$? $$ KL(P \| Q) = \sum_z P(z) \log \frac{P(z)}{Q(z)} $$
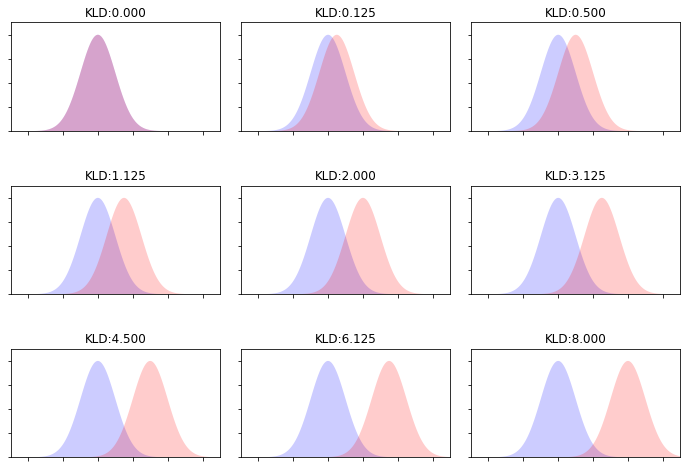
Оптимизация¶
- Оптимизируем $J_{t-SNE}(y)$ с помощью градиентного спуска
- Статья
- Примеры
- Демо и советы
- t-SNE может быть нестабильным
- Размеры полученных сгустков могут ничего не значить
- Расстояния между кластерами могут ничего не значить
- Полностью шумовые данные могут выдать структуру