Методы машинного обучения

 Шестаков Андрей (avshestakov@hse.ru)

---

Методы кластеризации

%matplotlib inline

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy

plt.style.use('seaborn-talk')
plt.rcParams['figure.figsize'] = (12,8)

import warnings
warnings.filterwarnings('ignore')

# Для кириллицы на графиках
font = {'family': 'Verdana',
        'weight': 'normal'}
plt.rc('font', **font)

try:
    from ipywidgets import interact, IntSlider, fixed, FloatSlider
except ImportError:
    print(u'Так надо')
    
from IPython.display import YouTubeVideo

Цели и задача кластеризации

Задача

Основная задача кластерного анализа — разбиение исходного набора объектов на группы (кластеры) таким образом, чтобы:

1. Объекты в группе были похожи друг на друга,
2. Объекты из разных групп - отличались

Цели

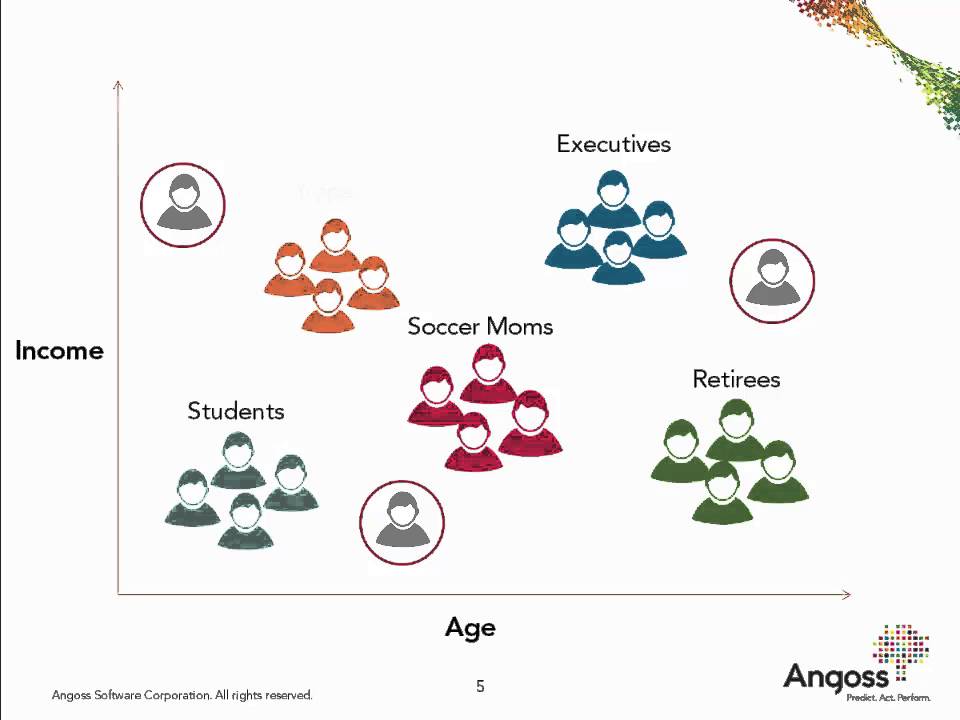
• Поиск структуры в данных и ее интерпретация
• Поиск аномальных объектов
• Детальный анализ отдельных кластеров

Кластеризация

Выявление сообществ в сети*

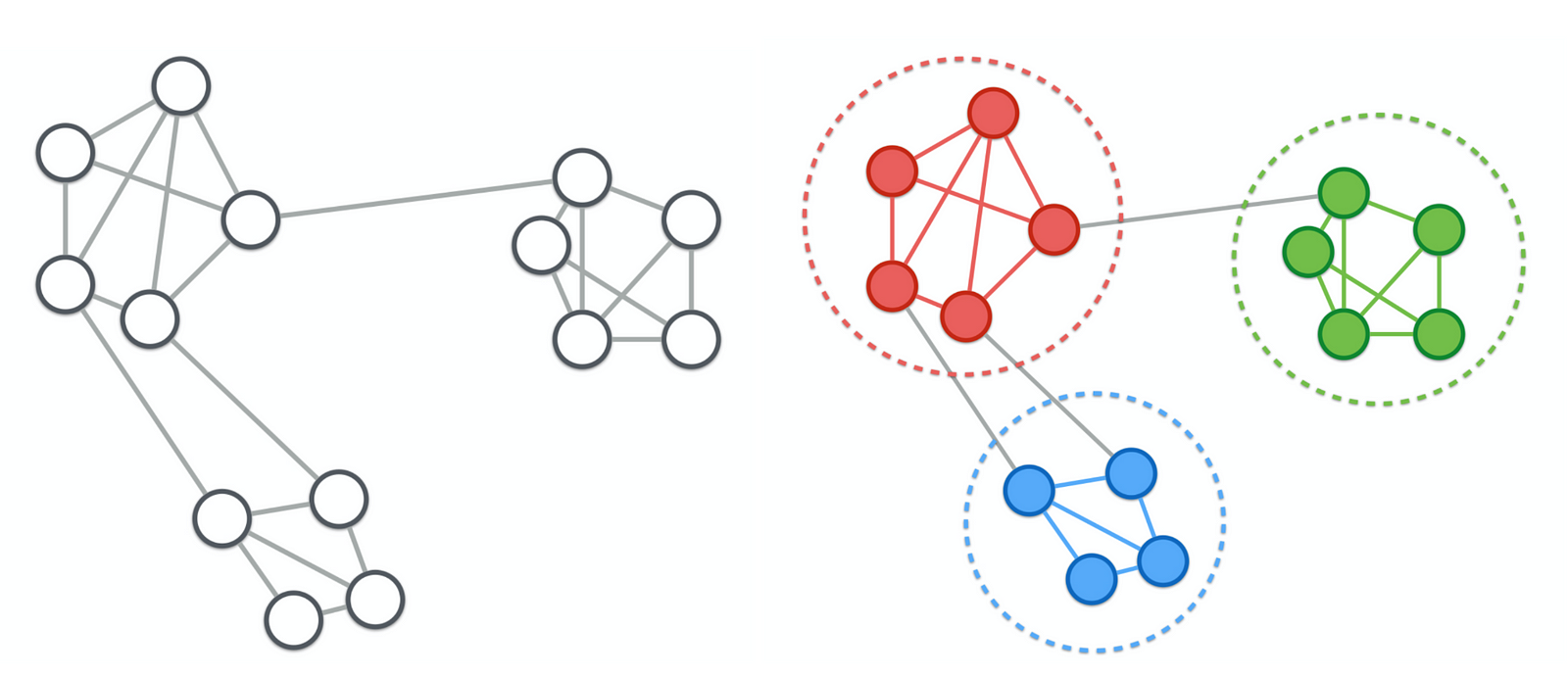
Группы методов

• Методы основанные на прототипах
  • Каждый кластер ассоциируется с виртуальрным "эталонным" объектом
• Иерархические методы
  • Не простое разбиение на целая иерархия
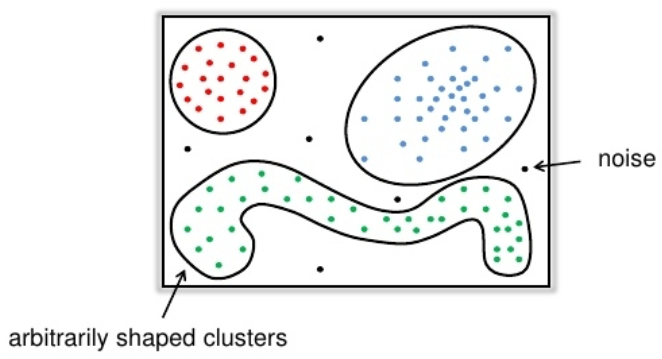
• Плотностные методы
  • Ищем плотные скопления точек в признаковом пространстве
• Вероятностные методы
  • Предполагаем, что данные порождены некоторой смесью вероятностных распределений
• Спектральные методы
• Сеточные методы

Отличительные особенности методов

• Вычислительная сложность
• Результат в виде
  • разбиения (hard clustering, partition),
  • распределения (soft clustering) или
  • иерархии (hierarchy)
• Форма и размер кластеров на выходе
• Устойчивость к выбросам

Метод k-средних

Алгоритм k-means

• Дано множество объектов $X = \{x_1, x_2, \dots, x_N\}$
• Кластер $C_k \Leftrightarrow \text{ центройд } \mu_k$
• Объект $x_i \in C_k \Leftrightarrow \mu_k = \arg \min\limits_{\mu_j} \|x_i - \mu_j \|^2$
• Надо найти такое разбиение на $K$ кластеров, чтобы минизировать $$ L(C) = \sum_{k=1}^K\sum_{i\in C_k} ||x_i - \mu_k||^2 \rightarrow \min\limits_C $$ $$\mu_k = \frac{1}{|C_k|} \sum _{x_n \in C_k} x_n$$

Алгоритм k-means

1. Выбрать $K$ начальных центроидов случайным образом $\rightarrow \mu_k, \ k=1\dots K$
2. Для каждой точки из датасета присвоить кластер, соответствующий ближайшему центроиду $$C_k = \{x_n : ||x_n - \mu_k||^2 \leq ||x_n - \mu_l||^2 \quad \forall l \neq k \} $$
3. Обновить центройды: $$\mu_k = \frac{1}{|C_k|} \sum _{x_n \in C_k} x_n$$
4. Повторять 2 и 3 до тех пор, пока изменения перестанут быть существенными

Основные факторы

• Начальная инициализация центройдов
• Количество кластеров

Kак выбрать K?

• Не пользоваться обычным k-means (X-means, ik-means)
• Посмотреть на меры качества кластеризации (об этом потом)
• Воспользоваться эвристиками

Elbow method (Метод локтя)

• Критерий минимизации k-means $$ L(C) = \sum_{k=1}^K\sum_{i\in C_k} ||x_i - \mu_k||^2 \rightarrow \min\limits_C $$
• Давайте возьмем всевозможные $K$, для каждого запустим алгоритм, посчитаем на результате $L(C)$ и выберем минимум!

• Ничего не выйдет... Почему?

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans

X, y = make_blobs(n_samples=500,
                  n_features=2,
                  centers=4,
                  cluster_std=1,
                  center_box=(-10.0, 10.0),
                  shuffle=True,
                  random_state=1) 


crit = []

for k in range(2, 8):
    kmeans = KMeans(n_clusters=k, random_state=1).fit(X)
    crit.append(np.sqrt(kmeans.inertia_))
    
def elbow_demo(k=2):
    
    X, y = make_blobs(n_samples=500,
                  n_features=2,
                  centers=4,
                  cluster_std=1,
                  center_box=(-10.0, 10.0),
                  shuffle=True,
                  random_state=1) 
    
    kmeans = KMeans(n_clusters=k, random_state=1).fit(X)
    
    fig, ax = plt.subplots(1,2)
    
    ax[0].scatter(X[:,0], X[:,1], c=kmeans.labels_)
    
    ax[0].scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
                  marker='o', c="white", alpha=1, s=200)
    
    ax[0].set_xlabel('$x_1$')
    ax[0].set_ylabel('$x_2$')

    for i, c in enumerate(kmeans.cluster_centers_):
        ax[0].scatter(c[0], c[1], marker='$%d$' % i, alpha=1, s=50)
        
    ax[1].plot(range(2,8), crit, marker='s')
    
    ax[1].set_xlabel('$k$')
    ax[1].set_ylabel('$L^{(k)}(C)$')
    
    plt.show()
    
    
    

Elbow method (Метод локтя)

• Выбирают такое $k$, после которого функционал $L(C)$ уменьшается не слишком быстро
• Чуть более формально: $$ D(k) = \frac{|L^{(k)}(C) - L^{(k+1)}(C)|}{|L^{(k-1)}(C) - L^{(k)}(C)|} \quad \text{"невелико"} $$

interact(elbow_demo, k=IntSlider(min=2,max=8,step=1,value=2))

<function __main__.elbow_demo(k=2)>

Важно!

• Эвристика и меры качества клатеризации носят лишь рекомендательный характер!
• Если они ничего не дают, то лучше ориентироваться на свои знания в предметной области
• Или "выжать" из полученной кластеризации максимум
  • 3 из 5 полученных кластеров интерпретируются - и то хорошо

Начальная инициализация центройдов

• Выбрать координаты $K$ случайных объектов из датасета
  • Производить случайные запуски много раз и выбрать наиболее оптимальную инициализацию
• Использовать результат другой кластеризации на $K$ кластеров
• k-means++

K-means++

• Первый центройд выбираем случайным образом из объектов датасета
• Для каждой точки рассчитываем расстояние $d_{\min}(x_i) = \min_{\mu_j} \|x_i - \mu_j\|^2$
• Точка назначается следующим центройдом с вероятностью $p(x_i) \propto d_{\min}(x_i)$

from sklearn.metrics import pairwise_distances

def demo_kmpp(iters=1):

    X, y = make_blobs(n_samples=550, cluster_std=1.5, n_features=2, centers=5, random_state=12345)

    X_grid1, X_grid2 = np.meshgrid(np.linspace(-12, 18, 500),
                                   np.linspace(-11, 8, 500))

    XX = np.c_[X_grid1.flatten(), X_grid2.flatten()]
    np.random.seed(1)
    centroids = np.empty((0, 2))

    for i in range(iters):
        if i == 0:
            d = np.ones_like(y, dtype=float)
        else:
            d = pairwise_distances(X, centroids, metric='euclidean').min(axis=1)
        weights = d/d.sum()

        centroid_idx = np.random.choice(X.shape[0], size=1, replace=False, p=weights)[0]
        centroids = np.r_[centroids, X[centroid_idx, np.newaxis]]

    d_grid = pairwise_distances(XX, centroids, metric='euclidean').min(axis=1)

    d_grid = d_grid.reshape(X_grid1.shape)
    d_grid = d_grid/d_grid.max()

    levels = np.linspace(0, 1, 100)

    plt.contourf(X_grid1, X_grid2, d_grid, cmap=plt.cm.Blues, alpha=0.7, levels=levels)
    plt.scatter(X[:, 0], X[:, 1], s=100)

    centers = centroids
    
    plt.scatter(centers[:, 0], centers[:, 1], marker='o',
                c="white", alpha=1, s=500, edgecolor='k')

    for i, c in enumerate(centers):
        plt.scatter(c[0], c[1], marker='$%d$' % (i+1), alpha=1,
                    s=100, edgecolor='k')

    plt.xlabel('$x_1$', fontsize=15)
    plt.ylabel('$x_2$', fontsize=15)

    plt.tight_layout()
    plt.axis('equal')
    plt.show()

interact(demo_kmpp, iters=IntSlider(min=1,max=6,step=1,value=1))

<function __main__.demo_kmpp(iters=1)>

Резюме

• Метод k-средних – жадный итеративный алгоритм
• Зависит от начальных центройдов и их количества

Преимущества

• Прост как пробка
• Имеет множество модификаций
  • Разные меры близости ($k$-medians, $k$-medoids)
  • Взвешивание признаков (Weighted $k$-means)
  • Нечеткая принадлежность кластеров (fuzzy $c$-means)
  • Для больших данных (batch $k$-means)
  • ...
• Интерпретация кластеров через центройды

Недостатки

• Подразумевает выпуклые кластеры

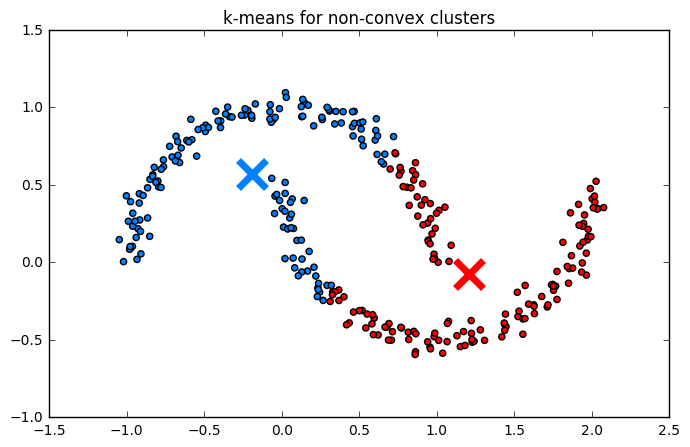
• Всегда* на выходе будет k кластеров

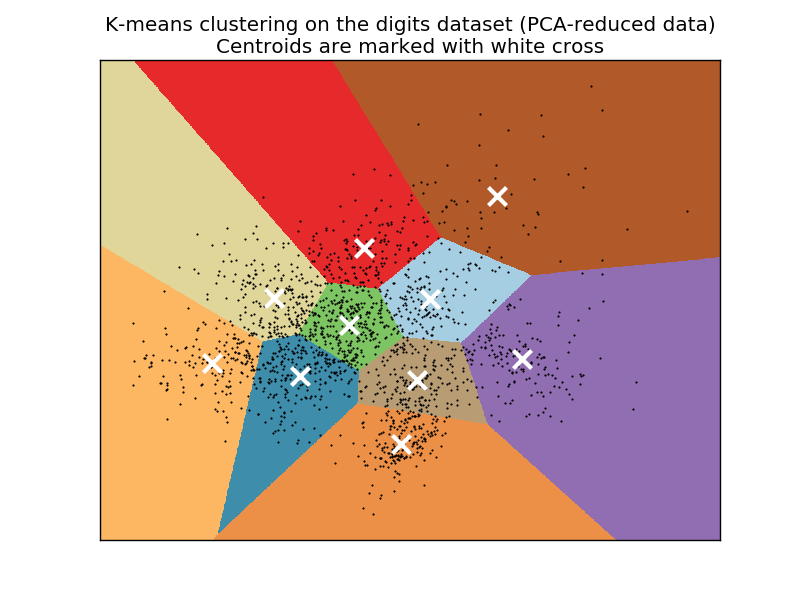
Иерархическая кластеризация

Мотивация

• Мы не всегда знаем сколько кластеров есть в данных
• Структура данных не всегда "плоская" - в ней может быть заложена иерархия!

Пример: семейства языков

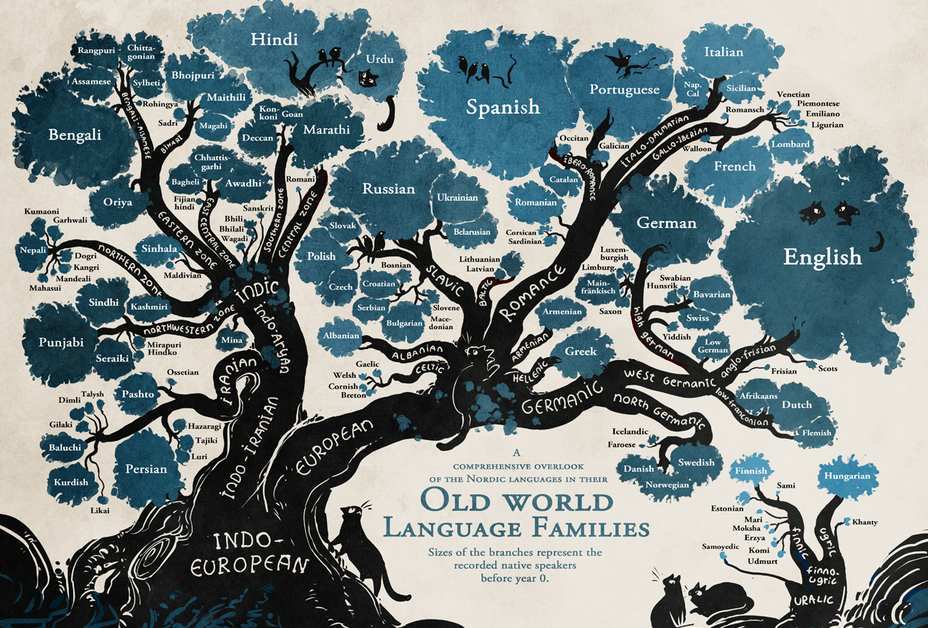
Аггломеративные алгоритмы

• начинаем с ситуации, когда каждый объект - отдельный кластер
• на каждом шаге совмещаем два наиболее близких кластера
• останавливаемся, когда получаем требуемое количество или единственный кластер

Дивизивные алгоритмы

• начинаем с ситуации, когда все объекты составляют один кластер
• на каждом шаге разделяем один из кластеров пополам
• останавливаемся, когда получаем требуемое количество или $N$ кластеров

Пример

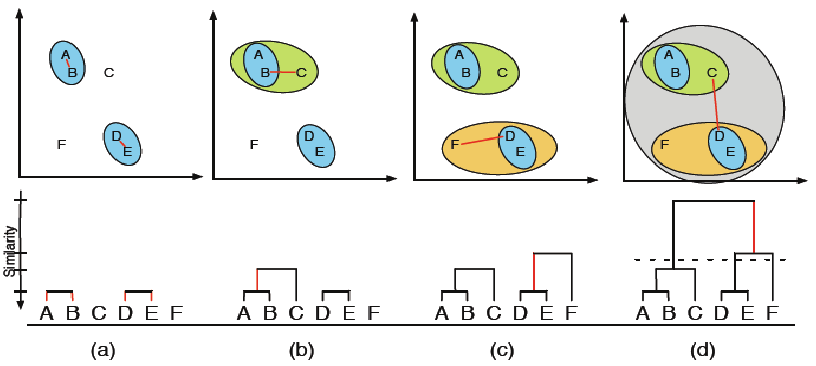
Дендрограмма

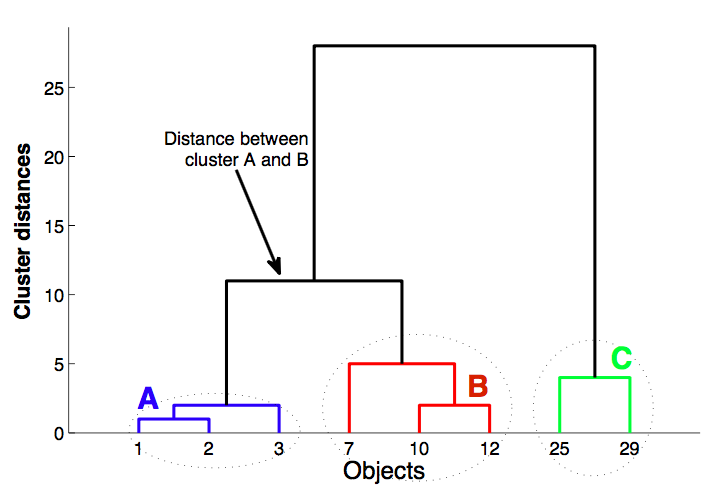
• Как определять близкие объекты?
• Как пересчитывать расстояние между кластерами после объединения?

Как определять близкие объекты? - Меры близости

см. лекцию про метрические методы

Пересчет расстояний после объединения кластеров

• Single linkage $$ d_{min}(C_i, C_j) = \min_{\mathbf{x} \in C_i, \mathbf{x}' \in C_j} \|\mathbf{x} -\mathbf{x}' \| $$

• Complete linkage $$ d_{max}(C_i, C_j) = \max_{\mathbf{x} \in C_i, \mathbf{x}' \in C_j} \|\mathbf{x} -\mathbf{x}' \| $$

• Average linkage $$ d_{avg}(C_i, C_j) = \frac{1}{n_i n_j}\sum_{\mathbf{x} \in C_i}\sum_{\mathbf{x}' \in C_j} \|\mathbf{x} -\mathbf{x}' \| $$

• Centroid linkage $$ d_{cent}(C_i, C_j) = \|\mu_i -\mu_j \| $$

• Ward linkage $$ d_{ward}(C_i, C_j) = \sqrt{\frac{n_i n_j}{n_i + n_j}} \|\mu_i - \mu_j \|$$

X = np.array([
        [1,1],
        [2,2],
        [2, 2.5],
        [5, 2],
        [4.5, 5],
        [3, 6],
        [5, 6],
        [6, 6]
    ])

plt.scatter(X[:,0], X[:,1])

<matplotlib.collections.PathCollection at 0x1a19685cc0>

# А теперь сделаем это с питоном
from scipy.cluster.hierarchy import dendrogram, linkage 
from scipy.cluster.hierarchy import fcluster, cophenet

Z = linkage(X, method='single', metric='euclidean')
dend = dendrogram(Z) 

Эвристика для оценки качества дендрограммы

• Кофенетическое расстояние между объектами $x_i$ и $x_j$ - высота дерева, при котором эти объекты объединились.

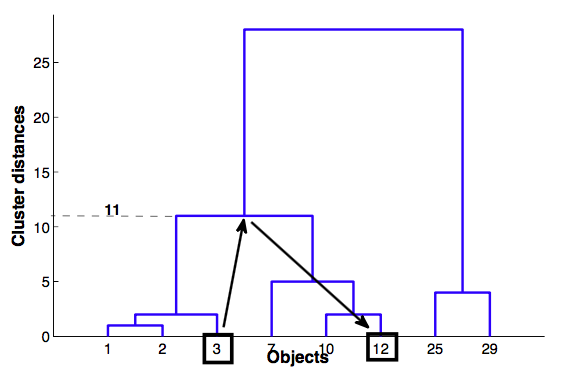
Кофенетическая корреляция

• Кофенетическая корреляция — коэффициент корреляции между массивами попарных расстояний и попарных кофенетических расстояний.

$$ \text{cophCorr} = \frac{\sum\limits_{i < j}(d(x_i, x_j) - \bar{d})(coph(x_i, x_j) - \bar{coph})}{\sqrt{\sum\limits_{i < j}(d(x_i, x_j) - \bar{d})^2 \cdot \sum\limits_{i < j}(coph(x_i, x_j) - \bar{coph})^2}} $$

При "удачно" построенном дереве эти ряды должны сильно коррелировать.

from scipy.spatial.distance import pdist

def coph_demo(link='single', metric='euclidean', k=2):
    
    X, y = make_blobs(n_samples=500,
                  n_features=2,
                  centers=4,
                  cluster_std=1,
                  center_box=(-10.0, 10.0),
                  shuffle=True,
                  random_state=1) 
    
    d = pdist(X, metric=metric)
    
    Z = linkage(X, method=link, metric=metric)
    labels = fcluster(Z,  k, criterion='maxclust')
    
    fig, ax = plt.subplots(1,2)
    
    ax[0].scatter(X[:,0], X[:,1], c=labels)
        
    ax[0].set_xlabel('$x_1$')
    ax[0].set_ylabel('$x_2$')
        
    dend = dendrogram(Z, ax=ax[1], truncate_mode='lastp')   
    coph_corr, coph_dist = cophenet(Z, d)
    
    ax[1].set_title('cophCorr = %.3f' % coph_corr)
    
    plt.show()
    
    

interact(coph_demo, k=IntSlider(min=2, max=10, step=1, value=2), 
         link=['complete', 'single', 'average', 'centroid'], 
         metric=['euclidean', 'cityblock'])

<function __main__.coph_demo(link='single', metric='euclidean', k=2)>

Итог

Преимущества

• Разнообразие критериев
• Любые K из коробки
• Наглядность с дендрограммой

Недостатки

• Требует много ресурсов

Алгоритмы, основанные на плотности

DBSCAN

Хотелось бы...

• Получить кластеры высокой плотности, разделеные участками низкой плотности

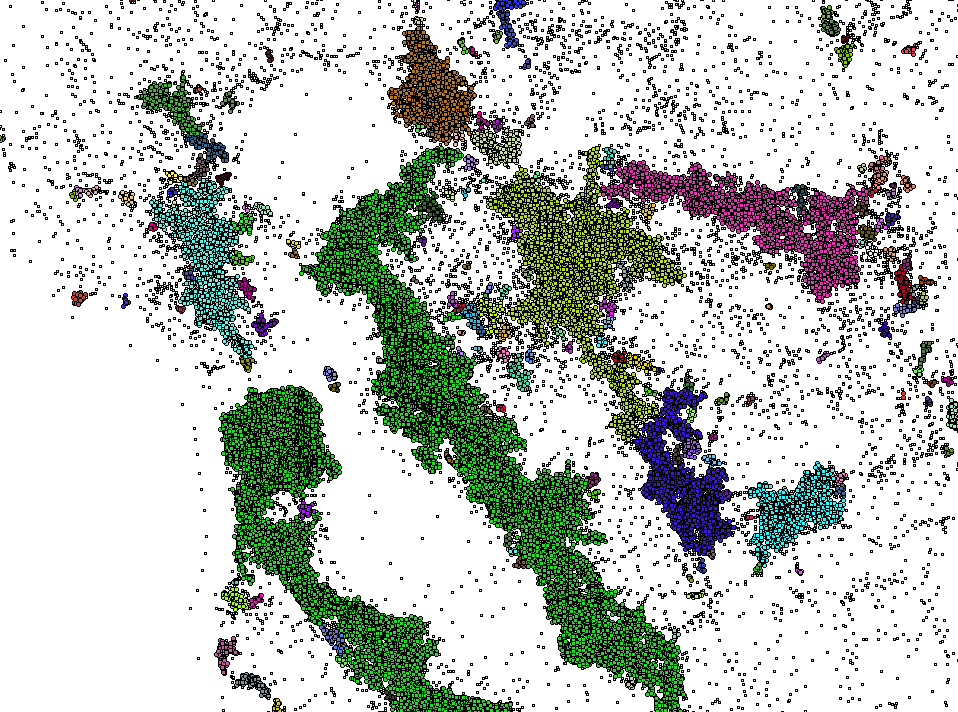
Геоданные

Основная идея

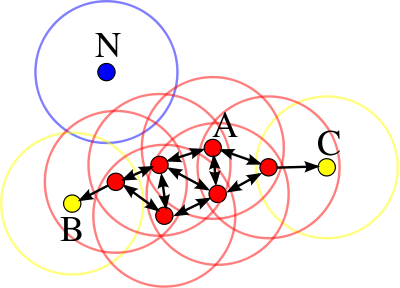
• Для каждой точки кластера её окрестность заданного радиуса $\epsilon$ должна содержать не менее некоторого числа точек min_pts.
• C такой точки можно начать расширение "плотного" кластера

Типы объектов

• Объект $x_i$ называется сore-объектом, если $N_\epsilon(x_i) \geq \texttt{min_pts}$
• Объект $x_i$ называется граничным объектом, если $N_\epsilon(x_i) < \texttt{min_pts}$, но $\exists x_j : d(x_i, x_j) \leq \epsilon$ и $x_j$ - core-объект
• Объект $x_i$ называется шумовым, если он не является ни граничным ни core объектом

Demo

Тык

from sklearn.cluster import DBSCAN


data = np.loadtxt('./data/flame.txt')
X_data = data[:, :2]

def dbscan_demo(eps=1, min_pts=5):
    
    dbscan = DBSCAN(eps=eps, min_samples=min_pts).fit(X_data)
    
    labels = dbscan.labels_
    
    plt.figure(figsize=(7,5))
    plt.scatter(X_data[:,0], X_data[:, 1], c=labels)
    
    plt.show()
    

interact(dbscan_demo, eps=FloatSlider(min=0.1, max=10, step=0.05, value=1), min_pts=IntSlider(min=2, max=15, step=1, value=5))

<function __main__.dbscan_demo(eps=1, min_pts=5)>

Итог

Преимущества

• Не требует $K$
• Кластеры произвольной формы
• Учитывает выбросы

Недостатки

• Не работает при различных плотностях кластеров

Cluster Validity and Quality Measures

Оценка качества кластеризации при известном groud truth

Доля правильно кластеризованных вешин

Пусть $\hat{\pi}$ - это полученное разбиение на кластеры, а $\pi^*$ - ground truth. Тогда доля правильно угаданных меток рассчитывается как

$$ Acc(\hat{\pi}, \pi^*) = \frac{\text{# of correctly clustered obs}}{N} \text{,}$$

где объект считается правильно кластеризован, если хотя бы половина объектов из того же кластера в $\hat{\pi}$ относится к некоторому кластеру в $\pi^*$

Adjusted Rand Index

$$ \text{Rand}(\hat{\pi},\pi^*) = \frac{a + d}{a + b + c + d} \text{,}$$

где

• $a$ - количество пар объектов, находящихся в одинаковых кластерах в $\hat{\pi}$ и $\pi^*$,
• $b$ ($c$) - количество пар объектов в одном и том же кластере в $\hat{\pi}$ ($\pi^*$), но в разных в $\pi^*$ ($\hat{\pi}$)
• $d$ - количество пар объектов в разных кластерах в $\hat{\pi}$ и $\pi^*$

Adjusted Rand Index

$$ \text{Rand}(\hat{\pi},\pi^*) = \frac{tp + tn}{tp + fp + fn + tn} \text{,}$$

где

• $tp$ - количество пар объектов, находящихся в одинаковых кластерах в $\hat{\pi}$ и $\pi^*$,
• $fp$ ($fn$) - количество пар объектов в одном и том же кластере в $\hat{\pi}$ ($\pi^*$), но в разных в $\pi^*$ ($\hat{\pi}$)
• $tn$ - количество пар объектов в разных кластерах в $\hat{\pi}$ и $\pi^*$

Adjusted Rand Index - корректировка Rand index:

$$\text{ARI}(\hat{\pi},\pi^*) = \frac{\text{Rand}(\hat{\pi},\pi^*) - \text{Expected}}{\text{Max} - \text{Expected}}$$

Так же есть Normalized Mutual Information, но результаты этой метрики схожи с ARI

Precision, Recall, F-measure

• $\text{Precision}(\hat{\pi},\pi^*) = \frac{tp}{tp+fn}$
• $\text{Recall}(\hat{\pi},\pi^*) = \frac{tp}{tp+fp}$
• $\text{F-measure}(\hat{\pi},\pi^*) = \frac{2\cdot Precision \cdot Recall}{Precision \cdot Recall}$

Меры валидности кластеров

• Измеряют полученое разбиения по отношению к качествам хорошей кластеризации
  • Компактность объектов внутри кластера
  • Разделимость кластеров друг от друга

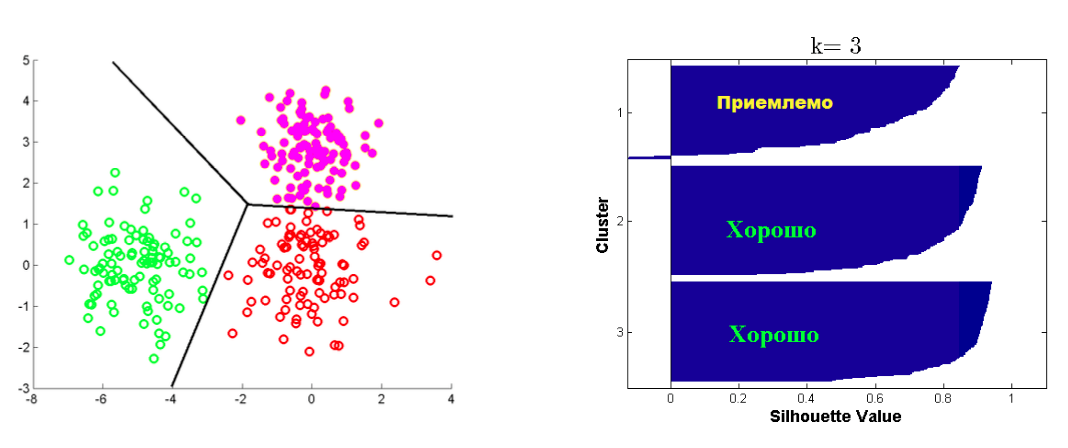
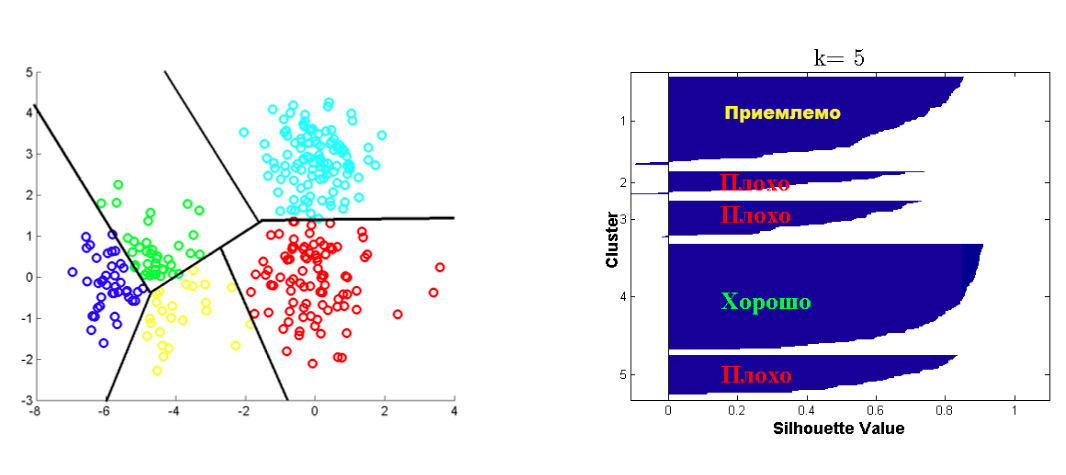
Критерий Silhouette

Пусть дана кластеризация в $K$ кластеров, и объект $i$ попал в $C_k$

• $a(i)$ -- среднее расстояние от $i$ объекта до объектов из $C_k$
• $b(i) = min_{j \neq k} b_j(i)$, где $b_j(i)$ -- среднее расстояние от $i$ объекта до объектов из $C_j$ $$ silhouette(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))} $$ Средний silhouette для всех точек из $\mathbf{X}$ является критерием качества кластеризации.

Литература

• Mohammed J. Zaki, Ch3
• Jure Leskovec, Anand Rajaraman, Jeffrey D. Ullman, Ch7
• Andrew R. Webb, Keith D. Copsey, Ch11