ъ

Методы машинного обучения

 Шестаков Андрей (avshestakov@hse.ru)

---

Методы кластеризации 2

Оценка качества кластеризации

%matplotlib inline

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy

plt.style.use('seaborn-talk')
plt.rcParams['figure.figsize'] = (12,8)

import warnings
warnings.filterwarnings('ignore')

# Для кириллицы на графиках
font = {'family': 'Verdana',
        'weight': 'normal'}
plt.rc('font', **font)

try:
    from ipywidgets import interact, IntSlider, fixed, FloatSlider
except ImportError:
    print(u'Так надо')
    
from IPython.display import YouTubeVideo

/Users/andrey.shestakov/anaconda3/lib/python3.7/importlib/_bootstrap.py:219: RuntimeWarning: numpy.dtype size changed, may indicate binary incompatibility. Expected 96, got 88
  return f(*args, **kwds)

Цели и задача кластеризации

Задача

Основная задача кластерного анализа — разбиение исходного набора объектов на группы (кластеры) таким образом, чтобы:

1. Объекты в группе были похожи друг на друга,
2. Объекты из разных групп - отличались

Цели

• Поиск структуры в данных и ее интерпретация
• Поиск аномальных объектов
• Детальный анализ отдельных кластеров

Алгоритмы, основанные на плотности

DBSCAN

Хотелось бы...

• Получить кластеры высокой плотности, разделеные участками низкой плотности

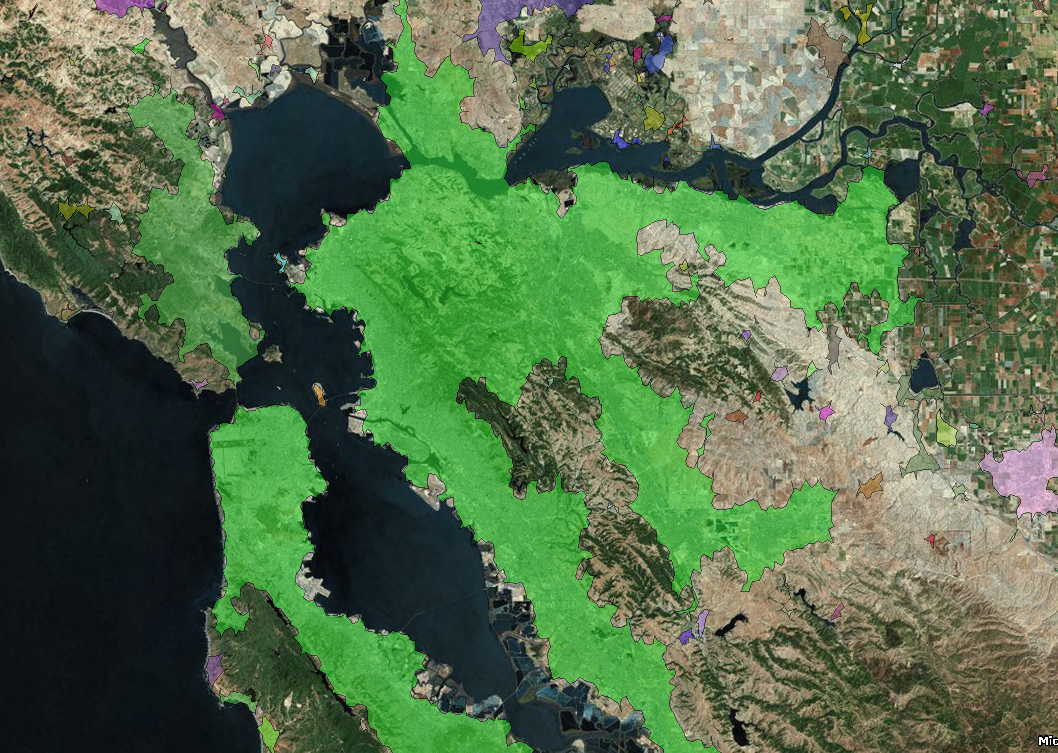
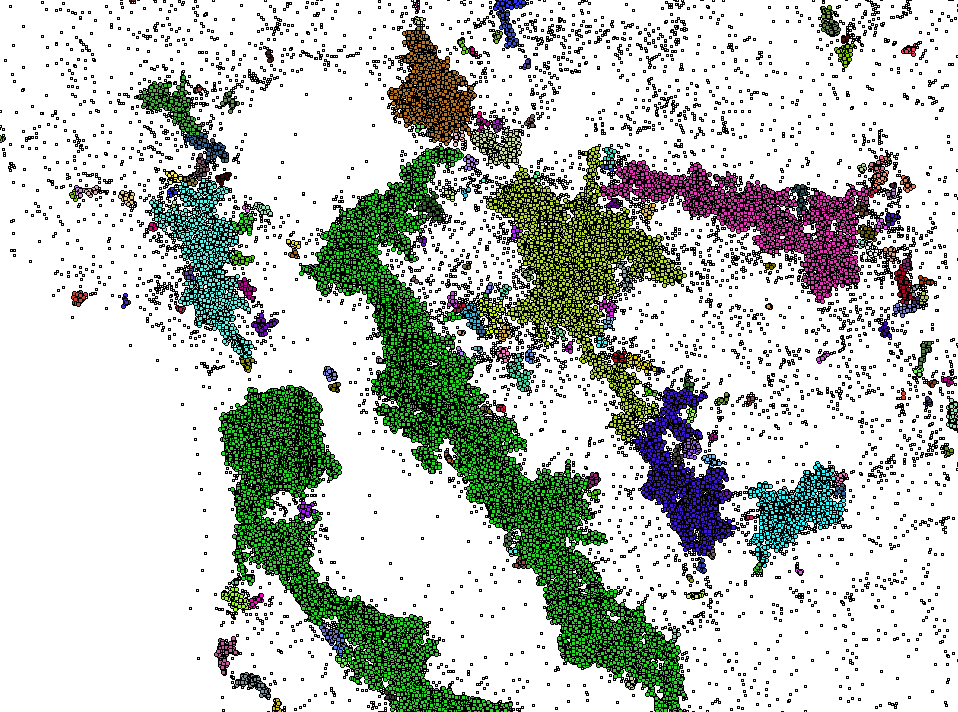
Геоданные

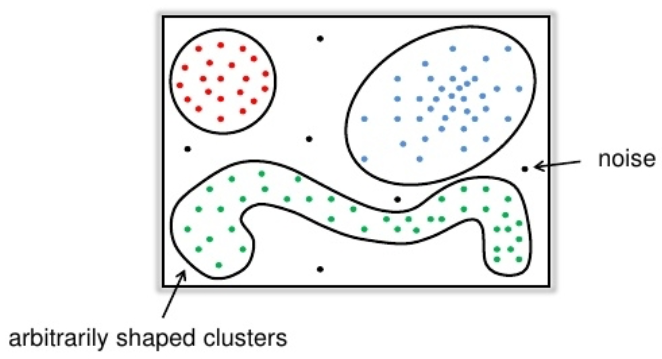
Основная идея

• Для каждой точки кластера её окрестность заданного радиуса $\epsilon$ должна содержать не менее некоторого числа точек min_pts.
• C такой точки можно начать расширение "плотного" кластера

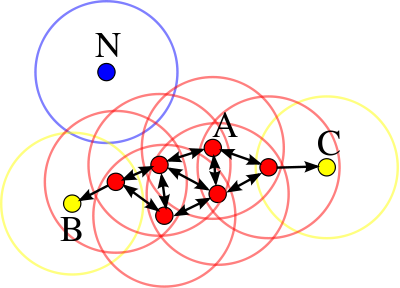
Типы объектов

• Объект $x_i$ называется сore-объектом, если $N_\epsilon(x_i) \geq \texttt{min_pts}$
• Объект $x_i$ называется граничным объектом, если $N_\epsilon(x_i) < \texttt{min_pts}$, но $\exists x_j : d(x_i, x_j) \leq \epsilon$ и $x_j$ - core-объект
• Объект $x_i$ называется шумовым, если он не является ни граничным ни core объектом

Demo

Тык

from sklearn.cluster import DBSCAN


data = np.loadtxt('./data/flame.txt')
X_data = data[:, :2]

def dbscan_demo(eps=1, min_pts=5):
    
    dbscan = DBSCAN(eps=eps, min_samples=min_pts).fit(X_data)
    
    labels = dbscan.labels_
    
    plt.figure(figsize=(7,5))
    plt.scatter(X_data[:,0], X_data[:, 1], c=labels)
    
    plt.show()
    

interact(dbscan_demo, eps=FloatSlider(min=0.1, max=10, step=0.05, value=1), min_pts=IntSlider(min=2, max=15, step=1, value=5))

<function __main__.dbscan_demo>

Итог

Преимущества

• Не требует $K$
• Кластеры произвольной формы
• Учитывает выбросы

Недостатки

• Не работает при различных плотностях кластеров

Модели смеси распределений

Одномерное распределение

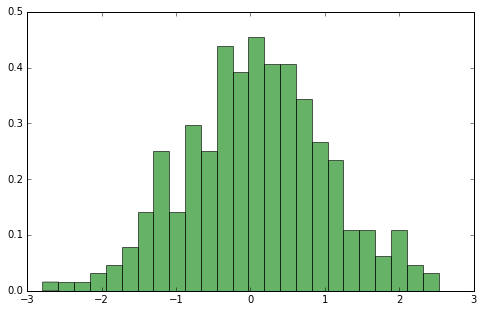
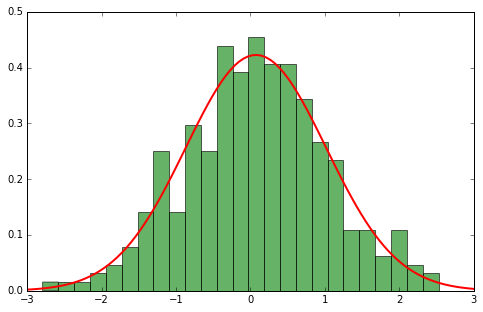
Аппроксимируем параметрическим вероятностным распределением

В одномерном случае $$ p(x | \theta) = \mathcal{N}(x|\mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left({-\frac{(x-\mu)^2}{2\sigma^2}}\right) $$ В многомерном $$ p(x | \theta) = \mathcal{N}(x|\mu, \Sigma) = \frac{1}{(2\pi\Sigma)^{1/2}}\exp\left(-\frac{1}{2}(x-\mu)^\top\Sigma^{-1}(x-\mu)\right) $$

</cetner>

Оценка параметров с помощью ММП

• Рассмотрим логарифм правдоподобия

$$ \begin{align} L(x) = & \prod\limits_{i=1}^B\mathcal{N}(x_i|\mu, \Sigma)\rightarrow \max\limits_{\mu, \Sigma} \end{align} $$

• Возьмем производные и приравняем к 0. Получим оценки параметров

$$\mu_{ML} = \frac 1 N \sum_{i=1}^N x_i, \quad \mathbf{\Sigma}_{ML} = \frac 1 N \sum_{i=1}^N (x_i - \mu_{ML}) (x_i - \mu_{ML})^T$$

А если данные распределены не так тривиально..

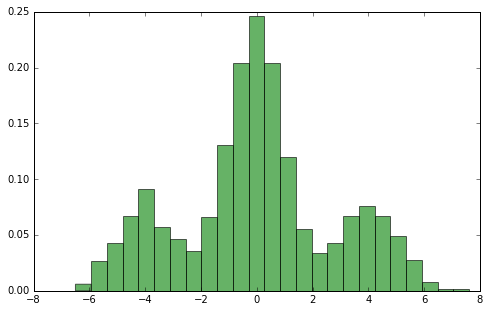</cetner>

Предполагаем СМЕСЬ распределений

$$ p(x)=\sum_{z=1}^{Z}\phi_{z}p(x|\theta_{z}) $$

• $Z$ - Количество компонент
• $\phi_{z},\,z=1,2,...Z$ - выраженность компоненты $z$ в смеси, $\phi_{z}\ge0,\,\sum_{z=1}^{Z}\phi_{z}=1$
• $p(x|\theta_{z})$ - функция плотности распределения
• Параметры смеси $\Theta=\{\phi_{z},\theta_{z},\,z=1,2,...Z\}$

$p(x|\theta_{z})$ могут пренадлежать разным семействам вероятностных распределений

Смесь Гауссовских распределений

$$p(x|\theta_{z})=N(x|\mu_{z},\Sigma_{z}),\,\theta_{z}=\{\mu_{z},\Sigma_{z}\}$$$$ p(x)=\sum_{z=1}^{Z}\phi_{z}N(x|\mu_{z},\Sigma_{z}) $$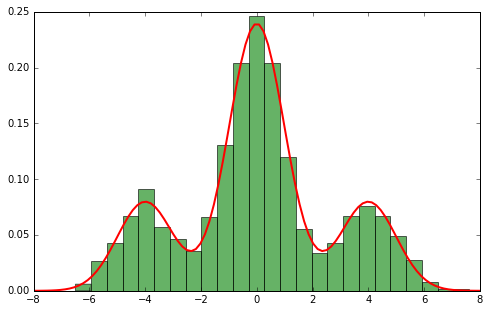

Проблема

• Если рассмотреть логарифм правдоподобия

$$ \begin{align} L(x) = & \sum_{i=1}^N \log p(x_i) = \sum_{i=1}^N\log\left(\sum_{z=1}^{Z}\phi_{z}N(x|\mu_{z},\Sigma_{z})\right) \rightarrow \max\limits_{\mu_z, \Sigma_z, \phi_z} \end{align} $$

• Окажется, что привычными аналитическими методами это не решить
• Будем использовать EM-algorithm!

Reminder: правило Байеса

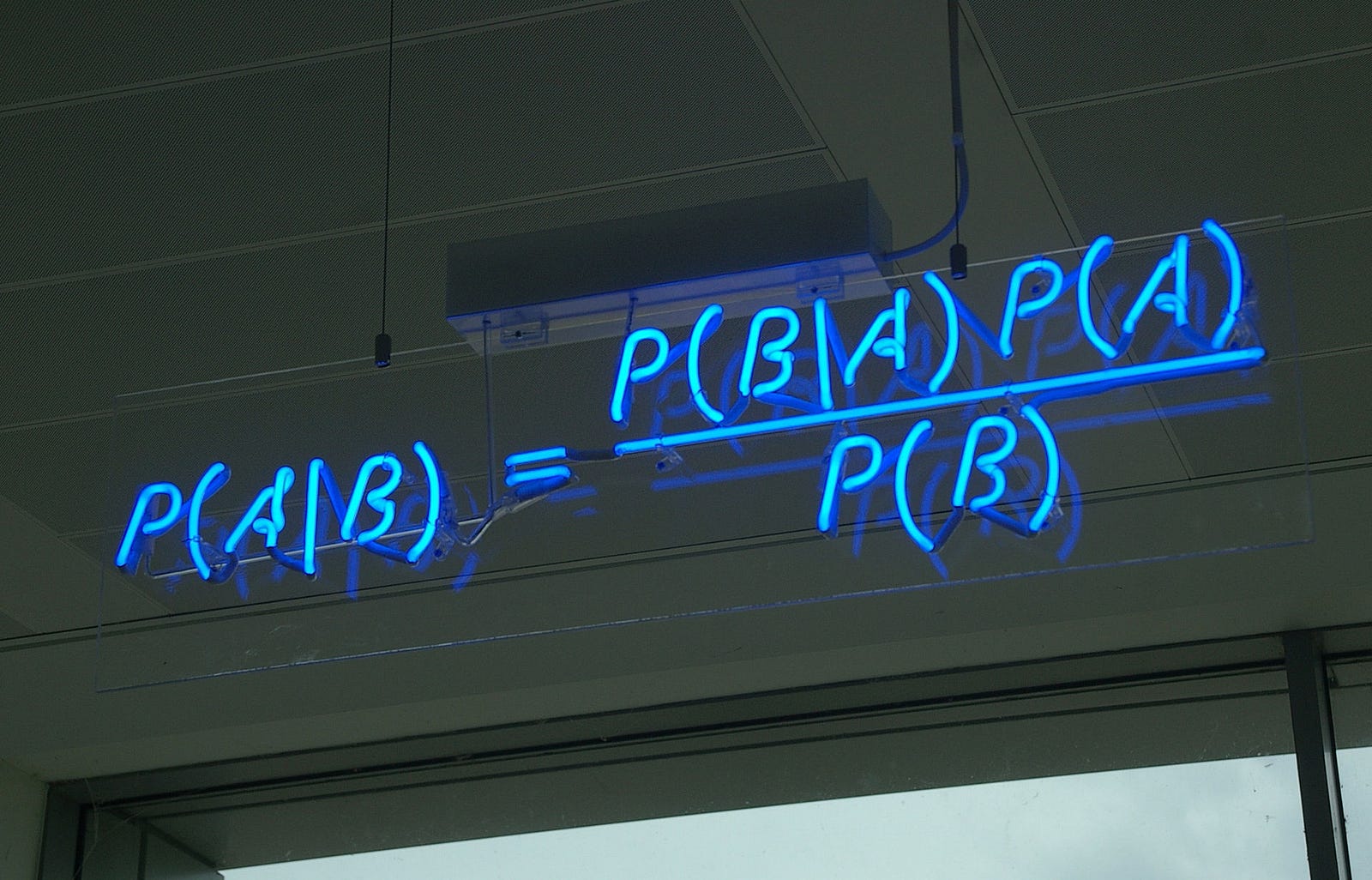
Expectation-Maximization

• Представим, что мы знаем значения параметров $\mu_k$-s, $\Sigma_k$-s и $\phi_k$-s.
• Оценим постериорную вероятность объекта $x_i$ принадлежать компоненте $z$: $$ w_{iz} = p(z | x) = \frac{p(z) p(x_i | z)}{\sum_{k=1}^K p(k) p(x_i | k)} = \frac{\phi_z \mathcal{N}(x_i | \mu_z, \Sigma_z)}{\sum_{k=1}^K \phi_k \mathcal{N}(x_i | \mu_k, \Sigma_k)} $$

$$ \sum_k w_{ik} = 1 $$

• Имея нечеткую принадлежность каждого объекта к каждой компоненте смеси переоценим параметры, максимизирующие правдоподобие: $$ \phi_k = \frac{ \sum_{i=1}^N w_{ik} }{N}, \;\; \mu_k = \frac{\sum_{i=1}^N w_{ik} x_i}{\sum_{i=1}^N w_{ik}} $$ $$ \Sigma_k = \frac {\sum_{i=1}^N w_{ik} (x_i - \mu_k)^\top (x_i - \mu_k)}{\sum_{i=1}^N w_{ik}} $$

Expectation-Maximization

• Похоже на k-средних?

Пример работы

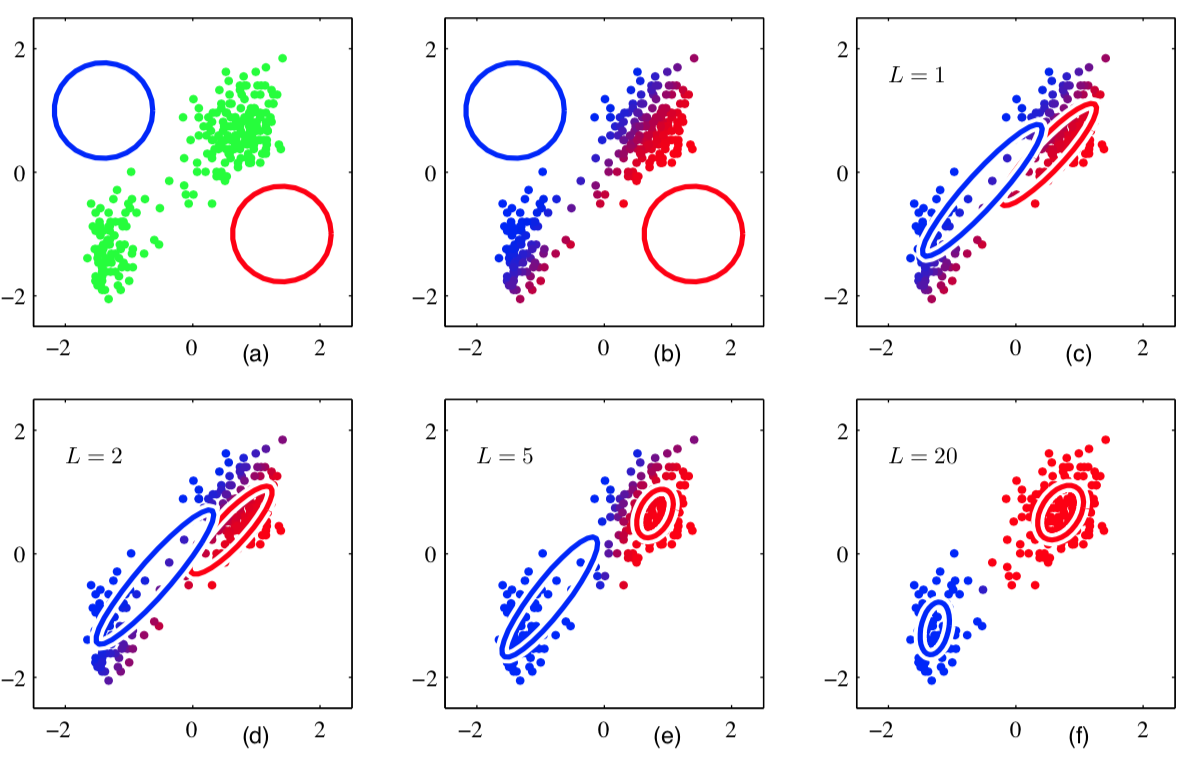
Ограничения на смеси

Ограничения на смеси

• Каждая $\Sigma_{z}\in\mathbb{R}^{DxD}$ содержит $\frac{D(D+1)}{2}$ значений параметров

Смесь без ограничений

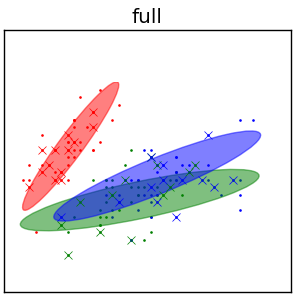
Смесь с одинаковыми \Sigma

• $\Sigma_{1}=\Sigma_{2}=...=\Sigma_{Z}$

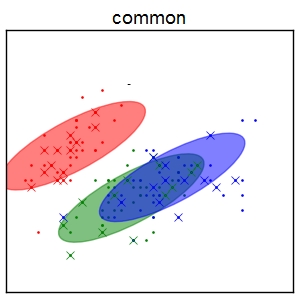
Диагональные $\Sigma$

• $\Sigma_{z}=\text{diag}\{\sigma_{z,1}^{2},\sigma_{z,2}^{2}...\sigma_{z,D}^{2}\}$

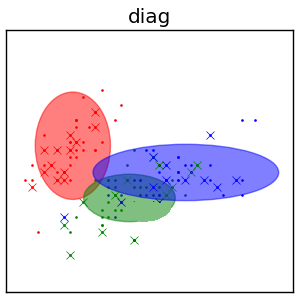
Cферические $\Sigma$

• $\Sigma_{z}=\sigma_{z}^{2}I$,

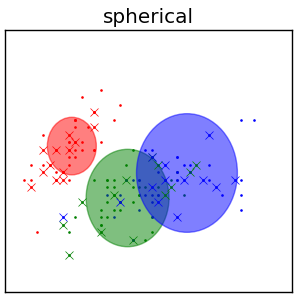
Cluster Validity and Quality Measures

Adjusted Rand Index

$$ \text{Rand}(\hat{\pi},\pi^*) = \frac{a + d}{a + b + c + d} \text{,}$$

где

• $a$ - количество пар объектов, находящихся в одинаковых кластерах в $\hat{\pi}$ и $\pi^*$,
• $b$ ($c$) - количество пар объектов в одном и том же кластере в $\hat{\pi}$ ($\pi^*$), но в разных в $\pi^*$ ($\hat{\pi}$)
• $d$ - количество пар объектов в разных кластерах в $\hat{\pi}$ и $\pi^*$

Adjusted Rand Index

$$ \text{Rand}(\hat{\pi},\pi^*) = \frac{tp + tn}{tp + fp + fn + tn} \text{,}$$

где

• $tp$ - количество пар объектов, находящихся в одинаковых кластерах в $\hat{\pi}$ и $\pi^*$,
• $fp$ ($fn$) - количество пар объектов в одном и том же кластере в $\hat{\pi}$ ($\pi^*$), но в разных в $\pi^*$ ($\hat{\pi}$)
• $tn$ - количество пар объектов в разных кластерах в $\hat{\pi}$ и $\pi^*$

Adjusted Rand Index - корректировка Rand index:

$$\text{ARI}(\hat{\pi},\pi^*) = \frac{\text{Rand}(\hat{\pi},\pi^*) - \text{Expected}}{\text{Max} - \text{Expected}}$$

Precision, Recall, F-measure

• $\text{Precision}(\hat{\pi},\pi^*) = \frac{tp}{tp+fn}$
• $\text{Recall}(\hat{\pi},\pi^*) = \frac{tp}{tp+fp}$
• $\text{F-measure}(\hat{\pi},\pi^*) = \frac{2\cdot Precision \cdot Recall}{Precision \cdot Recall}$

Меры валидности кластеров

• Измеряют полученое разбиения по отношению к качествам хорошей кластеризации
  • Компактность объектов внутри кластера
  • Разделимость кластеров друг от друга

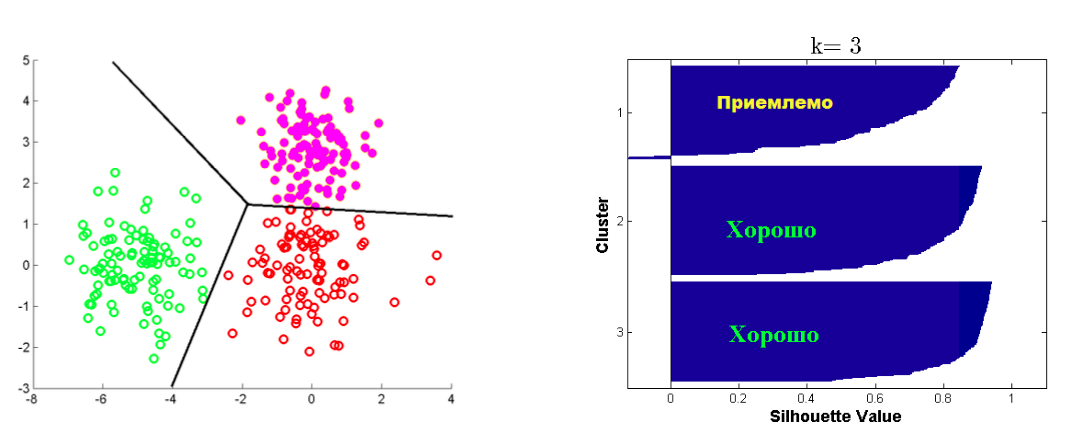
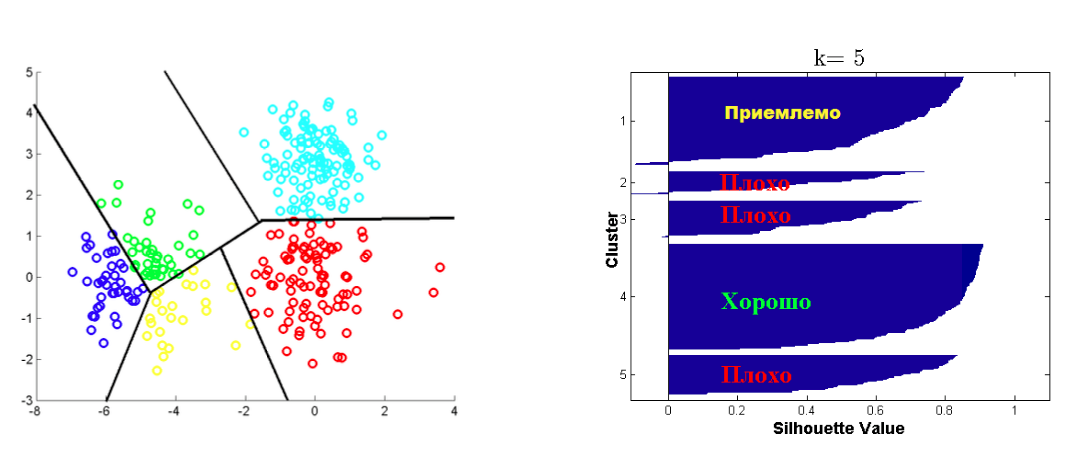
Критерий Silhouette

Пусть дана кластеризация в $K$ кластеров, и объект $i$ попал в $C_k$

• $a(i)$ -- среднее расстояние от $i$ объекта до объектов из $C_k$
• $b(i) = min_{j \neq k} b_j(i)$, где $b_j(i)$ -- среднее расстояние от $i$ объекта до объектов из $C_j$ $$ silhouette(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))} $$ Средний silhouette для всех точек из $\mathbf{X}$ является критерием качества кластеризации.

FYI

• Quality measures review 1
• Quality measures review 2

Литература

• Mohammed J. Zaki, Ch3
• Jure Leskovec, Anand Rajaraman, Jeffrey D. Ullman, Ch7
• Andrew R. Webb, Keith D. Copsey, Ch11