Data Analysis

Andrey Shestakov (avshestakov@hse.ru)

---

Metric-based models¹

Nearest Centroid, K-NN

^{1. Some materials are taken from machine learning course of Victor Kitov}

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

plt.style.use('seaborn-talk')
plt.rcParams['figure.figsize'] = (12,8)

# Для кириллицы на графиках
font = {'family': 'Verdana',
        'weight': 'normal'}
plt.rc('font', **font)

try:
    from ipywidgets import interact, IntSlider, fixed, FloatSlider
except ImportError:
    print u'Так надо'

Let's recall previous lecture

• Machine learning algorithms reconstruct relationship between features $x$ and outputs $y$.
• Design matrix $X=[\mathbf{x}_{1},...\mathbf{x}_{M}]^{T}$, $Y=[y_{1},...y_{M}]^{T}$.
• Relationship is reconstructed by optimal function $\widehat{y}=f_{\widehat{\theta}}(x)$ from function class $\{f_{\theta}(x),\,\theta\in\Theta\}$.
• Empirical risk appriximation
  • Hold-out validation
  • Cross-validation
  • A/B testing
• Given classes $c=1,2,...C$ we may consider discriminant function $g_{c}(x)$ - score of class $c$, given $x$
  • Classification: $\widehat{y}=f(x|\theta)=\arg\max_{c}\left\{ g_{c}(x|\theta)\right\}$

Metric-based models

Cluster hypothesis (Compactness hypothesis)

• the more $x$'s features are similar to ones of $x_i$'s, the more likely $\hat{y}=y_i$

Cluster hypothesis examples

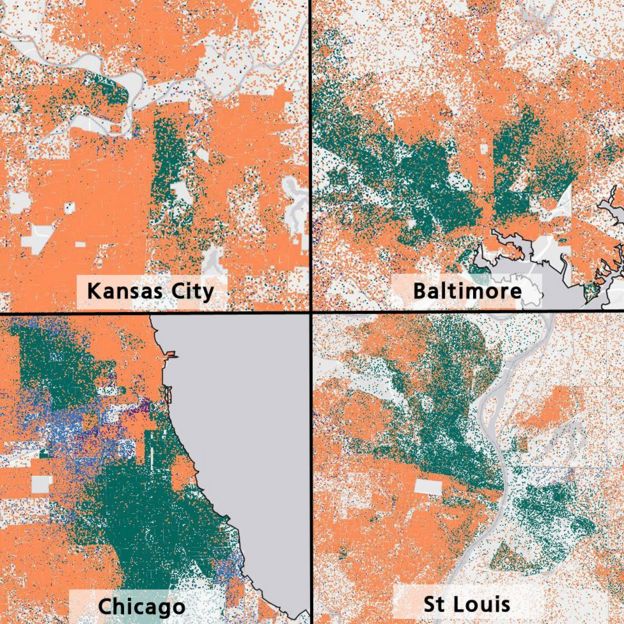
• Objects: Families, households
• Featuers: address, zip code, nearest marketplace... $\rightarrow$ geo-coordinates (lat, lon)
• Target feature: race (classification)

Cluster hypothesis examples

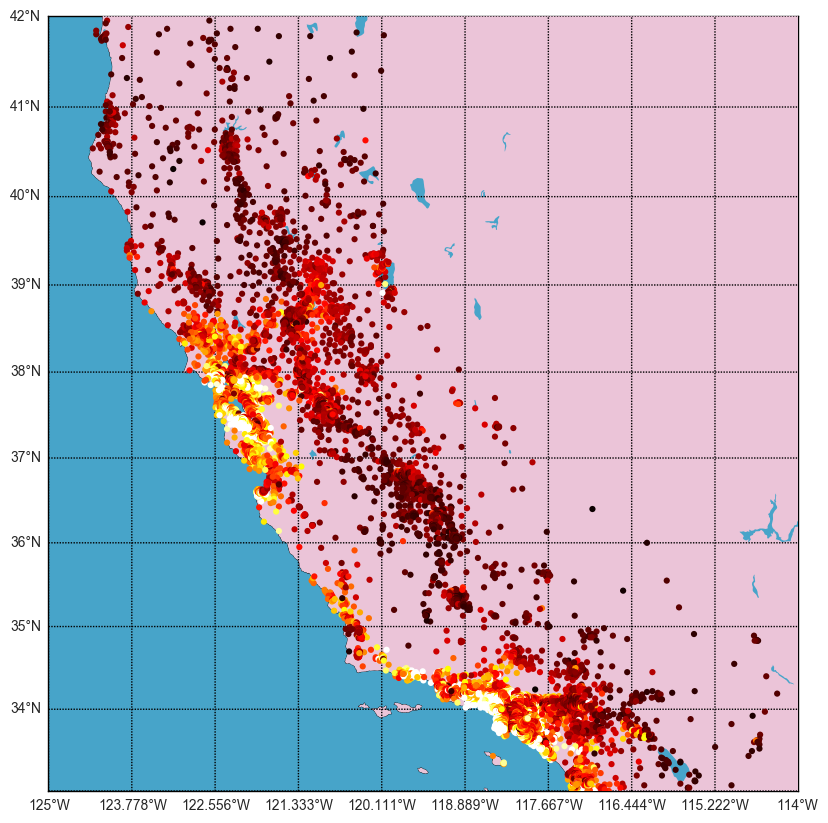
• Objects: Houses
• Features: address... $\rightarrow$ geo-coordinates (lat, lon)
• Target feature: house price (regression)

• Objects: DNA strings
• Features: ??
• Target features: Gene function (classification)

---

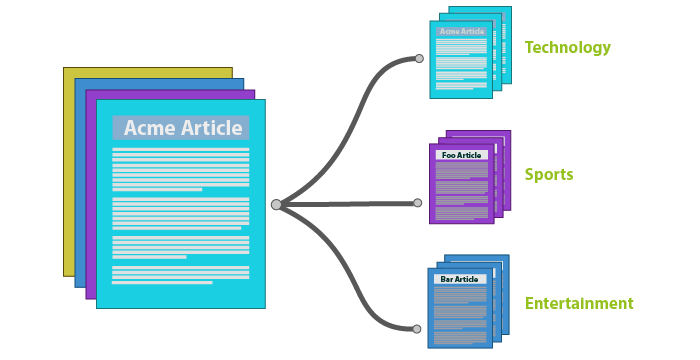
• Objects: Documents, texts, articles
• Features: Word counts
• Target: Document category (classification)

Similarity (distance) measures

Similarity measures

• How do we find similar objects?
• Utilize some similiarity measure (could be metric)

Most popular are

$$ \rho(x_i, x_j) = \sum\limits_{d=1}^{D}(x^d_i - x^d_j)^2 \text{: euclidean distance} $$

$$ \rho(x_i, x_j) = \sum\limits_{d=1}^{D}|x^d_i - x^d_j| \text{: manhattan distance} $$

$$ \rho(x_i, x_j) = 1 - \frac{\langle x_i,x_j \rangle}{||x_i||_2\cdot||x_j||_2} \text{: cosine distance} $$

String Similarity

• Edit distance
  • Number of insertions, replacements and deletions required to modify string $S_1$ to string $S_2$

• Denote $D( i , j )$ as edit distance between substrings $S_1[:i]$ and $S_2[:j]$.
• Use dynamic programming approach to compute $\rho(S_1, S_2):$

\begin{equation} D ( i , j ) = \begin{cases} {\begin{array}{llcl}0,&&&i=0,\ j=0\\i,&&&j=0,\ i>0\\j,&&&i=0,\ j>0\\\min\{\\&D(i,j-1)+1,\\&D(i-1,j)+1,&&j>0,\ i>0\\&D(i-1,j-1)+{\rm {m}}(S_{1}[i],S_{2}[j])\\\}\end{array}}, \end{cases} \end{equation} where $m(a,b) = 0$, if $a = b$ and $1$ otherwise

• Jaro–Winkler distance
• ...

Edit distance example

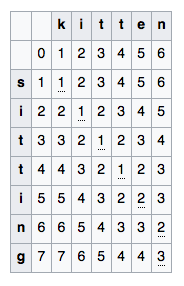
Similarity between sets

• Suppose thet objects are represented with sets
  • Client $a$: {french fries, big-mac, coffe, muffin}
  • Client $b$: {french fries, cheese sause, cheeseburger, coffe, cherry pie}
• Jaccard distance: $$\rho(a,b) = 1 - \frac{|a \cap b|}{|a \cup b|}$$

Nearest Centroid

Nearest centroids algorithm

• Consider training sample $\left(x_{1},y_{1}\right),...\left(x_{N},y_{N}\right)$ with

  • $N_{1}$ representatives of 1st class
  • $N_{2}$ representatives of 2nd class
  • etc.

• Training: Calculate centroids for each class $c=1,2,...C:$ $$ \mu_{c}=\frac{1}{N_{1}}\sum_{n=1}^{N}x_{n}\mathbb{I}[y_{n}=c] $$

• Classification:

  • For object $x$ find the most closest centroid: $$ c=\arg\min_{i}\rho(x,\mu_{i}) $$
  • Associate $x$ the class of the most close centroid: $$ \widehat{y}(x)=c $$

from sklearn.datasets import make_blobs
from sklearn.neighbors import NearestCentroid

def plot_centroid_class():
    
    X_blobs, y_blobs = make_blobs(n_samples=300, n_features=2, centers=4, cluster_std=1.4, random_state=123)
    
    X_centers = np.zeros((4, 2))
    for i in range(4):
        X_centers[i,:] = X_blobs[y_blobs==i,:].mean(axis=0)
    
    plt.scatter(X_blobs[:,0], X_blobs[:,1], c=y_blobs)
    plt.xlabel('$x_1$')
    plt.ylabel('$x_2$')
    
    knn = NearestCentroid()
    knn.fit(X_blobs, y_blobs)
    
    x_range = np.linspace(X_blobs.min(), X_blobs.max(), 500)
    # ОДЗ значений признаков

    xx1, xx2 = np.meshgrid(x_range, x_range)
    
    Y = knn.predict(np.c_[xx1.ravel(), xx2.ravel()])
    Y = Y.reshape(xx1.shape)

    plt.contourf(xx1, xx2, Y, alpha=0.3)
    plt.scatter(X_blobs[:,0], X_blobs[:,1],c=y_blobs, cmap=plt.cm.spectral)
    plt.scatter(X_centers[:, 0], X_centers[:, 1], marker='*', s=400)
    plt.axis('equal')
    plt.show()

Decision boundaries for 4-class nearest centroids}

interact(plot_centroid_class) 

<function __main__.plot_centroid_class>

Questions

• What are discriminant functions $g_{c}(x)$ for nearest centroid?
• What is the complexity for:
  • training?
  • prediction?

• What would be the shape of class separating boundary?
• Can we use similar ideas for regression?
• Is it always possible to have centroids?

K-nearest neighbours (KNN)

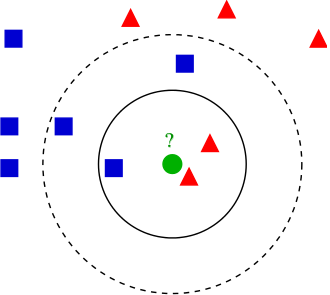
K-nearest neighbours algorithm

Classification:

• Find $k$ closest objects to the predicted object $x$ in the training~set.
• Associate $x$ the most frequent class among its $k$ neighbours.

from sklearn.neighbors import KNeighborsClassifier
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression

from sklearn.datasets import make_moons
X_moons, y_moons = make_moons(noise=0.3, random_state=1234)

plt.scatter(X_moons[:,0], X_moons[:,1], c=y_moons, cmap=plt.cm.spectral)
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')

Text(0,0.5,u'$x_2$')

def plot_knn_class(k=1, prob=False):
    
    plt.scatter(X_moons[:,0], X_moons[:,1], c=y_moons)
    plt.xlabel('$x_1$')
    plt.ylabel('$x_2$')
    
    knn = KNeighborsClassifier(n_neighbors=k, metric='minkowski', p=2)
    knn.fit(X_moons, y_moons)
    
    x_range = np.linspace(X_moons.min(), X_moons.max(), 500)
    # ОДЗ значений признаков

    xx1, xx2 = np.meshgrid(x_range, x_range)
    # всевозможные попарные значения признаков
    if prob:
        Y = knn.predict_proba(np.c_[xx1.ravel(), xx2.ravel()])[:,1]
    else:
        Y = knn.predict(np.c_[xx1.ravel(), xx2.ravel()])
    Y = Y.reshape(xx1.shape)

    plt.contourf(xx1, xx2, Y, alpha=0.3)
    plt.scatter(X_moons[:,0], X_moons[:,1], c=y_moons, cmap=plt.cm.spectral)
    
    plt.show()

interact(plot_knn_class, k=IntSlider(min=1, max=10, value=1))

<function __main__.plot_knn_class>

K-nearest neighbours algorithm

Regression:

• Find $k$ closest objects to the predicted object $x$ in the training~set.
• Associate $x$ average output of its $k$ neighbours.

x_true = np.arange(-5, 5, 0.2)
x = x_true + np.random.rand(x_true.shape[0]) - 0.5
y_true = np.sin(x_true)+x_true/3
y = y_true + np.random.rand(x_true.shape[0]) - 0.5

plt.plot(x_true, y_true, c='g', label='$f(x)$')
plt.scatter(x, y, label='actual data')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=2)

<matplotlib.legend.Legend at 0x1a197da850>

def plot_linreg():
    lin_reg = LinearRegression()
    lin_reg.fit(x.reshape(-1,1), y)
    y_hat = lin_reg.predict(x_true.reshape(-1,1))
    
    plt.plot(x_true, y_true, c='g', label='$f(x)$')
    plt.scatter(x, y, label='actual data')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.plot(x_true, y_hat, c='r', label='linear regression')
    plt.legend(loc=2)

plot_linreg()

def plot_knn(k=1):
    knn = KNeighborsRegressor(n_neighbors=k)
    knn.fit(x.reshape(-1,1), y)
    y_hat = knn.predict(x_true.reshape(-1,1))
    
    plt.plot(x_true, y_true, c='g', label='$f(x)$')
    plt.scatter(x, y, label='actual data')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.plot(x_true, y_hat, c='r', label='knn, $k=%d$' % k)
    plt.legend(loc=2)
    plt.show()
    
    return None

interact(plot_knn, k=IntSlider(min=1, max=10, value=1))

<function __main__.plot_knn>

Comments

• K nearest neighbours algorithm is abbreviated as K-NN.
• $k=1$: nearest neighbour algorithm
• Base assumption of the method:
  • similar objects yield similar outputs

• what is simpler - to train K-NN model or to apply it?

Dealing with similar rank

When several classes get the same rank, we can assign to class:

• with higher prior probability
• having closest representative
• having closest mean of representatives (among nearest neighbours)
• which is more compact, having nearest most distant representative

Parameters and modifications

• Parameters:

* None

• Hyperparameters
  • the number of nearest neighbours $K$
  • distance metric $\rho(x,x')$

• Modifications:
  • forecast rejection option (propose a rule, under what conditions to apply rejection in a) classification b) regression)
  • variable $K$ (propose a method of K-NN with adaptive variable K in different parts of the feature space)

Properties

• Advantages:

  • only similarity between objects is needed, not exact feature values.
    • so it may be applied to objects with arbitrary complex feature description
  • simple to implement
  • interpretable (kind of.. case based reasoning)
  • does not need training
    • may be applied in online scenarios
    • cross-validation may be replaced with LOO.

• Disadvantages:
  • slow classification with complexity $O(NDK)$
  • accuracy deteriorates with the increase of feature space dimensionality (curse of dimentionality)

Special properties

Normalization of features

• Feature scaling affects predictions of K-NN?

Normalization of features

• Feature scaling affects predictions of K-NN?
  • sure it does! Need to normalize
• Equal scaling - equal impact of features
• Non-equal scaling - non-equal impact of features
• Typical normalizations:
  • z-scoring (autoscaling): $$x_{j}'=\frac{x_{j}-\mu_{j}}{\sigma_{j}}$$
  • range scaling: $$x_{j}'=\frac{x_{j}-L_{j}}{U_{j}-L_{j}}$$

where $\mu_{j},\,\sigma_{j},\,L_{j},\,U_{j}$ are mean value, standard deviation, minimum and maximum value of the $j$-th feature.

The curse of dimensionality

• Phenomenon that occures in various fields and have varoius consequences (mainly negative)
• The curse of dimensionality: with growing $D$ data distribution becomes sparse and insufficient.

The curse of dimensionality

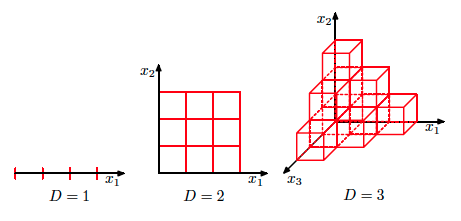
• At what rate should training size grow with increase of $D$ to compensate curse of dimensionality?

The curse of dimensionality

$D=2$	$D=2 \dots 100$

$$ \lim_{D \rightarrow \infty} \frac{\text{dist}_{max} - \text{dist}_{min}}{\text{dist}_{min}} = 0$$

Curse of dimensionality

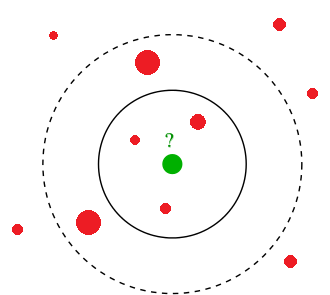
• Case of K-nearest neighbours:
  • assumption: objects are distributed uniformly in unit feature space
  • ball of radius $R$ has volume $V(R)=CR^{D}$, where $C=\frac{\pi^{D/2}}{\Gamma(D/2+1)}$.
  • ratio of volumes of unit cube and included ball: $$ \frac{V(0.5)}{1}=\frac{0.5^{D}\pi^{D/2}}{(D/2)!}\stackrel{D\to\infty}{\longrightarrow}0 $$
  • most of volume concentrates on the corners of the cube
  • nearest neighbours stop being close by distance
• Good news: in real tasks the true dimensionality of the data is often less than $D$ and objects belong to the manifold with smaller dimensionality.

Weighted account

Equal voting

• Consider for object $x$:

  • $x_{i_{1}}$most close neigbour, $x_{i_{2}}$ - second most close neighbour, etc. $$ \rho(x,x_{i_{1}})\le\rho(x,x_{i_{2}})\le...\le\rho(x,x_{i_{N}}) $$

• Classification: $$\begin{align*} g_{c}(x) & =\sum_{k=1}^{K}\mathbb{I}[y_{i_{k}}=c],\quad c=1,2,...C.\\ \widehat{y}(x) & =\arg\max_{c}g_{c}(x) \end{align*} $$

• Regression: $$ \widehat{y}(x)=\frac{1}{K}\sum_{k=1}^{K}y_{i_{k}} $$

Weighted voting

• Weighted classification: $$\begin{align*} g_{c}(x) & =\sum_{k=1}^{K}w(k,\,\rho(x,x_{i_{k}}))\mathbb{I}[y_{i_{k}}=c],\quad c=1,2,...C.\\ \widehat{y}(x) & =\arg\max_{c}g_{c}(x) \end{align*} $$

• Weighted regression: $$ \widehat{y}(x)=\frac{\sum_{k=1}^{K}w(k,\,\rho(x,x_{i_{k}}))y_{i_{k}}}{\sum_{k=1}^{K}w(k,\,\rho(x,x_{i_{k}}))} $$

Commonly chosen weights

Index dependent weights: $$ w_{k}=\alpha^{k},\quad\alpha\in(0,1) $$ $$ w_{k}=\frac{K+1-k}{K} $$

Distance dependent weights:

$$ w_{k}=\begin{cases} \frac{\rho(z_{K},x)-\rho(z_{k},x)}{\rho(z_{K},x)-\rho(z_{1},x)}, & \rho(z_{K},x)\ne\rho(z_{1},x)\\ 1 & \rho(z_{K},x)=\rho(z_{1},x) \end{cases} $$ $$ w_{k}=\frac{1}{\rho(z_{k},x)} $$

Kernels

• $K(\rho, h)$ - some decreasing function
• $h \geq 0$ - parameter (window width)

• gaussian kernel $$K(\rho, h) \propto \exp(- \frac{\rho(x, x')^2}{2h^2})$$
• tophat kernel $$K(\rho, h) \propto 1\ if\ x < h$$
• epanechnikov kernel $$K(\rho, h) \propto 1 - \frac{\rho(x, x')^2}{h^2}$$
• exponential kernel $$K(\rho, h) \propto \exp(-\rho(x, x')/h)$$
• linear kernel $$K(\rho, h) \propto 1 - \rho(x, x')/h\ if\ d < h$$

Kernels

def plot_knn_class_kernel(k=1, h=0.5, prob=False, use_all=False):
    
    def gauss_kernel(d, h=h):
        return np.exp(-(d**2)/(2*h**2))
    
    plt.scatter(X_moons[:,0], X_moons[:,1], c=y_moons)
    plt.xlabel('$x_1$')
    plt.ylabel('$x_2$')
    
    if use_all:
        knn = KNeighborsClassifier(n_neighbors=70, metric='minkowski', p=2, weights=gauss_kernel)
    else:
        knn = KNeighborsClassifier(n_neighbors=k, metric='minkowski', p=2, weights=gauss_kernel)
    knn.fit(X_moons, y_moons)
    
    x_range = np.linspace(X_moons.min(), X_moons.max(), 500)
    # ОДЗ значений признаков

    xx1, xx2 = np.meshgrid(x_range, x_range)
    # всевозможные попарные значения признаков
    if prob:
        Y = knn.predict_proba(np.c_[xx1.ravel(), xx2.ravel()])[:,1]
    else:
        Y = knn.predict(np.c_[xx1.ravel(), xx2.ravel()])
    Y = Y.reshape(xx1.shape)

    plt.contourf(xx1, xx2, Y, alpha=0.3)
    plt.scatter(X_moons[:,0], X_moons[:,1], c=y_moons)
    
    plt.show()

interact(plot_knn_class_kernel, k=IntSlider(min=1, max=10, value=1), 
               h=FloatSlider(min=0.05, max=5, value=1, step=0.05))

<function __main__.plot_knn_class_kernel>

Summary

• Important hyperparameters of K-NN:

  • $K$: controls model complexity
  • $\rho(x,x')$

• Output depends on feature scaling.

  • scaling to equal / non-equal scatter possible.
• Prone to curse of dimensionality.
• Fast training but long prediction.
  • some efficiency improvements are possible though
• Weighted account for objects possible.

FYI

• About Curse of Dimentionality on cats and dogs
• Search optimization benchmarks

Use Case

• Despite being very primitive KNN demonstrated good performance in Facebook's Kaggle competiton
• Competiton page
• Winner interview