Data Analysis

Andrey Shestakov (avshestakov@hse.ru)

Linear regression. Gradient-based optimization¹

^{1. Some materials are taken from machine learning course of Victor Kitov}

Let's recall previous lecture¶

Decision trees
- Utilize the notion of impurity
- Work both for classification and regression
Implicit feature selection
- good for features of different nature
Parallel to axes class separating boundary
Local greedy optimizaion
Sensitive to even tiny data pertubations

Linear regression¶

In [3]:

df_auto.plot(x='mileage', y='price', kind='scatter')

Out[3]:

<matplotlib.axes._subplots.AxesSubplot at 0x110515810>

Linear regression¶

Our goal - determine linear dependence between features $X$ and target vector $y$
Define $X\in\mathbb{R}^{NxD},\{X\}_{ij}$ defines the $j$-th feature of $i$-th object, $y\in\mathbb{R}^{n}$, $y_{i}$ - target value for $i$-th object $$f(x, \beta) = \hat{y} = X\beta \quad \Leftrightarrow \quad f(x_{n}, \beta) = \hat{y}_{n} = \beta_0 + \beta_1x_{n}^1 + \dots$$
Need to estimate $\beta_i$.

Ordinary Lears Squares: $$ L(\beta_0,\beta_1,\dots) = \frac{1}{2N}\sum^{N}_{n=1}(\hat{y}_{n} - y_{n})^2 = \frac{1}{2N}\sum^{N}_{n=1}\left(\sum_{d=1}^{D}\beta_{d}x_{n}^{d}-y_{n}\right)^{2} \rightarrow \min\limits_{\beta} $$ $$ \Updownarrow $$
$$ L(\beta) = \frac{1}{2N}(\hat{y} - y)^{\top}(\hat{y} - y) = \frac{1}{2N}(X\beta - y)^{\top}(X\beta - y) \rightarrow \min\limits_{\beta} $$

Solution¶

Let's say $f(x, \beta) = \beta_0 + \beta_1x_1$

Calculate partial derivatives wrt $\beta_0$, $\beta_1$ and set them to $0$:

$$ \frac{\partial L}{\partial \beta_0} = \frac{1}{N}\sum^{N}_{n=1}(\beta_0 + \beta_1x_{n}^1 - y_{n}) = 0$$ $$ \frac{\partial L}{\partial \beta_1} = \frac{1}{N}\sum^{N}_{n=1}(\beta_0 + \beta_1x_{n}^1 - y_{n})x^1_{n} = 0$$

Solution (in matrix form)¶

Either with matrix calculus or with some linear algebra trick we get

$$ X^{T}(X\beta-y)=0 \quad \Leftrightarrow \quad \beta = (X^\top X)^{-1} X^\top y \quad\text{(Normal Equation)}$$

Comments¶

This is the global minimum, because the optimized criteria is convex.
Geometric interpretation:
- find linear combination of feature measurements that best reproduce $y$
- solution - combinaton of features, giving projection of $y$ on linear span of feature measurements.

Why using Normal Equation could be bad?
- Calculating inverse costs a lot
- Not all matrices have it (singular matrices)

Linearly dependent features (multicollinearity)¶

Solution $\widehat{\beta}=(X^{T}X)^{-1}X^{T}y$ exists when $X^{T}X$ is non-singular
Problem occurs when one of the features is a linear combination of the other (linear dependency)
- because of the property $\forall X:\,rank(X)=rank(X^{T}X)$
- interpretation: non-identifiability of $\widehat{\beta}$ for linearly dependent features:
  - linear dependence: $\exists\alpha:\,x^{T}\alpha=0\,\forall x$
  - suppose $\beta$ solves linear regression $y=x^{T}\beta$
  - then $x^{T}\beta\equiv x^{T}\beta+kx^{T}\alpha\equiv x^{T}(\beta+k\alpha)$, so $\beta+k\alpha$ is also a solution!
Multicollinearity can be exact and not exact, which is also bad

Dummy variable trap!

Linearly dependent features¶

Problem may be solved by:
- feature selection
- dimensionality reduction
- imposing additional requirements on the solution (regularization)

Analysis of linear regression¶

Advantages:

single optimum, which is global (for non-singular matrix)
analytical solution
interpretable solution and algorithm

Drawbacks:

too simple model assumptions (may not be satisfied)
$X^{T}X$ should be non-degenerate (and well-conditioned)

Optimization methods for LR¶

Gradient descent¶

Intuition¶

$$ L(\beta_0, \beta_1) = \frac{1}{2N}\sum_{n=1}^N(\beta_0 + \beta_1x^1_{n} - y_{n})^2$$

Suppose we have some initial approximation of $(\hat{\beta_0}, \hat{\beta_1})$
How should we change it in order to improve?

In [5]:

sq_loss_demo()

Tiny Refresher¶

Derivative of $f(x)$ in $x_0$: $$ f'(x_0) = \lim\limits_{h \rightarrow 0}\frac{f(x_0+h) - f(x_0)}{h}$$

Derivative shows the slope of tangent line in $x_0$

If $x_0$ is extreme point of $f(x)$ and $f'(x_0)$ exists $\Rightarrow$ $f'(x_0) = 0$

In [7]:

interact(deriv_demo, h=FloatSlider(min=0.0001, max=2, step=0.005), x0=FloatSlider(min=1, max=15, step=.2))

Out[7]:

<function __main__.deriv_demo>

Tiny Refresher¶

In multidimential world we switch to gradients and directional derivatives: $$ f'_v(x_0) = \lim\limits_{h \rightarrow 0}\frac{f(x_0+hv) - f(x_0)}{h} = \frac{d}{dh}f(x_{0,1} + hv_1, \dots, x_{0,d} + hv_d) \rvert_{h=0}, \quad ||v|| = 1 \quad \text{directional derivatives}$$

$$ \frac{ \partial f(x_1,x_2,\dots,x_d)}{\partial x_i} = \lim\limits_{h \rightarrow 0}\frac{f(x_1, x_2, \dots, x_i + h, \dots, x_d) - f(x_1, x_2, \dots, x_i, \dots, x_d)}{h} \quad \text{partial derivative}$$

$$ \nabla f = \left(\frac{\partial f}{\partial x_i}\right),\quad i=1\dots d \quad \text{Gradient = a vector of partial derivatives}$$

Tiny Refresher¶

Unsing multivariate chain rule:

$$ f'_v(x_0) = \frac{d}{dh}f(x_{0,1} + hv_1, \dots, x_{0,d} + hv_d) \rvert_{h=0} = \sum_{i=1}^d \frac{\partial f}{\partial x_i} \frac{d}{dh} (x_{0,i} + hv_i) = \langle \nabla f, v \rangle$$

$$ \langle \nabla f, v \rangle = || \nabla f || \cdot ||v|| \cdot \cos{\phi} = || \nabla f || \cdot \cos{\phi}$$

Tiny Refresher¶

$$ \langle \nabla f, v \rangle = || \nabla f || \cdot \cos{\phi}$$

Directional derivative is maximal what direction is collinear to gradient
gradient — direction of steepest ascent of $f(x)$
antigradient — direction of steepest descent of $f(x)$

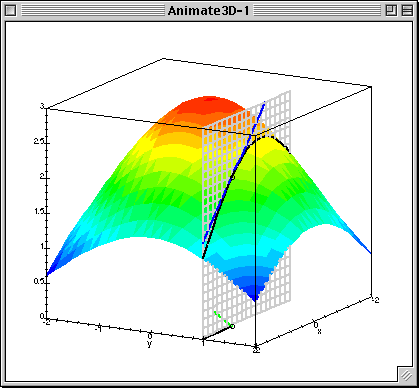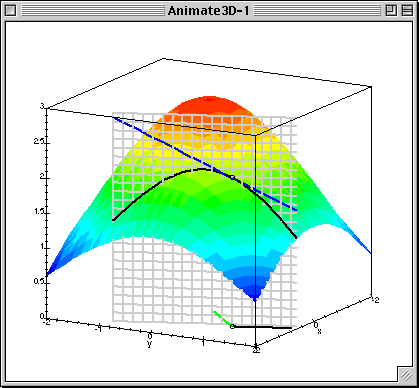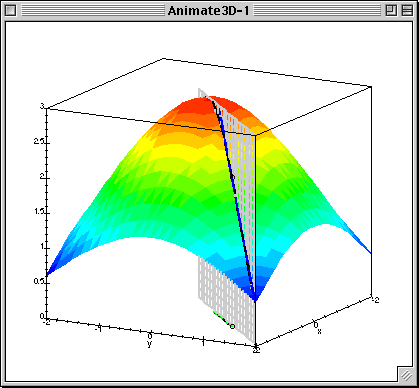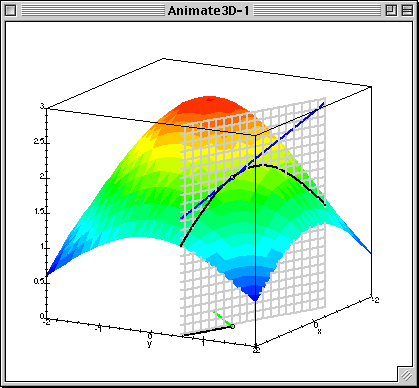
Given $L(\beta_0, \beta_1)$ calculate gradient (patial derivatives) $$ \frac{\partial L}{\partial \beta_0} = \frac{1}{N}\sum^{N}_{i=1}(\beta_0 + \beta_1x_{n}^1 - y^{n})$$ $$ \frac{\partial L}{\partial \beta_1} = \frac{1}{N}\sum^{N}_{i=1}(\beta_0 + \beta_1x_{n}^1 - y^{n})x^1_{n}$$

Or in matrix form: $$ \nabla_{\beta}L(\beta) = \frac{1}{N} X^\top(X\beta - y)$$

Run gradient update, which is simultaneous(!!!) update of $\beta$ in antigradient direction:

$$ \beta := \beta - \alpha\nabla_{\beta}L(\beta)$$

$\alpha$ - descent "speed"

Pseudocode¶

{python}
1.function gd(X, alpha, epsilon):

2.  initialise beta 

3.  do: 

4.      Beta = new_beta

5.      new_Beta = Beta - alpha*grad(X, beta)

6.  until dist(new_beta, beta) < epsilon

7.  return beta

In [9]:

grad_demo(iters=105, alpha=0.08)

Comments¶

How do we set $\alpha$
Feature scales matters
Local minima*

Gradient descent modifications¶

Stochastic gradient descent (!)
Descent with momentum
Adagrad

Methods overview 1, Methods overview 2

Stochastic gradient descent¶

{python}
1.function sgd(X, alpha, epsilon):

2.  initialise beta 

3.  do: 

4.        X = shuffle(X)

5.        for x in X:

6.            Beta = new_beta

7.            new_Beta = Beta - alpha*grad(x, beta)

8.  until dist(new_beta, beta) < epsilon

9.  return beta

In [10]:

stoch_grad_demo(iters=105, alpha=0.08)

Momentum¶

Idea: to move not only to current antigradient direction but consider previous one

$$ v_t = \gamma v_{t - 1} + \alpha\nabla_{\beta}{L(\beta)}$$ $$ \beta = \beta - v_t$$

where

$\gamma$ — momentum term (usually 0.9)

Adagrad¶

Idea: update parameters $\beta_i$ for each feature differenly.

Denote $\frac{\partial L}{\beta_i}$ on iteration $t$ as $g_{t,i}$

Vanilla gd update

$$ \beta_{t+1, i} = \beta_{t, i} - \alpha \cdot g_{t,i}$$

In Adagrad $\alpha$ is normalized wrt "size" of previous derivatives:

$$ \beta_{t+1, i} = \beta_{t, i} - \dfrac{\alpha}{\sqrt{G_{t,ii} + \varepsilon}} \cdot g_{t,i}$$

where $G_t$ is diagonal matrix with sum of squares of derivatives of $\beta_{i}$ before iteration $t$. $\varepsilon$ — is smoothing hyperparameter.

FYI¶

Zero-order methods
- like...
2nd order methods
- Newton method

Nonlinear dependencies¶

Generalization by nonlinear transformations¶

Nonlinearity by $x$ in linear regression may be achieved by applying non-linear transformations to the features:

$$ x\to[\phi_{0}(x),\,\phi_{1}(x),\,\phi_{2}(x),\,...\,\phi_{M}(x)] $$

$$ f(x)=\mathbf{\phi}(x)^{T}\beta=\sum_{m=0}^{M}\beta_{m}\phi_{m}(x) $$

The model remains to be linear in $\beta$, so all advantages of linear regression remain.

Typical transformations¶

$x^{i}\in[a,b]$ : binarization of feature
$x^{i}x^{j}$ : interaction of features
$\exp\left\{ -\gamma\left\lVert x-\tilde{x}\right\rVert ^{2}\right\} $ : closeness to reference point $\tilde{x}$
$\ln x_{k}$ : the alignment of the distribution with heavy tails

In [12]:

demo_weights()

Regularization & restrictions¶

Intuition¶

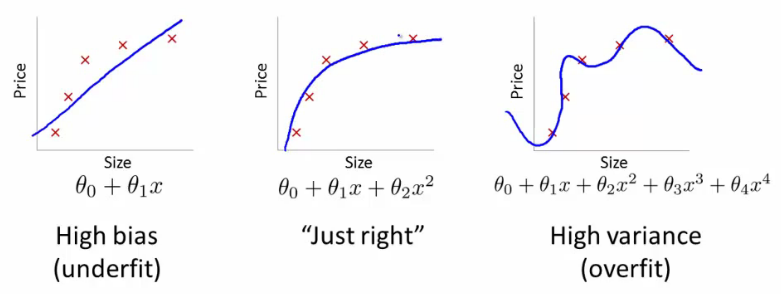
[Andrew's Ng Machine Learning Class - Stanford]

Regularization¶

Insert additional requirement for regularizer $R(\beta)$ to be small: $$ \sum_{n=1}^{N}\left(x_{n}^{T}\beta-y_{n}\right)^{2}+\lambda R(\beta)\to\min_{\beta} $$
$\lambda>0$ - hyperparameter.
$R(\beta)$ penalizes complexity of models. $$ \begin{array}{ll} R(\beta)=||\beta||_{1} & \mbox{Lasso regression}\\ R(\beta)=||\beta||_{2}^{2} & \text{Ridge regression} \end{array} $$

Not only accuracy matters for the solution but also model simplicity!
$\lambda$ controls complexity of the model:$\uparrow\lambda\Leftrightarrow\text{complexity}$$\downarrow$.

Comments¶

Dependency of $\beta$ from $\lambda$ for ridge (A) and LASSO (B):
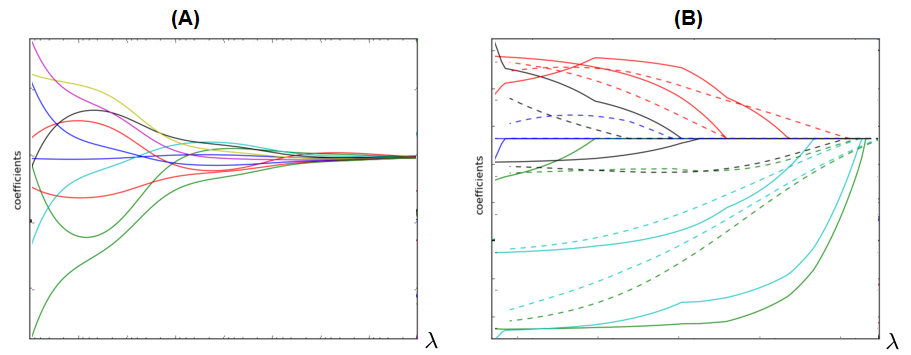
LASSO can be used for automatic feature selection.
$\lambda$ is usually found using cross-validation on exponential grid, e.g. $[10^{-6},10^{-5},...10^{5},10^{6}]$.
It's always recommended to use regularization because
- it gives smooth control over model complexity.
- reduces ambiguity for multiple solutions case.

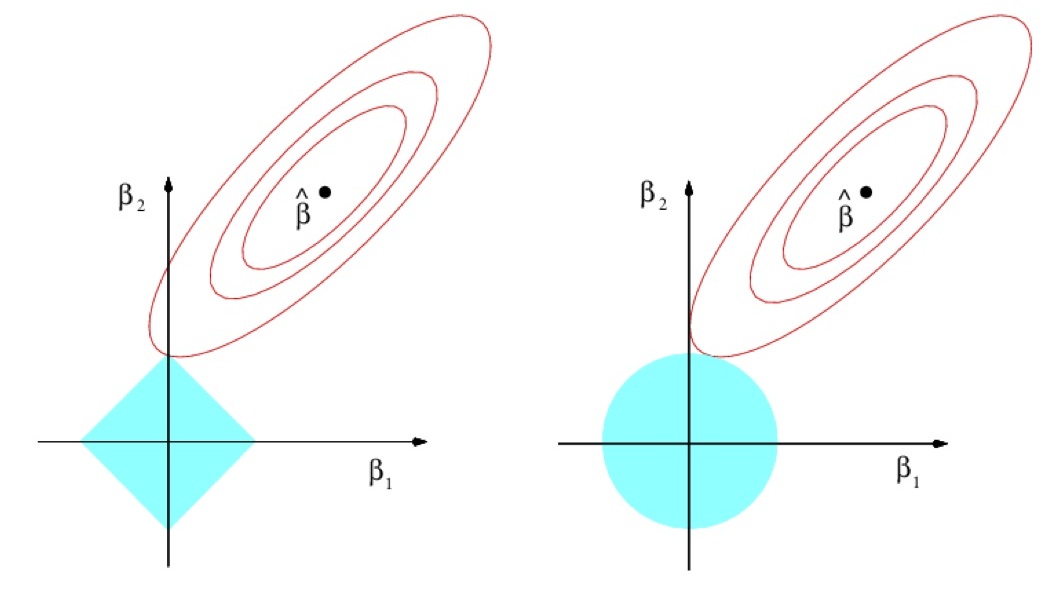
ElasticNet¶

ElasticNet:

$$ R(\beta)=\alpha||\beta||_{1}+(1-\alpha)||\beta||_{2}^{2}\to\min_{\beta} $$ $\alpha\in(0,1)$ - hyperparameter, controlling impact of each part.

If two features $x^{i}$and $x^{j}$ are equal:
- LASSO may take only one of them
- Ridge will take both with equal weight
  - but it doesn't remove useless features
ElasticNet both removes useless features but gives equal weight for usefull equal features
- good, because feature equality may be due to chance on this particular training set

Ridge regression analytic solution¶

Ridge regression criterion $$ \sum_{n=1}^{N}\left(x_{n}^{T}\beta-y_{n}\right)^{2}+\lambda\beta^{T}\beta\to\min_{\beta} $$

Stationarity condition can be written as:

$$ \begin{gathered}2\sum_{n=1}^{N}x_{n}\left(x_{n}^{T}\beta-y_{n}\right)+2\lambda\beta=0\\ 2X^{T}(X\beta-y)+\lambda\beta=0\\ \left(X^{T}X+\lambda I\right)\beta=X^{T}y \end{gathered} $$

$$ \widehat{\beta}=(X^{T}X+\lambda I)^{-1}X^{T}y $$

Comments¶

$X^{T}X+\lambda I$ is always non-degenerate as a sum of:
- non-negative definite $X^{T}X$
- positive definite $\lambda I$

Intuition:
- out of all valid solutions select one giving simplest model
Other regularizations also restrict the set of solutions.

Different account for different features¶

Traditional approach regularizes all features uniformly: $$ \sum_{n=1}^{N}\left(x_{n}^{T}\beta-y_{n}\right)^{2}+\lambda R(\beta)\to\min_{w} $$
Suppose we have $K$ groups of features with indices: $$ I_{1},I_{2},...I_{K} $$
We may control the impact of each group on the model by: $$ \sum_{n=1}^{N}\left(x_{n}^{T}\beta-y_{n}\right)^{2}+\lambda_{1}R(\{\beta_{i}|i\in I_{1}\})+...+\lambda_{K}R(\{\beta_{i}|i\in I_{K}\})\to\min_{w} $$
$\lambda_{1},\lambda_{2},...\lambda_{K}$ can be set using cross-validation
In practice use common regularizer but with different feature scaling.

Different loss-functions¶

Idea¶

Generalize squared to arbitrary loss: $$ \sum_{n=1}^{N}\left(x^{T}\beta-y_{n}\right)^{2}\to\min_{\beta}\qquad\Longrightarrow\qquad\sum_{n=1}^{N}\mathcal{L}(x_{n}^{T}\beta-y_{n})\to\min_{\beta} $$

$$ \begin{array}{lll} \textbf{LOSS} & \textbf{NAME} & \textbf{PROPERTIES}\\ \mathcal{L}(\varepsilon)=\varepsilon^{2} & \text{quadratic} & \text{differentiable}\\ \mathcal{L}(\varepsilon)=\left|\varepsilon\right| & \text{absolute} & \text{robust}\\ \mathcal{L}(\varepsilon)=\begin{cases} \frac{1}{2}\varepsilon^{2}, & \left|\varepsilon\right|\le\delta\\ \delta\left(\left|\varepsilon\right|-\frac{1}{2}\delta\right) & \left|\varepsilon\right|>\delta \end{cases} & \text{Huber} & \text{differentiable, robust} \end{array} $$

Robust means solution is robust to outliers in the training set.

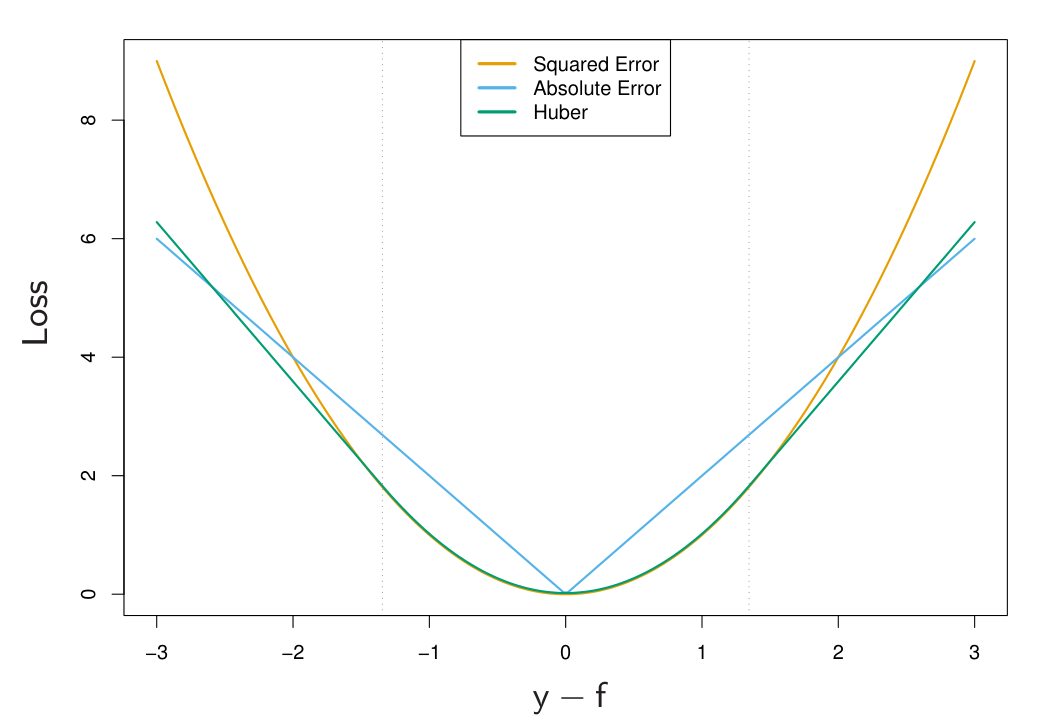
Loss function matters¶

For $y_{1},...y_{N}\in\mathbb{R}$ constant minimizers $\widehat{\mu}$: $$ \begin{align*} \arg\min_{\mu}\sum_{n=1}^{N}(y_{n}-\mu)^{2} & = {\frac{1}{N}\sum_{n=1}^{N}y_{n}}\\ \arg\min_{\mu}\sum_{n=1}^{N}\left|y_{n}-\mu\right| & = {\text{ median}\{y_{1},...y_{N}\}} \end{align*} $$

For $x,y\sim P(x,y)$ and functional minimizers $f(x)$: $$ \begin{align*} \arg\min_{f(x)}\mathbb{E}\left\{ \left.\left(f(x)-y\right)^{2}\right|x\right\} & ={\mathbb{E}[y|x]}\\ \arg\min_{f(x)}\mathbb{E}\left\{ \left.|f(x)-y|\,\right|x\right\} & =\text{median}[y|x] \end{align*} $$

Weighted account for observations¶

Weighted account for observation¶

Weighted account for observations $$ \sum_{n=1}^{N}w_{n}(x_{n}^{T}\beta-y_{n})^{2} $$

Weights may be:
increased for incorrectly predicted objects
- algorithm becomes more oriented on error correction
decreased for incorrectly predicted objects
- they may be considered outliers that break our model

Solution for weighted regression¶

$$ \sum_{n=1}^{N}w_{n}\left(x_{n}^{T}\beta-y_{n}\right)^{2}\to\min_{\beta\in\mathbb{R}} $$

Stationarity condition: $$ \sum_{n=1}^{N}w_{n}x_{n}^{d}\left(x_{n}^{T}\beta-y_{n}\right)=0 $$

Define $\{X\}_{n,d}=x_{n}^{d}$, $W=diag\{w_{1},...x_{N}\}$. Then

$$ X^{T}W\left(X\beta-y\right)=0 $$ $$ \beta=\left(X^{T}WX\right)^{-1}X^{T}Wy $$

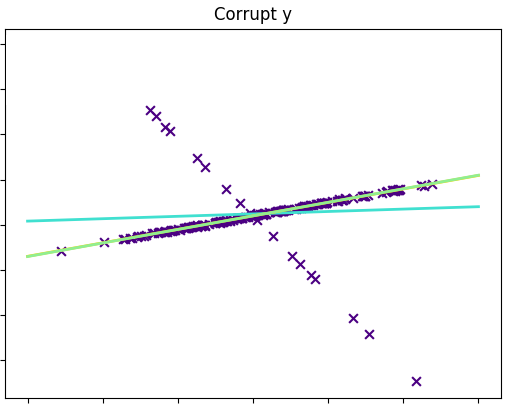
Robust regression¶

Initialize $w_{1}=...=w_{N}=1/N$
Repeat:
- estimate regression $\widehat{y}(x)$ using observations $(x_{i},y_{i})$ with weights $w_{i}$.
- for each $i=1,2,...N$:
  - re-estimate $\varepsilon_{i}=\widehat{y}(x_{i})-y_{i}$
  - recalculate $w_{i}=K\left(\left|\varepsilon_{i}\right|\right)$
- normalize weights $w_{i}=\frac{w_{i}}{\sum_{n=1}^{N}w_{n}}$

Comments: $K(\cdot)$ is some decreasing function, repetition may be

* predefined number of times
* until convergence of model parameters.

Example¶

Nadaraya-Watson regression¶

Minimum squared error estimate¶

For training sample $\left(x_{1},y_{1}\right),...\left(x_{N},y_{N}\right)$ consider finding constant $\widehat{y}\in\mathbb{R}$ $$ L(\alpha)=\sum_{i=1}^{N}(\widehat{y}-y_{i})^{2}\to\min_{\widehat{y}\in\mathbb{R}} $$ $$ \frac{\partial L}{\partial\alpha}=2\sum_{i=1}^{N}\left(\widehat{y}-y_{i}\right)=0\text{, so }\widehat{y}=\frac{1}{N}\sum_{i=1}^{N}y_{i} $$

We need to model general curve $y(x)$:

Nadaraya-Watson regression - localized averaging approach.

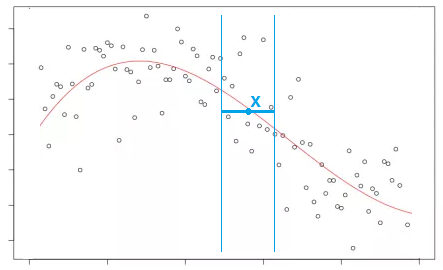
Nadaraya-Watson regression¶

Equivalent names: local constant regression, kernel regression
For each $x$ assume $f(x)=const=\alpha,\,\alpha\in\mathbb{R}$. $$ Q(\alpha,X_{training})=\sum_{i=1}^{N}w_{i}(x)(\alpha-y_{i})^{2}\to\min_{\alpha\in\mathbb{R}} $$
Weights depend on the proximity of training objects to the predicted object:

$$ w_{i}(x)=K\left(\frac{\rho(x,x_{i})}{h}\right) $$

$K(u)$ - some decreasing function, called kernel.
$h(x)$ - some $\ge0$ function called bandwidth.
- Intuition: ``window width'', consider $h(x)=h,\,K(u)=\mathbb{I}[u\le1].$

Parameters¶

Typically used $K(u)$: $$ \begin{eqnarray*} K_{G}(u) & = & e^{-\frac{1}{2}u^{2}}-\text{Gaussian kernel}\\ K_{P}(u) & = & (1-u^{2})^{2}\mathbb{I}[|u|<1]-\text{quartic kernel} \end{eqnarray*} $$
Typically used $h(x)$:
- $h(x)=const$
- $h(x)=\rho(x,x_{i_{K}})$, where $x_{i_{K}}$ - $K$-th nearest neighbour.
  - better for unequal distribution of objects

Solution¶

$$ \begin{align*} Q(\alpha,X_{training}) & =\sum_{i=1}^{N}w_{i}(x)(\alpha-y_{i})^{2}\to\min_{\alpha\in\mathbb{R}}\\ w_{i}(x) & =K\left(\frac{\rho(x,x_{i})}{h(x)}\right) \end{align*} $$

From stationarity condition $\frac{\partial Q}{\partial\alpha}=0$ obtain optimal $\widehat{\alpha}(x)$: $$ f(x,\alpha)=\widehat{\alpha}(x)=\frac{\sum_{i=1}^{N}y_{i}w_{i}(x)}{\sum_{i=1}^{N}w_{i}(x)}=\frac{\sum_{i=1}^{N}y_{i}K\left(\frac{\rho(x,x_{i})}{h(x)}\right)}{\sum_{i=1}^{N}K\left(\frac{\rho(x,x_{i})}{h(x)}\right)} $$

Comments¶

Under general regularity conditions $g(x,\alpha)\overset{P}{\to}E[y|x]$
The specific form of the kernel function does not affect the accuracy much.
- but may affect efficiency

Compared to K-NN: may use all objects, bandwidth controls smoothness

Comments¶

Insead of optimizing locally with constant $\alpha$ $$ Q(\alpha,X_{training})=\sum_{i=1}^{N}w_{i}(x)({\alpha}-y_{i})^{2}\to\min_{\alpha\in\mathbb{R}} $$

we could have optimized local linear regression $$ Q(\alpha,X_{training})=\sum_{i=1}^{N}w_{i}(x)({x^{T}\beta}-y_{i})^{2}\to\min_{\alpha\in\mathbb{R}} $$

This better handles approximation on the edges of domain and local extrema.

Data Analysis

Andrey Shestakov (avshestakov@hse.ru)

Linear regression. Gradient-based optimization1

Let's recall previous lecture¶

Linear regression¶

Linear regression¶

Solution¶

Solution (in matrix form)¶

Comments¶

Linearly dependent features (multicollinearity)¶

Linearly dependent features¶

Analysis of linear regression¶

Optimization methods for LR¶

Gradient descent¶

Intuition¶

Tiny Refresher¶

Tiny Refresher¶

Tiny Refresher¶

Tiny Refresher¶

Pseudocode¶

Comments¶

Gradient descent modifications¶

Stochastic gradient descent¶

Momentum¶

Adagrad¶

FYI¶

Nonlinear dependencies¶

Generalization by nonlinear transformations¶

Typical transformations¶

Regularization & restrictions¶

Intuition¶

Regularization¶

Comments¶

ElasticNet¶

Ridge regression analytic solution¶

Comments¶

Different account for different features¶

Different loss-functions¶

Idea¶

Loss function matters¶

Weighted account for observations¶

Weighted account for observation¶

Solution for weighted regression¶

Robust regression¶

Example¶

Nadaraya-Watson regression¶

Minimum squared error estimate¶

Nadaraya-Watson regression¶

Parameters¶

Solution¶

Comments¶

Comments¶

Linear regression. Gradient-based optimization¹