Data Analysis

Andrey Shestakov (avshestakov@hse.ru)

Supervised learning quality measures¹

^{1. Some materials are taken from machine learning course of Victor Kitov}

Let's recall previous lecture¶

Linear Classification
- Binary linear classifier: $\widehat{y}(x)=sign(w^{T}x+w_{0})$.
- Various multiclassification approaches: 1-vs-all, 1-vs-1, etc..
Perceptron, logistic, SVM - linear classifiers estimated with different loss functions.
Weights are selected to minimize total loss on margins.
Optimized with gradient descent

Quality measures: Regression¶

1. (R)MSE ((Root) Mean Squared Error)

$$ L(\hat{y}, y) = \frac{1}{N}\sum\limits_n^N (y_n - \hat{y}_n)^2$$

2. MAE (Mean Absolute Error)

$$ L(\hat{y}, y) = \frac{1}{N}\sum\limits_n^N |y_n - \hat{y}_n|$$

What are key differences?
What are key issues?

Different scales
MSE penalize greater error more
MAE is robust to outliers
We can compare models with MAE and MSE but it is hard to tell if a model is good overall...

3. RSE (Relative Squared Error)

$$ L(\hat{y}, y) = \sqrt\frac{\sum\limits_n^N (y_n - \hat{y}_n)^2}{\sum\limits_n^N (y_n - \bar{y})^2}$$

4. RAE (Relative Absolute Error)

$$ L(\hat{y}, y) = \frac{\sum\limits_n^N |y_n - \hat{y}_n|}{\sum\limits_n^N |y_n - \bar{y}|}$$

5. MAPE (Mean Absolute Persentage Error)

$$ L(\hat{y}, y) = \frac{100}{N} \sum\limits_n^N\left|\frac{ y_n - \hat{y}_n}{y_n}\right|$$

6. RMSLE (Root Mean Squared Logarithmic Error)

$$ L(\hat{y}, y) = \sqrt{\frac{1}{N}\sum\limits_n^N(\log(y_n + 1) - \log(\hat{y}_n + 1))^2}$$

what is so special about it?

In [25]:

y = 10000
y_hat = np.linspace(0, 30000, 151)
# log error
error1 = np.sqrt((np.log(y+1) - np.log(y_hat + 1))**2)

# squared error
error2 = (y - y_hat)**2 /1000.

plt.plot(y_hat, error1, label='RMSLE')
plt.plot(y_hat, error2, label='MSE')
plt.xlabel('$\hat{y}$')
plt.ylabel('Error')
plt.title('true value y = %.1f' % y)
plt.legend()
plt.ylim(0, 10)

Out[25]:

(0, 10)

Quality measures: Classification¶

Confusion matrix¶

Confusion matrix $M=\{m_{ij}\}_{i,j=1}^{C}$ shows the number of $\omega_{i}$ class objects predicted as belonging to class $\omega_{j}$.

Diagonal elements correspond to correct classifications and off-diagonal elements - to incorrect classifications.

Confusion matrix¶

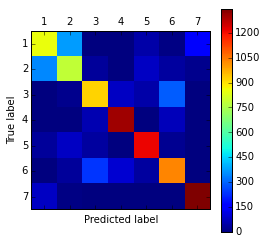
We see here that errors are consentrated between classes 1 and 2
We can
- unite classes 1 and 2 into class "1+2"
- solve 6-class classification problem (instead of 7)
- try to separate classes 1 and 2 afterwards

2 class case¶

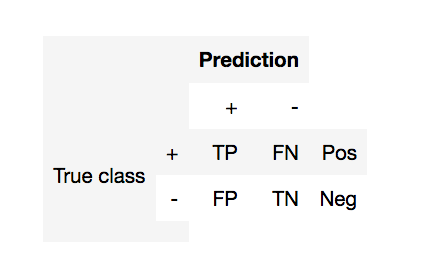
TP (true positive) - currectly predicted positives
FP (false positive) - incorrectly predicted negatives (1st order error)
FN (false negative) - incorrectly predicted positives (2nd order error)
TN (true negative) - currectly predicted negatives
Pos (Neg) - total number of positives (negatives)

2 class case¶

$ \text{accuracy} = \frac{TP + TN}{Pos+Neg}$
$ \text{error rate} = 1 -\text{accuracy}$
$ \text{recall} =\frac{TP}{TP + FN} = \frac{TP}{Pos}$ - (полнота)
$ \text{precision} =\frac{TP}{TP + FP}$ - (точность)
$ \text{F}_\beta \text{-score} = (1 + \beta^2) \cdot \frac{\mathrm{precision} \cdot \mathrm{recall}}{(\beta^2 \cdot \mathrm{precision}) + \mathrm{recall}}$
- why harmonic mean?

What about multiclassification case?

In [18]:

fig = interact(demo_fscore, beta=FloatSlider(min=0.1, max=5, step=0.3, value=1))

Discriminant decision rules¶

Decision rule based on discriminant functions:
- predict $\omega_{1}$ $\Longleftrightarrow$ $g_{1}(x)-g_{2}(x)>\mu$
- predict $\omega_{1}$ $\Longleftrightarrow$ $g_{1}(x)/g_{2}(x)>\mu$ (for $g_{1}(x)>0,\,g_{2}(x)>0$)
Decision rule based on probabilities:
- predict $\omega_{1}$ $\Longleftrightarrow$$P(\omega_{1}|x)>\mu$

Class label versus class probability evaluation¶

Discriminability quality measures} evaluate class label prediction.
- examples: error rate, precision, recall, etc..

Reliability quality measures evaluate class probability prediction.
- Example: probability likelihood: $$ \prod_{i=1}^{N}\widehat{p}(y_{i}|x_{i}) $$
- Brier score: $$ \frac{1}{N}\sum_{n=1}^{N}\sum_{c=1}^{C}\left(\mathbb{I}[y_{n}=c]-\widehat{p}(y=c|x_{n})\right)^{2} $$
- Logloss (cross entropy): $$ \frac{1}{N}\sum_{n=1}^{N}\sum_{c=1}^{C}\mathbb{I}[y_{n}=c]\ln(\widehat{p}(y=c|x_{n})) $$

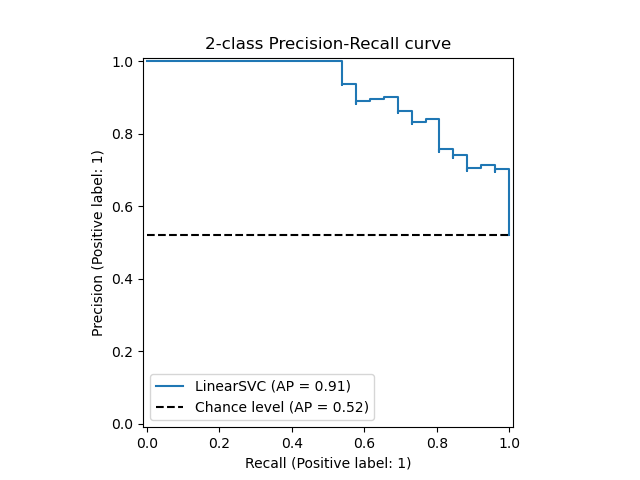
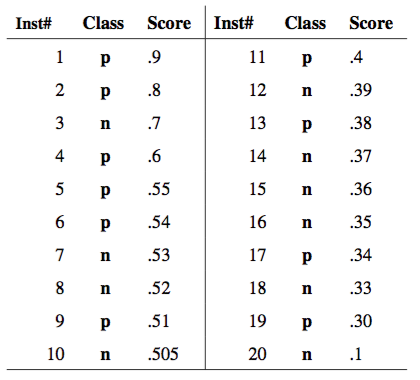
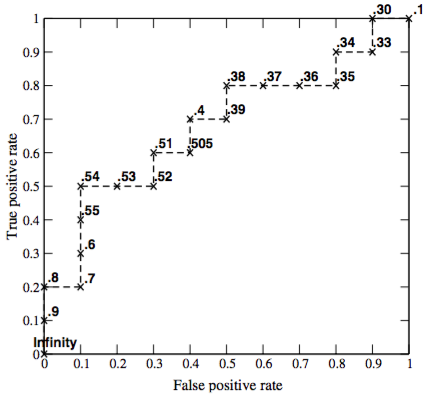
ROC curve¶

ROC curve - is a function TPR(FPR).
It shows how the probability of correct classification on positive classes ("recognition rate") changes with probability of incorrect classification on negative classes ("false alarm").
It is build as a set of points TPR($\mu$), FPR($\mu$).
If $\mu \downarrow$ , the algorithm predicts $\omega_{1}$ more often and
- TPR=$1-\varepsilon_{1}$ $\uparrow$
- FPR=$\varepsilon_{2}$ $\uparrow$
Characterizes classification accuracy for different $\mu$.
- more concave ROC curves are better

$TPR = \frac{TP}{TP + FN}=\frac{TP}{Pos}$, $FPR = \frac{FP}{FP + TN} = \frac{FP}{Neg}$

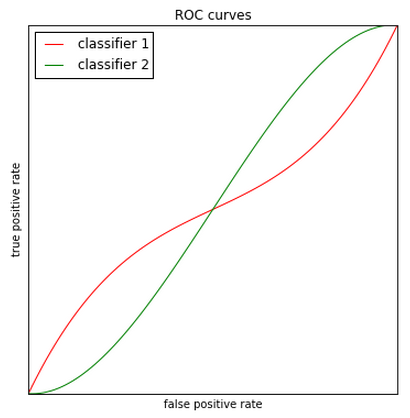
How to compare ROCs?¶

ROC-AUC¶

Area under the ROC curve
Global quality characteristic for different $\mu$
AUC$\in[0,1]$
- AUC = 0.5 - equivalent to random guessing
- AUC = 1 - no errors classification.
AUC property: it is equal to probability that for 2 random objects $x_{1}\in\omega_{1}$ and $x_{2}\in\omega_{2}$ it will hold that: $\widehat{p}(\omega_{1}|x_{1})>\widehat{p}(\omega_{2}|x_2)$
What about unbalanced case?

Precision Recall Curve¶

Build in the same manner as ROC curve
Consider computing PR-AUC

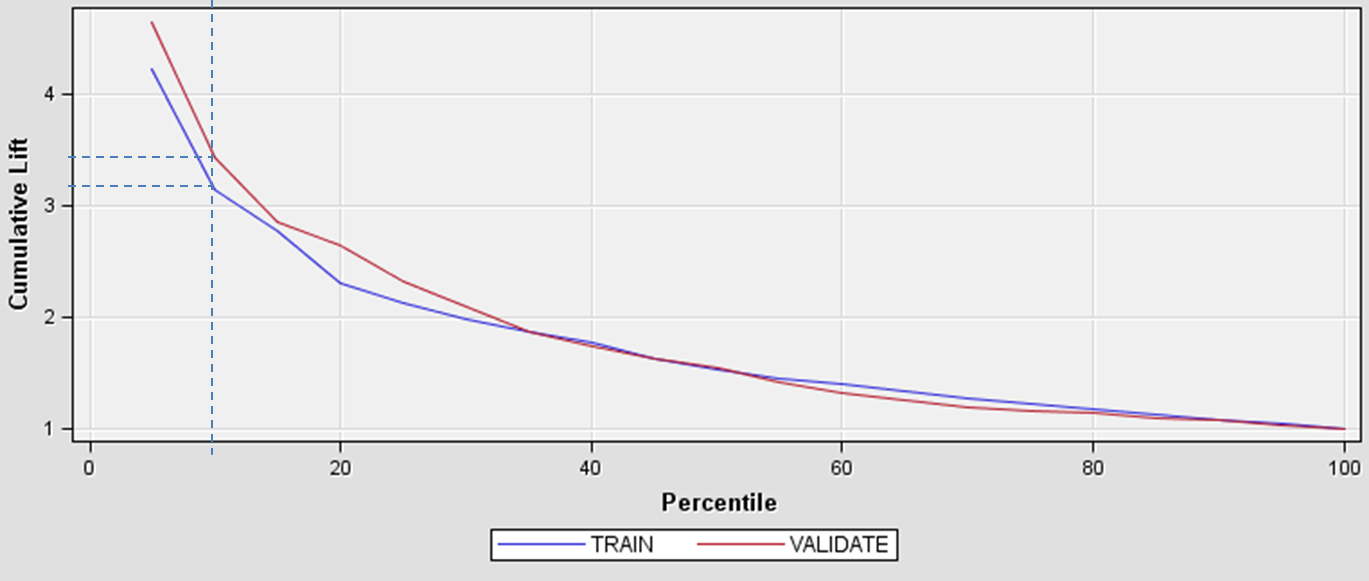
Model Lift¶

Let $r_{POS}$ - positive class rate in the whole dataset
Let $TPR @ K\%$ be positive class rate in top $K \%$ segment of the dateset, sorted by score

$$ Model Lift @ K\% = \frac{TPR @ K\%}{r_{POS}} $$

Unbalanced classification domain¶

Many practical cases consider unbalaced distribution of classes
- Fraud
- Churn
Sometimes quality could be improved via balancing routines

Object weighing¶

$$ \tilde{\mathcal{L}}(X, \theta) = \sum_nw_n\mathcal{L}(x_n, \theta) $$ Usually $w_n$ is inverse-proportional to class ratio of object $x_n$

In [19]:

from sklearn.datasets import make_moons
from imblearn.datasets import make_imbalance
from sklearn.linear_model import LogisticRegression

def demo_weight(class_weight=None, ratio=0.5):

    X_, y_ = make_moons(n_samples=500, shuffle=True, noise=0.3, random_state=0)
    X, y = make_imbalance(X_, y_, ratio, random_state=0)

    model = LogisticRegression(class_weight=class_weight).fit(X, y)
    x0, x1 = np.meshgrid(np.linspace(-1, 2.5, 100),
                         np.linspace(-2, 2, 100))
    xx0, xx1 = x0.ravel(), x1.ravel()

    X_grid = np.c_[xx0, xx1]

    y_hat = model.decision_function(X_grid)
    y_hat = y_hat.reshape(x0.shape)

    plt.contour(x0, x1, y_hat, levels=[0])
    plt.scatter(X[:,0], 
                X[:, 1], 
                c=y, cmap=plt.cm.flag_r)
    plt.axis('equal')

In [20]:

interact(demo_weight, class_weight=['balanced', None], ratio=FloatSlider(min=0.05, max=0.5, step=0.05))

Out[20]:

<function __main__.demo_weight>

Sampling techniques¶

Under-sampling
Over-sampling
Ensemble methods

See imbalanced-learn

Under-sampling¶

Reduce number of majority class

Randomly
Conserving only ethalon objects (ClusterCentroids)
Conserving objects that are close to minor class objects (NearMiss)
Remove objects that have many minor class objects nearby (Condenced NN)

In [21]:

from imblearn.under_sampling import NearMiss, RandomUnderSampler, EditedNearestNeighbours, ClusterCentroids, CondensedNearestNeighbour

def demo_under(ratio=0.5, sampler=None):

    X_, y_ = make_moons(n_samples=500, shuffle=True, noise=0.3, random_state=0)
    X, y = make_imbalance(X_, y_, ratio, random_state=0)
    
    sampler_model = \
              {'rand': RandomUnderSampler(random_state=0),
               'cluster': ClusterCentroids(random_state=0),
               'editnn': EditedNearestNeighbours(random_state=0),
               'condnn': CondensedNearestNeighbour(random_state=0),
               'nearmiss': NearMiss(random_state=0, version=1)}.get(sampler)
    
    if sampler:
        X, y = sampler_model.fit_sample(X, y)

    model = LogisticRegression(class_weight=None).fit(X, y)
    x0, x1 = np.meshgrid(np.linspace(-1, 2.5, 100),
                         np.linspace(-2, 2, 100))
    xx0, xx1 = x0.ravel(), x1.ravel()

    X_grid = np.c_[xx0, xx1]

    y_hat = model.decision_function(X_grid)
    y_hat = y_hat.reshape(x0.shape)

    plt.contour(x0, x1, y_hat, levels=[0])
    plt.scatter(X[:,0], 
                X[:, 1], 
                c=y, cmap=plt.cm.flag_r)
    plt.axis('equal')

In [22]:

interact(demo_under, ratio=FloatSlider(min=0.05, max=0.5, step=0.05), sampler=[None, 'rand', 'cluster', 'editnn', 'condnn', 'nearmiss'])

Out[22]:

<function __main__.demo_under>

Over-sampling¶

Generate move objects from minor class

Randomly
Synthetically

SMOTE¶

Synthetic Minority Over-sampling Technique¶

For each minor class object find $k$ nearest neighbours from the same class
Choose one of them
Generate object(s) between them

In [23]:

from imblearn.over_sampling import SMOTE, RandomOverSampler

def demo_over(ratio=0.5, sampler=None):

    X_, y_ = make_moons(n_samples=500, shuffle=True, noise=0.3, random_state=0)
    X, y = make_imbalance(X_, y_, ratio, random_state=0)
    
    sampler_model = \
              {'rand': RandomOverSampler(random_state=0),
               'smote': SMOTE(),
               }.get(sampler)
    
    if sampler:
        X, y = sampler_model.fit_sample(X, y)

    model = LogisticRegression(class_weight=None).fit(X, y)
    x0, x1 = np.meshgrid(np.linspace(-1, 2.5, 100),
                         np.linspace(-2, 2, 100))
    xx0, xx1 = x0.ravel(), x1.ravel()

    X_grid = np.c_[xx0, xx1]

    y_hat = model.decision_function(X_grid)
    y_hat = y_hat.reshape(x0.shape)

    plt.contour(x0, x1, y_hat, levels=[0])
    plt.scatter(X[:,0], 
                X[:, 1], 
                c=y, cmap=plt.cm.flag_r)
    plt.axis('equal')

In [24]:

interact(demo_over, ratio=FloatSlider(min=0.05, max=0.5, step=0.05), sampler=[None, 'rand', 'smote'])

Out[24]:

<function __main__.demo_over>

Ensemble methods¶

Build and combine models from randomly-balanced datasets

Data Analysis

Andrey Shestakov (avshestakov@hse.ru)

Supervised learning quality measures1

Let's recall previous lecture¶

Quality measures: Regression¶

Quality measures: Classification¶

Confusion matrix¶

Confusion matrix¶

2 class case¶

2 class case¶

Discriminant decision rules¶

Class label versus class probability evaluation¶

ROC curve¶

How to compare ROCs?¶

ROC-AUC¶

Precision Recall Curve¶

Model Lift¶

Unbalanced classification domain¶

Object weighing¶

Sampling techniques¶

Under-sampling¶

Over-sampling¶

SMOTE¶

Synthetic Minority Over-sampling Technique¶

Ensemble methods¶

Useful links¶

Supervised learning quality measures¹