Data Analysis
Andrey Shestakov (avshestakov@hse.ru)
Neural Networks 21
1. Some materials are taken from machine learning course of Victor Kitov
Convolutional Neural Networks¶
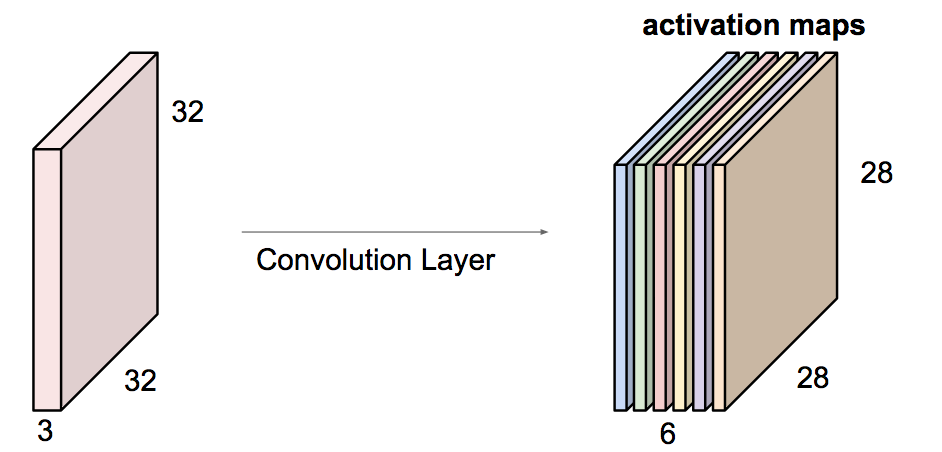
What is image?¶

- Multi-dimentional array
- Key characteristics:
- width
- height
- depth
- range
- Example
- RGB images have depth of 3 (one for each of R, G, B)
- Usually color intencity range is from 0 to 255 (8 bits)
Common Tasks¶
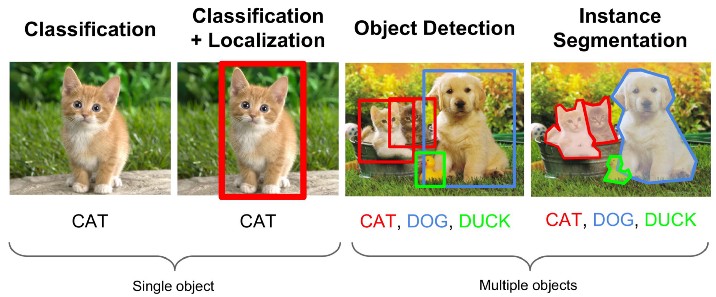
Computer Vision (CV)¶
- There were (are) many things before CNN Hype
Threshold segmentation¶

Threshold segmentation¶

Template Matching¶

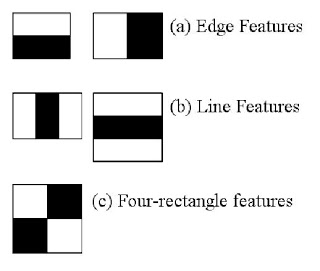
Object Detection with Viola-Jones and Haar¶

It is actually a convolution filter!¶
Result¶

Conv Nets!¶
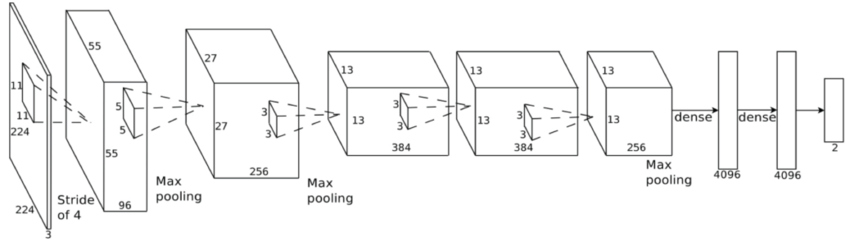
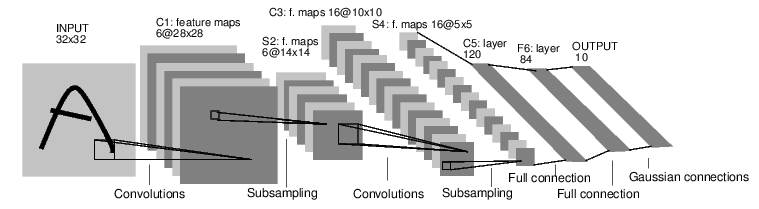
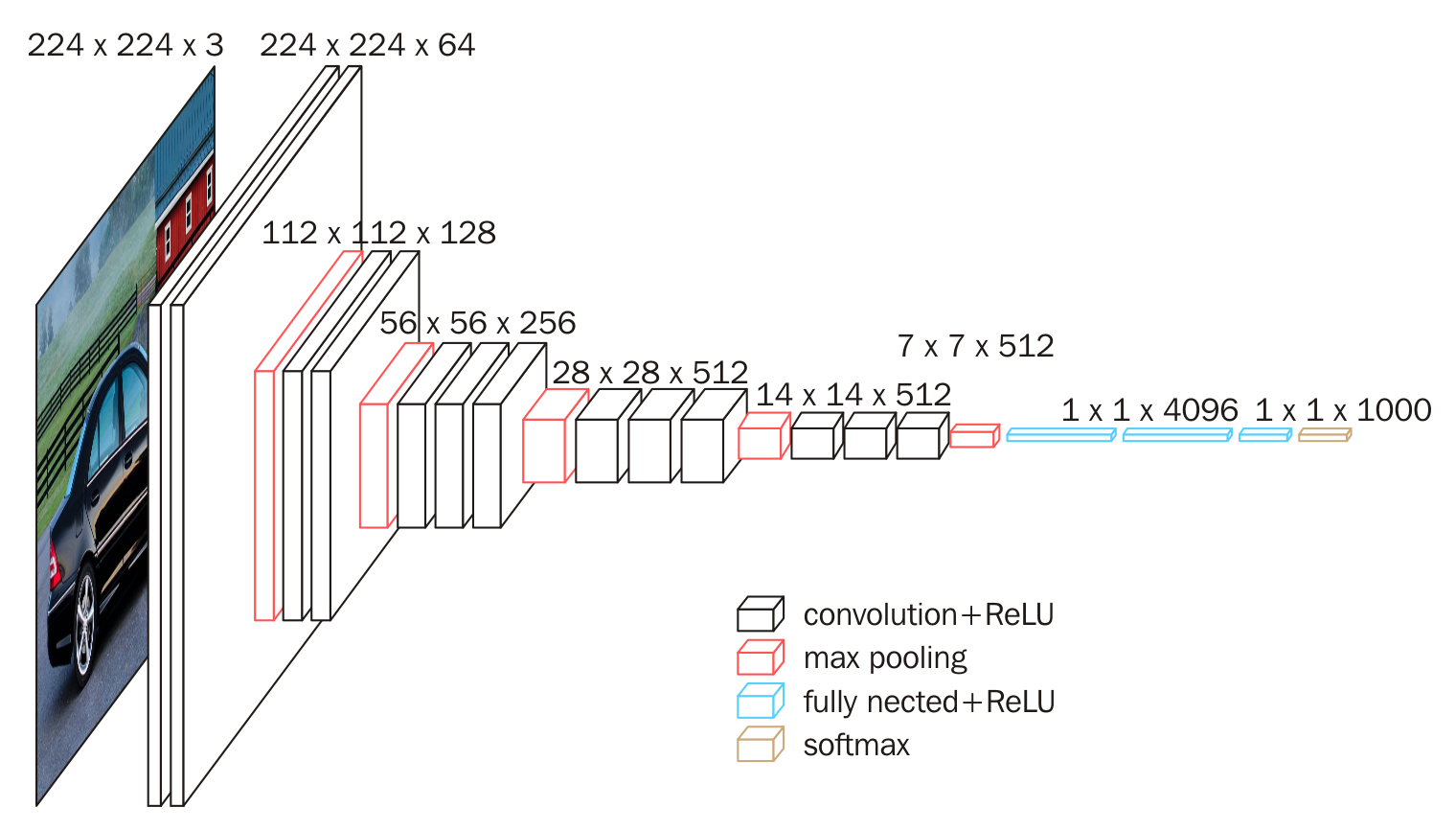
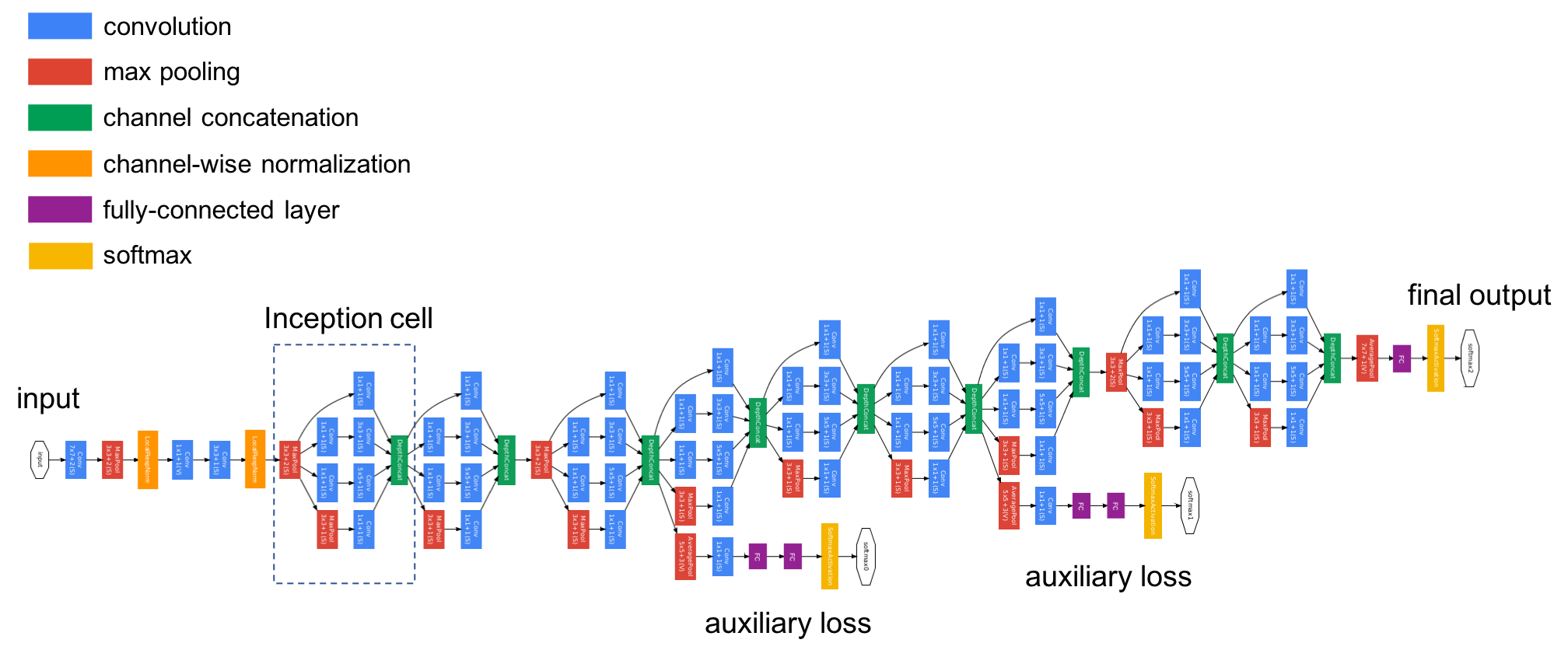
Typical CNN Architecture¶
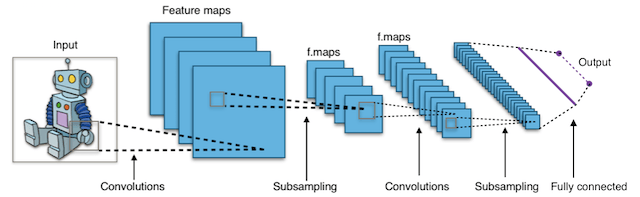
Features¶

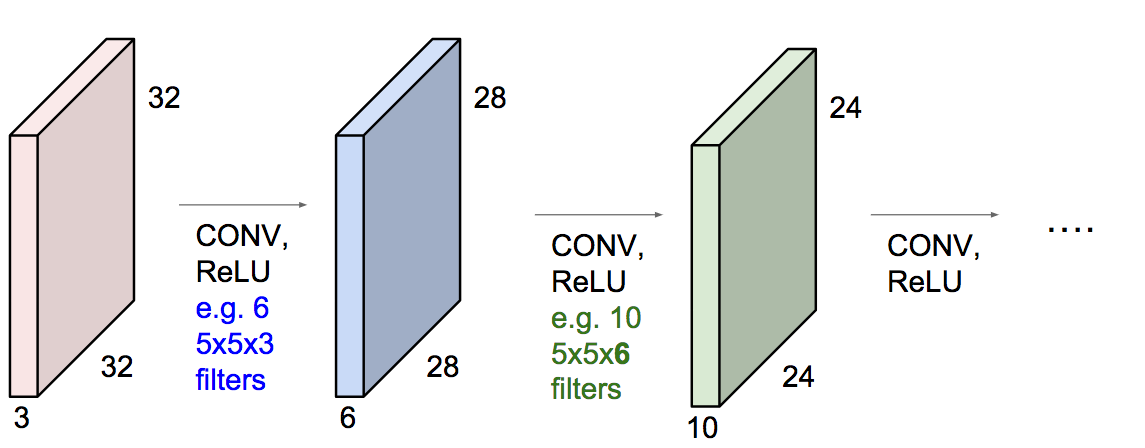
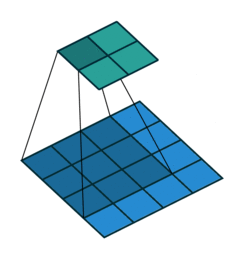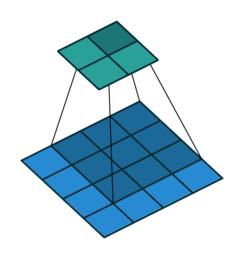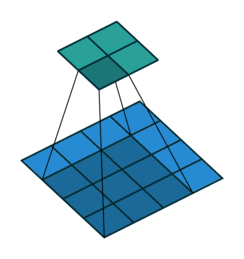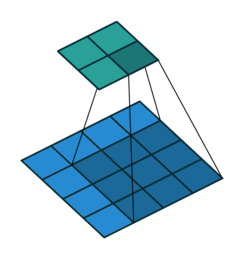
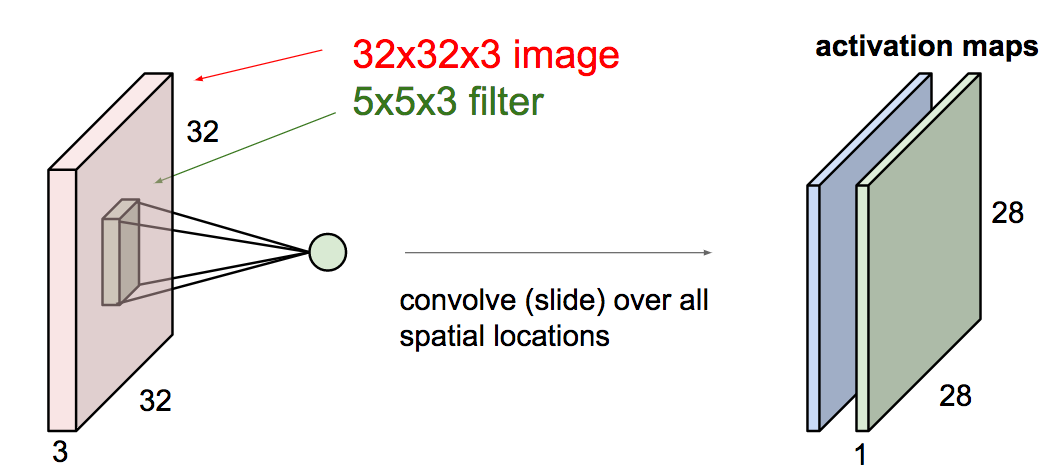
Key Specs of Conv Filters¶
- Number of filters
- Filter Size ($K$)
- Padding Size ($P$)
- Stride Size ($S$)
If number of input features is $N_{in}$ how to calculate number of output features $N_{out}$?
$$N_{out} = \frac{N_{in} + 2P - K}{S} + 1$$
Number of parameters to learn?¶
- Input: $32 \times 32 \times 3$
- $20$ Filters: $5 \times 5$, $P = 1$, $S = 2$
- Number of weights?
$$20\times(5 \times 5 \times 3 + 1) $$
Backprop through convolution¶
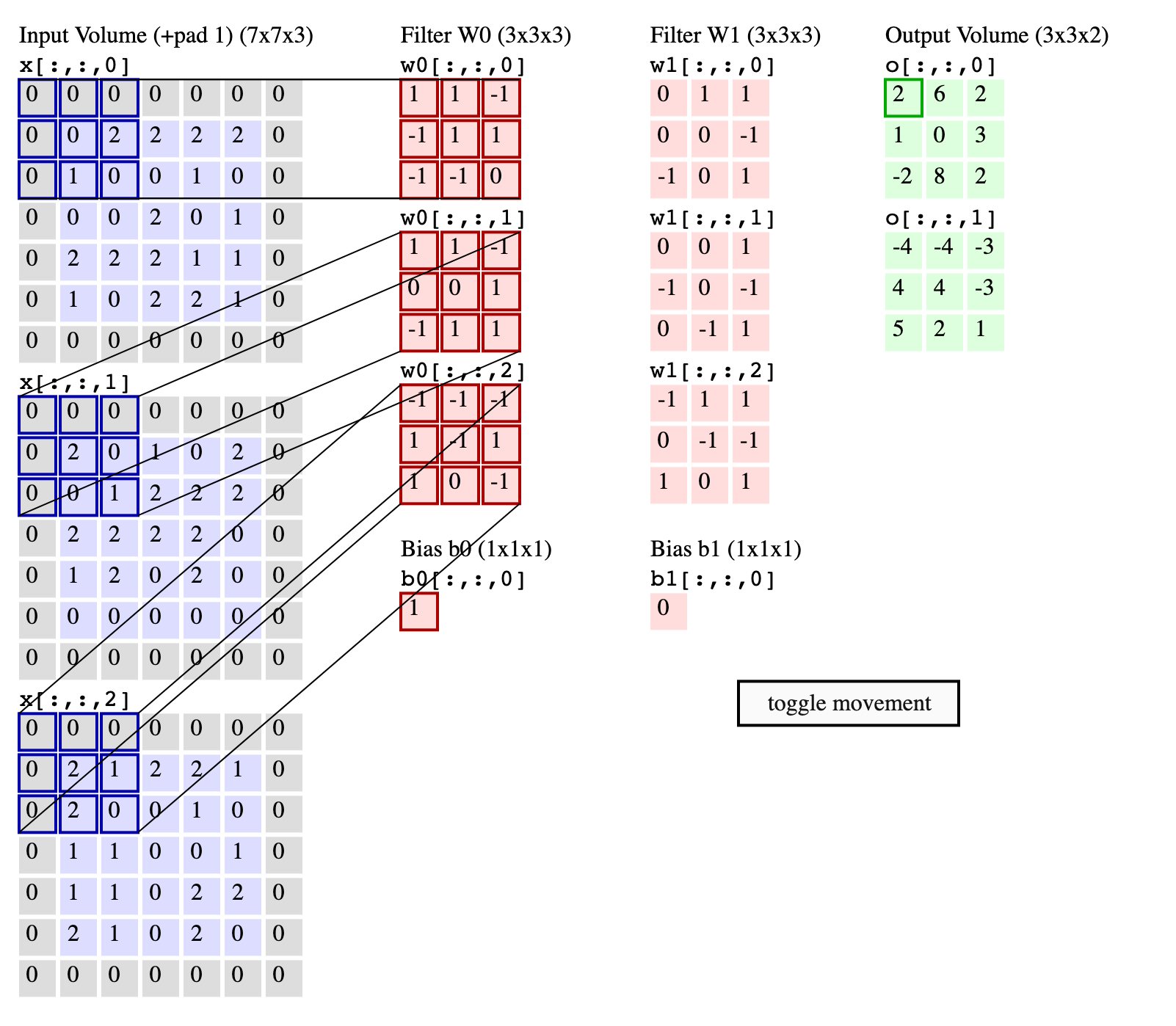
(c) cs231n
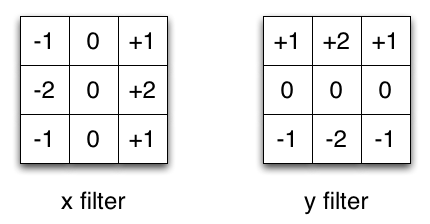
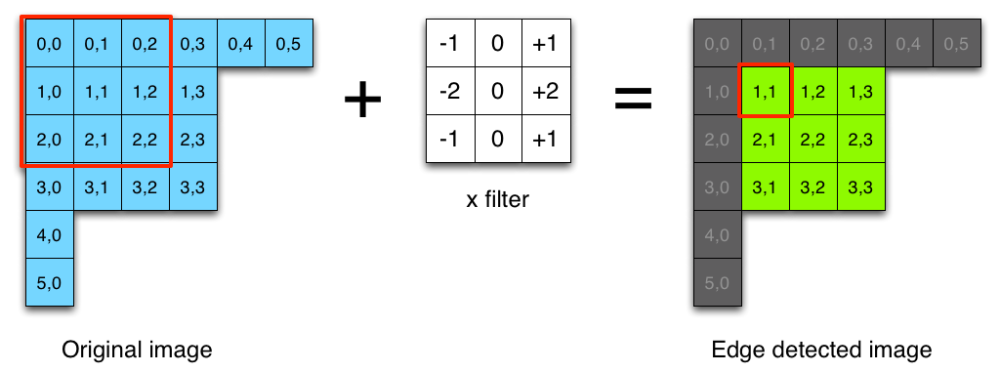
Lets simplify things a bit: consider only a single channel $5 \times 5$ input and $3 \times 3$ convolutional filter.
No strides, no padding, no bias weight.
$$ \begin{align} \left( \begin{array}{ccccc} 0 & 1 & 2 & 1 & 0 \\ 4 & 1 & 0 & 1 & 0 \\ 2 & 0 & 1 & 1 & 1 \\ 1 & 2 & 3 & 1 & 0 \\ 0 & 4 & 3 & 2 & 0 \\ \end{array} \right) &\quad * & \left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 2 & 1 & 0 \\ \end{array} \right) & \quad = & \left( \begin{array}{ccc} 9 & 5 & 4 \\ 8 & 8 & 10 \\ 8 & 15 & 12 \\ \end{array} \right) \\ \mathbf{X} \qquad \qquad &\quad * & \mathbf{W} \qquad & \quad = & \mathbf{I} \qquad \end{align} $$Denote
- $I_{i,j}$ - input $(i,j)$-th element of feature map ("neuron")
- $O_{i,j}$ - "activated" $(i,j)$-th element of feature map ("neuron")
Go down to indices (filter indexing starts from "center"):
$$ I_{i,j} = \sum\limits_{-1 \leq a,b \leq 1} W_{a,b}X_{i+a, j+b} $$And usually some activation function $f(\cdot)$ is applied: $$ O_{i,j} = f(I_{i,j}) $$
Similarly to backprop algorithm in previous lecture:
- Define $\delta_{i,j}$ as error in $(i,j)$ position of feature map: $$ \delta_{i,j} = \frac{\partial L}{\partial I_{i,j}} = \frac{\partial L}{\partial O_{i,j}}\frac{\partial O_{i,j}}{\partial I_{i,j}} = \frac{\partial L}{\partial O_{i,j}} f'(I_{i,j}) $$
- To compute $\frac{\partial L}{\partial W_{a,b}}$ we have to take into account that weight as "shared" $$\frac{\partial L}{\partial W_{a,b}} = \sum_i \sum_j \frac{\partial L}{\partial I_{i,j}} \frac{\partial I_{i,j}}{\partial W_{a,b}} = \sum_i \sum_j \delta_{i,j} X_{i+a, j+b}$$
- Finally, to pass gradients to previous layers: $$\frac{\partial L}{\partial X_{i,j}} = \sum_{a,b} \frac{\partial L}{\partial I_{i-a, j-b}} \frac{\partial I_{i-a, j-b}}{\partial X_{i, j}} = \sum_{a,b} \delta_{i-a,j-b} W_{a,b}$$
OMG, it is convolution too!
Pooling layers¶
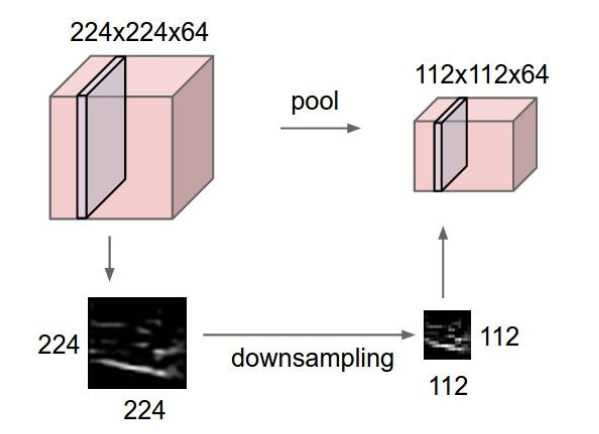
Pooling layers¶
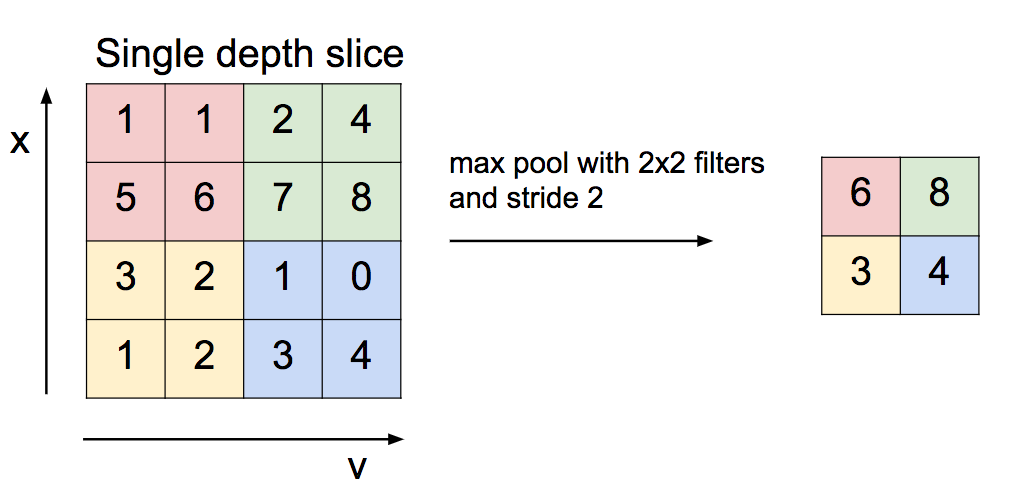
What's with derivative here?
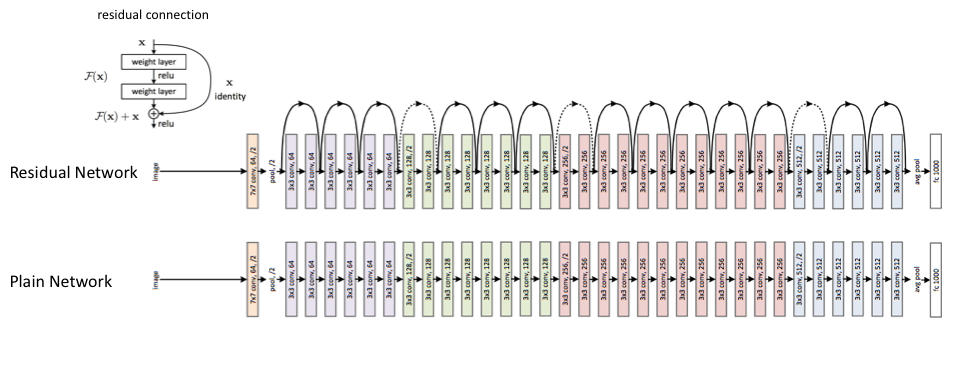
Common Architectures¶
Other things to know¶
Dropout technique¶
- Have L1 and L2 regularization for weights
- Can complement it with Dropout
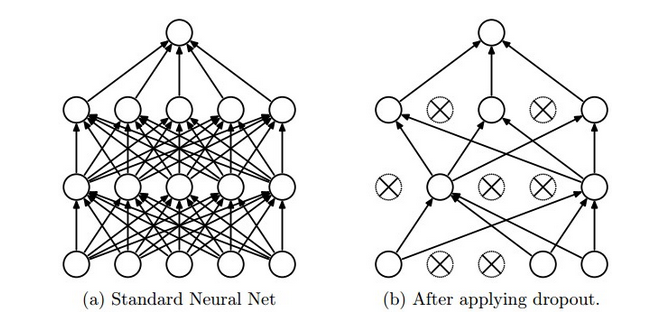
- Training: Dropout can be interpreted as sampling a Neural Network within the full Neural Network
- Testing: not applied
Batch Normalization¶
- Bad Weight Initialization
- Vanishing Gradients
- Normalize data right before non-linearities (or after ?!)

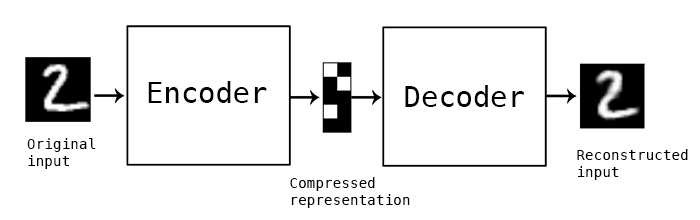
Autoencoders¶
- Autoencoders tries to recover input signal from compressed representation
- so they should save only the most valuable inforation!
- dimention reduction!
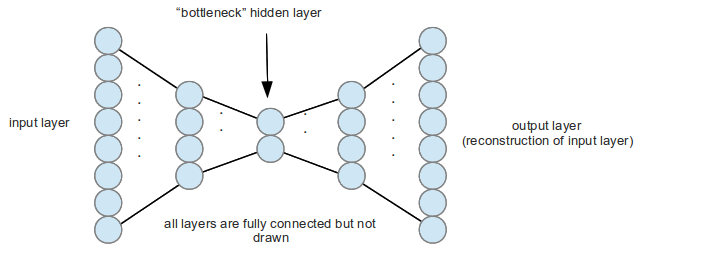
Autoencoders¶
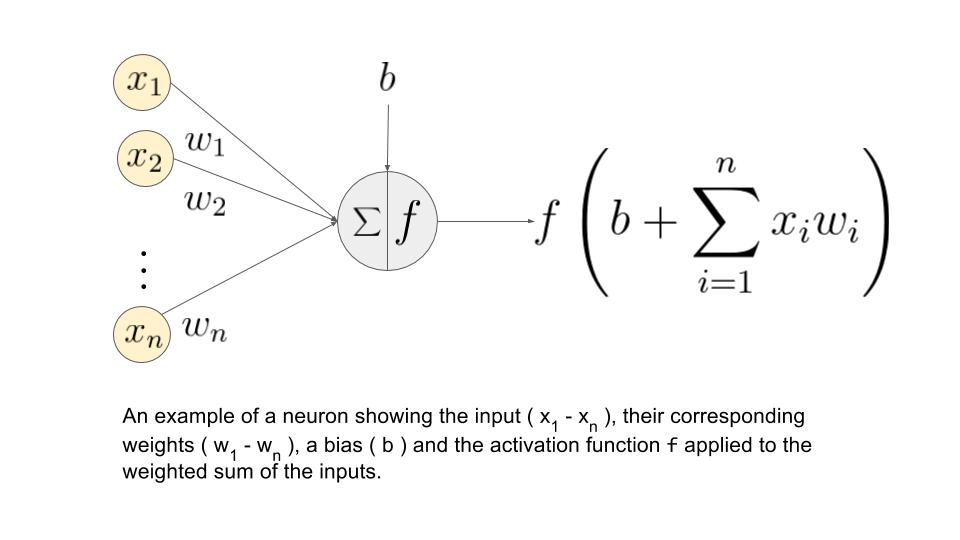

 >
>