Data Analysis
Andrey Shestakov (avshestakov@hse.ru)
Clustering1
1. Some materials are taken from machine learning course of Victor Kitov
Clustering¶
Aim of clustering¶
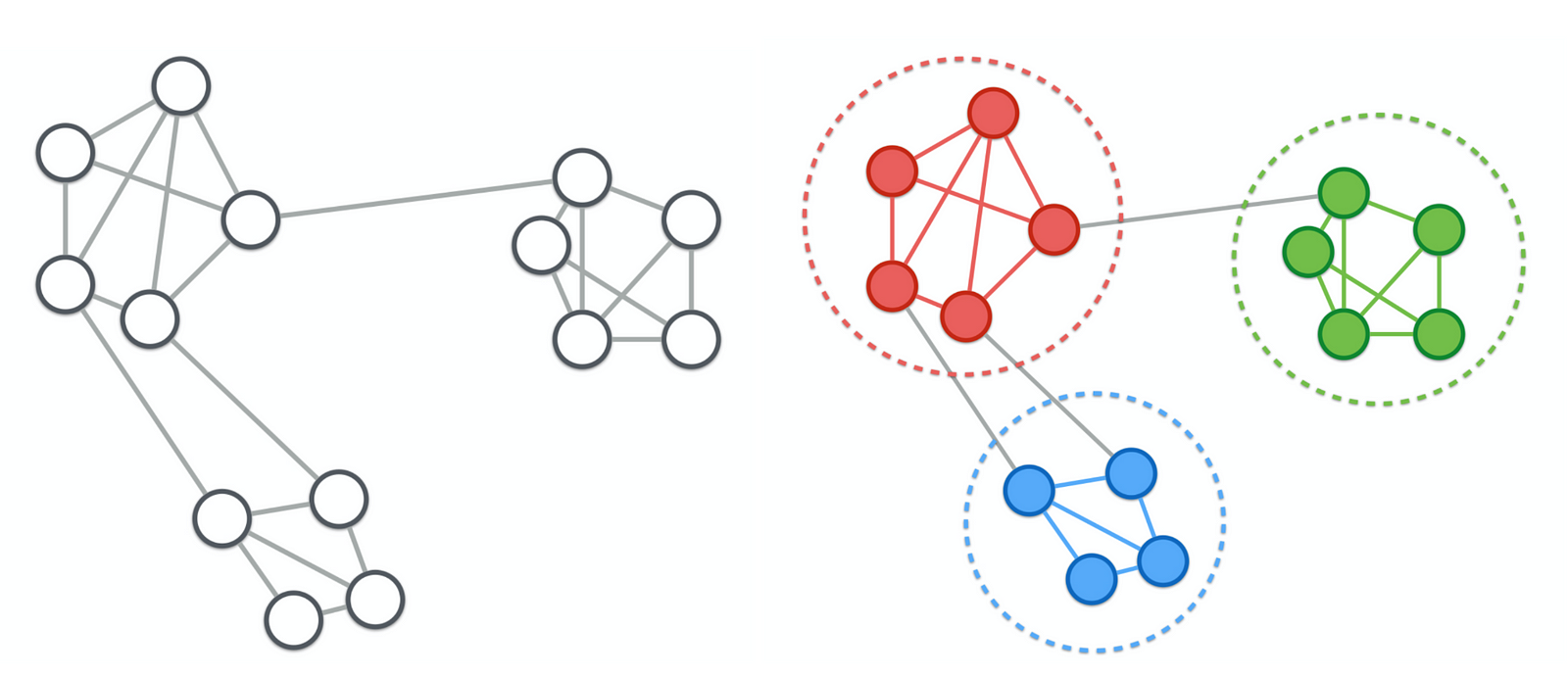
Clustering is partitioning of objects into groups so that:
- inside groups objects are very similar
- objects from different groups are dissimilar
Aim of clustering¶
- Unsupervised learning
- No definition of ''similar''
- different algorithms use different formalizations of similarity
Applications of clustering¶
- data summarization
- feature vector is replaced by cluster number
- feature extraction
- cluster number, cluster average target, distance to native cluster center / other clusters
- community detection in networks
- nodes - people, similarity - number of connections
- outlier detection
- outliers do not belong any cluster
Groups of clustering methods¶
- Prototype-based
- Replace cluster with ethalon object
- Hierarchcal
- Build cluster hierarchy
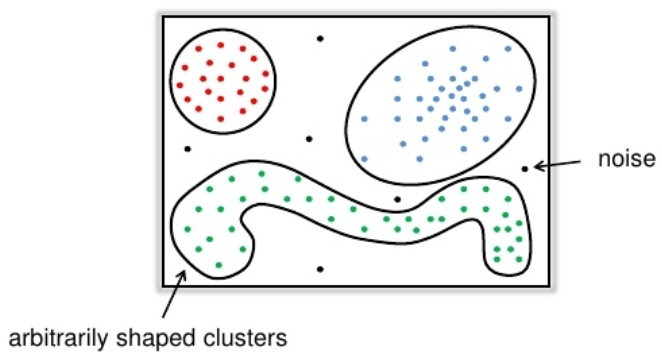
- Density-based
- Find dence groups of objects
- Spectral
- Use spectral techniques
- Grid-based
- Split feature space in grids and connect them
- Probabilistic models
- Assume some mixture of probability distributions
Clustering algorithms comparison¶
We can compare clustering algorithms in terms of:
- computational complexity
- do they build flat or hierarchical clustering?
- can the shape of clustering be arbitrary?
- if not is it symmetrical, can clusters be of different size?
- can clusters vary in density of contained objects?
- robustness to outliers
Prototype-based clustering¶
- Clustering is flat (not hierarchical)
- Number of clusters $K$ is specified in advance
- Each object $x_{n}$ is associated with a cluster $z_{n}$
- $z_{n} \in \{1,\dots,K\}$
- Each cluster $C_{k}$ is defined by its representative $\mu_{k}$, $k=1,2,...K.$
- Criterion to find representatives $\mu_{1},...\mu_{K}$: $$ Q(z_{1},...z_{N})=\sum_{n=1}^{N}\min_{k}\rho(x_{n},\mu_{k})\to\min_{\mu_{1},...\mu_{K}} $$
Generic algorithm¶

Comments¶
different distance functions lead to different algorithms:
- $\rho(x,x')=\left\lVert x-x'\right\rVert _{2}^{2}$=> K-means
- $\rho(x,x')=\left\lVert x-x'\right\rVert _{1}$=> K-medians
$\mu_{k}$ may be arbitrary or constrained to be existing objects
$K$ - is set by user
- if chosen small=>distinct clusters will get merged
- better to take $K$ larger and then merge similar clusters.
Shape of clusters is defined by $\rho(\cdot,\cdot)$
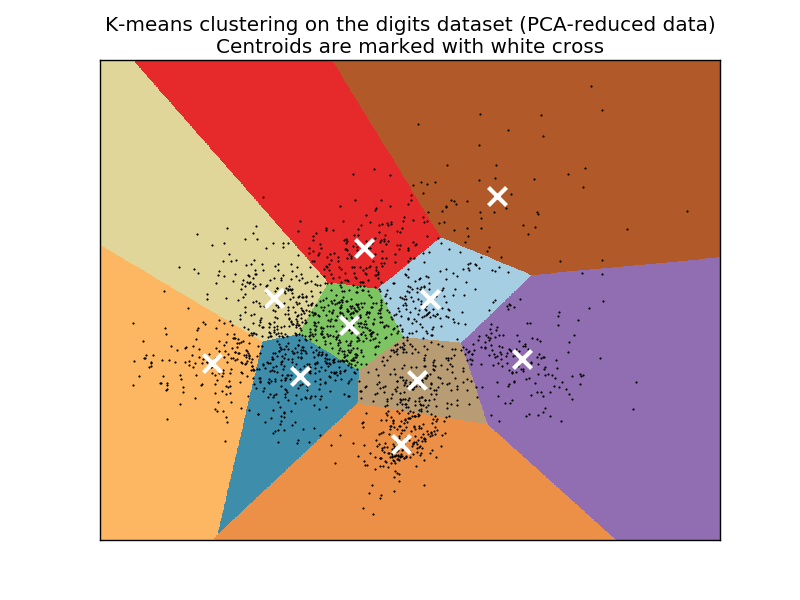
Example¶

K-means algorithm¶
- Suppose we want to cluster our data into $K$ clusters.
- Cluster $i$ has a center $\mu_{i}$, i=1,2,...K.
- Consider the task of minimizing $$ \sum_{n=1}^{N}\left\lVert x_{n}-\mu_{z_{n}}\right\rVert _{2}^{2}\to\min_{z_{1},...z_{N},\mu_{1},...\mu_{K}}\quad (1) $$ where $z_{i}\in\{1,2,...K\}$ is cluster assignment for $x_{i}$ and $\mu_{1},...\mu_{K}$ are cluster centers.
- Direct optimization requires full search and is impractical.
- K-means is a suboptimal algorithm for optimizing (1).
K-means algorithm¶

K-means properties¶
- Convergence conditions
- maximum number of iterations reached
- cluster assignments $z_{1},...z_{N}$ stop to change (exact)
- $\{\mu_{i}\}_{i=1}^{K}$ stop changing significantly (approximate)
- Initialization:
- typically $\{\mu_{i}\}_{i=1}^{K}$ are initialized to randomly chosen training objects
K-means properties¶
- Optimality:
- criteria is non-convex
- solution depends on starting conditions
- may restart several times from different initializations and select solution giving minimal value of (1).
- Complexity: $O(NDKI)$
- $K$ is the number of clusters
- $I$ is the number of iterations.
- usually few iterations are enough for convergence.
Gotchas¶
- K-means assumes that clusters are convex:
- It always finds clusters even if none actually exist
- need to control cluster quality metrics
Main factors of solution¶
- Initial position of centroids
- Number of centroids
Number of centroids - K¶
- Don't use vanilla k-means (X-means, ik-means)
- Consider cluster quality measures
- Use heuristics
Elbow method¶
- Criterion of k-means $$ Q(C) = Q(z_{1},...z_{N}) = \sum_{n=1}^{N}\left\lVert x_{n}-\mu_{z_{n}}\right\rVert _{2}^{2}\to\min_{z_{1},...z_{N},\mu_{1},...\mu_{K}}\quad (1) $$
- Lets take all possible values of $K$, and chose one that delivers minimum of $Q(C)$!
- Won't work! Why?
Elbow method¶
- Choose $K$ after which $Q(C)$ stops decreasing rapidly
- A bit more formally $$ D(k) = \frac{|Q^{(k)}(C) - Q^{(k+1)}(C)|}{|Q^{(k-1)}(C) - Q^{(k)}(C)|} \quad \text{" is small "} $$
In [13]:
plot = interact(elbow_demo, k=IntSlider(min=2,max=8,step=1,value=2))
Warning!¶
- Heuristics are not dogma!
- If at least some clusters are interpretable - this is good
Centroid initialization¶
- Initiallize randombly
- Run multiple times and take result with smallest $Q(C)$
- Use result of another clustering method as starting point
- k-means++
K-means++¶
- Choose 1st centroid randomly from initial objects
- For each data point calculate its distance to closest centroid $d_{\min}(x_i) = \min_{\mu_j} \|x_i - \mu_j\|^2$
- Take point as next centroid with probability $p(x_i) \propto d_{\min}(x_i)$
In [15]:
interact(demo_kmpp, iters=IntSlider(min=1,max=6,step=1,value=1))
Out[15]:
<function __main__.demo_kmpp>
K-means¶
- Not robust to outliers
- K-medians is a bit more robust
- K-representatives may create singleton clusters in outliers if centroids get initialized with outlier
- better to init centroids with mean of $m$ randomly chosen objects
- Constructs spherical clusters of similar radii
- Allows kernel version which can find non-convex clusters in original space
Hierarchical clustering¶
Insparation - Motivation¶
Insparation - Motivation¶
- Number of clusters $K$ not known a priory.
- Clustering is usually not flat, but hierarchical with different levels of granularity:
- sites in the Internet
- books in library
- animals in nature
Hierarchical clustering¶
Hierarchical clustering may be:
- top-down
- divisive clustering
- bottom-up
- aglomerative clustering
Aglomerative example¶
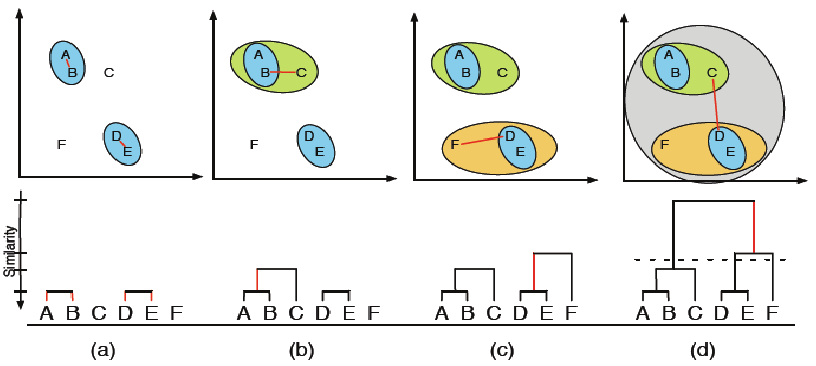
Dendrogram¶
Algorithm¶

- What is "closest pair of clusters"?
- How do we recalculate distances between clusters?
Distance recalculation¶
- Consider clusters $A=\{x_{i_{1}},x_{i_{2}},...\}$ and $B=\{x_{j_{1}},x_{j_{2}},...\}$.
- We can define the following natural ways to recalculate distances
- nearest neighbour (or single link) $$ \rho(A,B)=\min_{a\in A,b\in B}\rho(a,b) $$
- furthest neighbour (or complete link) $$ \rho(A,B)=\max_{a\in A,b\in B}\rho(a,b) $$
- group average link $$ \rho(A,B)=\frac{1}{N_AN_B}\sum\limits_{a\in A,b\in B}\rho(a,b) $$
- closest centroid (or centroid-link) $$ \rho(A,B)=\rho(\mu_{A},\mu_{B}) $$ where $\mu_{U}=\frac{1}{|U|}\sum_{x\in U}x$ or $m_{U}=median_{x\in U}\{x\}$
Lance–Williams formula¶
$$ \rho(C_i \cup C_j, C_k) = a_i \cdot \rho(C_i, C_k) + a_j \cdot \rho(C_j, C_k) + b \cdot \rho(C_i, C_j) + c \cdot |\rho(C_i, C_k) - \rho(C_j, C_k)|$$
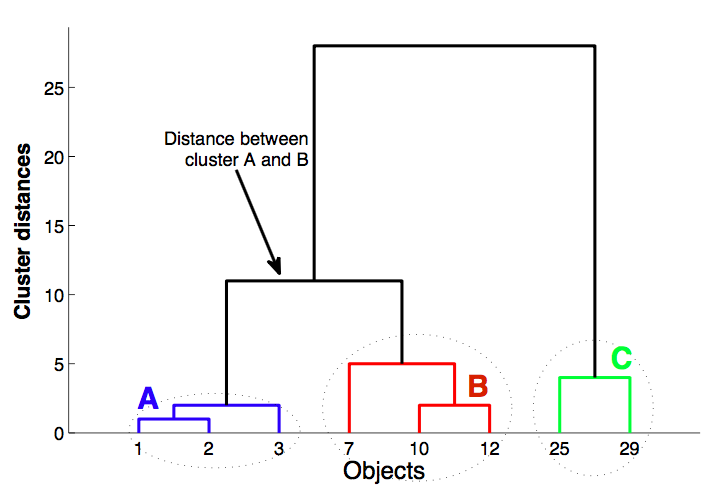
Heuristics for dendrogram quality¶
- cophenetic distance between objects $x_i$ и $x_j$ - height of dendrogram at which whose two objects have merged
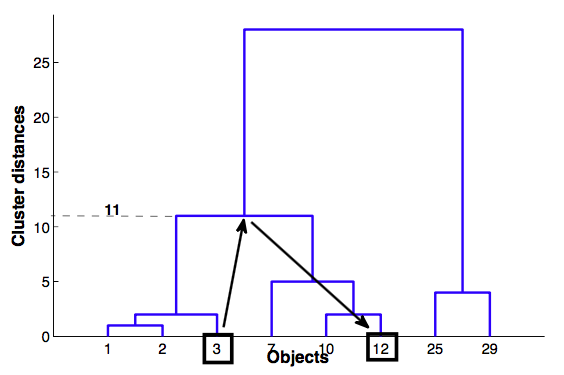
Cophenetic correlation¶
- Cophenetic correlation — correlation between Cophenetic distance and simple distance between objects
If dendrogram is good, correlation should be high
In [17]:
interact(coph_demo, k=IntSlider(min=2, max=10, step=1, value=2), link=['complete', 'single', 'average', 'centroid'], metric=['euclidean', 'cityblock'])
Out[17]:
<function __main__.coph_demo>
Comments¶
- Results in full hierarchy of objects
- Various ways to calculate distances
- Nice visualization
- Needs a lot of resources
Idea¶
- Identify 2 parameters
- $\epsilon$ - radius of neighbourhood of each point. $N_\epsilon(p)$ - neighbourhood of point $p$
min_pts- minimal number of points inside neighbourhood
- To start a cluster from point there should be at least
min_ptspoints in $N_\epsilon$ - If this conditions is satisfied - spread cluster and check all points neighbours by the same crierion
Types of points¶
- Core point: point having $\ge \texttt{min_pts}$ points in its $\varepsilon$ neighbourhood
- Border point: not core point, having at least 1 core point in its $\varepsilon$ neighbourhood
- Noise point: neither a core point nor a border point
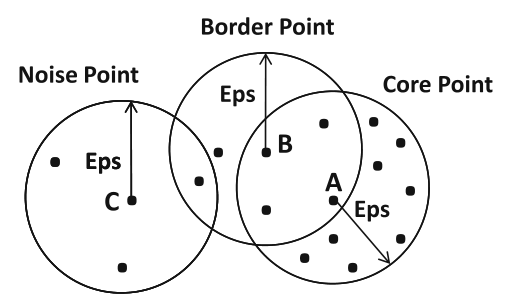
DBSCAN¶
{C}
1.function dbscan(X, eps, min_pts):
2. initialize NV = X # not visited objects
3. for x in NV:
4. remove(NV, x) # mark as visited
5. nbr = neighbours(x, eps) # set of neighbours
6. if nbr.size < min_pts:
7. mark_as_noise(x)
8. else:
9. C = new_cluster()
10. expand_cluster(x, nbr, C, eps, min_pts, NV)
11. yield Cexpand_cluster¶
{C}
1. function expand_cluster(x, nbr, C, eps, min_pts, NV):
2. add(x, C)
3. for x1 in nbr:
4. if x1 in NV: # object not visited
5. remove(NV, x1) # mark as visited
6. nbr1 = neighbours(x1, eps)
7. if nbr1.size >= min_pts:
8. # join sets of neighbours
9. merge(nbr, nbr_1)
10. if x1 not in any cluster:
11. add(x1, C)In [19]:
interact(dbscan_demo, eps=FloatSlider(min=0.1, max=10, step=0.05, value=1), min_pts=IntSlider(min=2, max=15, step=1, value=5))
Out[19]:
<function __main__.dbscan_demo>
Recap¶
- Do not indicate number of clusters
- Arbitrary shapes of clusters
- Identifies outliers
- Problems with varying density
Failure for varying density¶
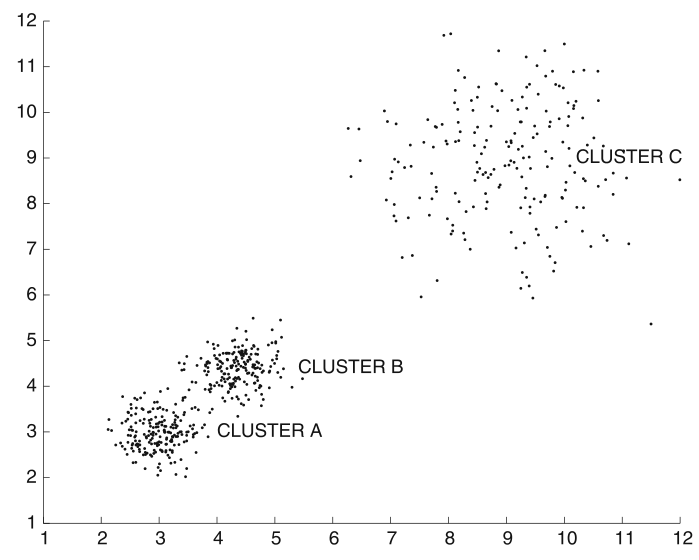
- Large
min_pts: cluster C is missed - Small
min_pts: clusters A and B get merged
Cluster Validity and Quality Measures¶
General approaches¶
- Evaluate using "ground-truth" clustering (Quality Measure)
- invariant to cluster naming
- Unsupervised criterion (Cluster Validity)
- based on intuition:
- objects from same cluster should be similar
- objects from different clusters should be different
- based on intuition:
Based on ground-truth¶
Rand Index¶
$$ \text{Rand}(\hat{\pi},\pi^*) = \frac{a + d}{a + b + c + d} \text{,}$$where
- $a$ - number of pairs that are grouped both in $\hat{\pi}$ and
- $d$ - number of pairs that are separated both in $\hat{\pi}$ and $\pi^*$ $\pi^*$,
- $b$ ($c$) - number of pairs that are separated both in $\hat{\pi}$ ($\pi^*$), but grouped in $\pi^*$ ($\hat{\pi}$)
Rand Index¶
$$ \text{Rand}(\hat{\pi},\pi^*) = \frac{tp + tn}{tp + fp + fn + tn} \text{,}$$where
- $tp$ - number of pairs that are grouped both in $\hat{\pi}$ and
- $tn$ - number of pairs that are separated both in $\hat{\pi}$ and $\pi^*$ $\pi^*$,
- $fp$ ($fn$) - number of pairs that are separated both in $\hat{\pi}$ ($\pi^*$), but grouped in $\pi^*$ ($\hat{\pi}$)
Adjusted Rand Index
$$\text{ARI}(\hat{\pi},\pi^*) = \frac{\text{Rand}(\hat{\pi},\pi^*) - \text{Expected}}{\text{Max} - \text{Expected}}$$Precision, Recall, F-measure¶
- $\text{Precision}(\hat{\pi},\pi^*) = \frac{tp}{tp+fn}$
- $\text{Recall}(\hat{\pi},\pi^*) = \frac{tp}{tp+fp}$
- $\text{F-measure}(\hat{\pi},\pi^*) = \frac{2\cdot Precision \cdot Recall}{Precision + Recall}$
Cluster validity¶
- Intuition
- objects from same cluster should be similar
- objects from different clusters should be different
Silhouette¶
For each object $x_{i}$ define:
- $s_{i}$-mean distance to objects in the same cluster
- $d_{i}$-mean distance to objects in the next nearest cluster Silhouette coefficient for $x_{i}$: $$ Silhouette_{i}=\frac{d_{i}-s_{i}}{\max\{d_{i},s_{i}\}} $$
Silhouette coefficient for $x_{1},...x_{N}$: $$ Silhouette=\frac{1}{N}\sum_{i=1}^{N}\frac{d_{i}-s_{i}}{\max\{d_{i},s_{i}\}} $$
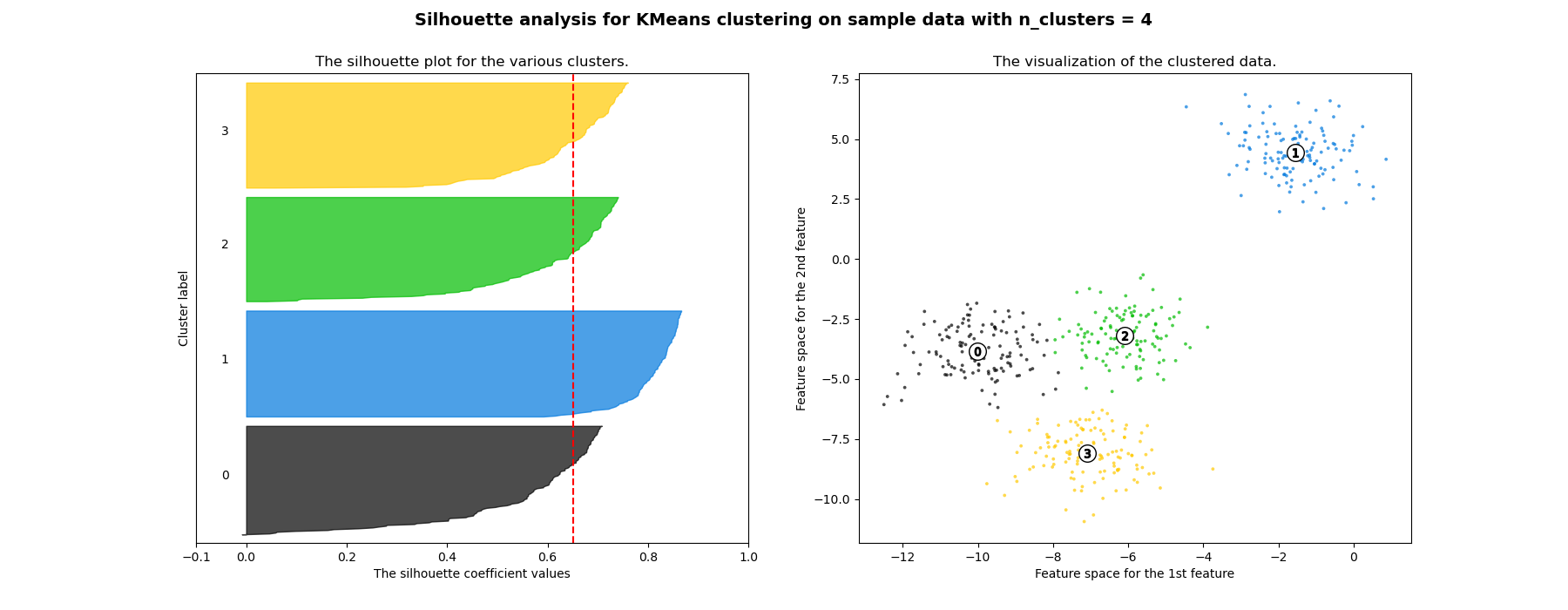
Discussion¶
Advantages
- The score is bounded between -1 for incorrect clustering and +1 for highly dense clustering.
- Scores around zero indicate overlapping clusters.
- The score is higher when clusters are dense and well separated.
Disadvantages
- complexity $O(N^{2}D)$
- favours convex clusters
What else?¶
- Mixture Models (maybe next)
- Spectral clustering
- Community Detection
- Consensus clustering!