
Data Analysis
Andrey Shestakov (avshestakov@hse.ru)
Introduction to Recommender Systems1
1. Some materials are taken from machine learning course of Victor Kitov
Motivation¶
Everyday people have to make decisions:
- what music to listen
- what movies to see
- what books to read
- what food to eat
- what games to play
- ...
Multitude of choices
- Spotify - 30kk. songs
- Netflix - 20k. movies and series
- Amazon - 500k. books
- Steam - 20k games
To filter out the seach people can rely on recommendations
- of their friends (if there are friends)
- of some reviews
These recommendations are too narrow and standard
- rely on information of a handful of people
- not tuned for individual user tastes
Need automatic recommendation system!

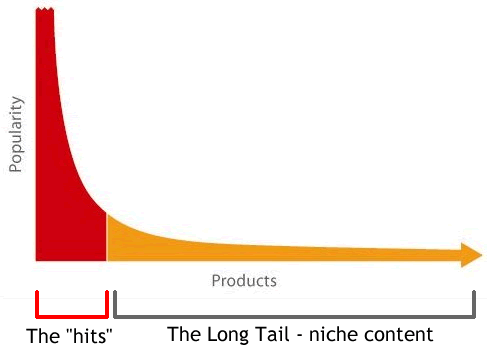
Long Tail Phenomenon¶

Few words on history¶
Netflix prize¶
- Competition for the best recommendation algirithm
- October 2007 - September 2009
- Prize: 1 000 000 $
- 480 000 users
- 17 770 movies
- format: [user, movie, datetime, rating]
- grades: 1,2,3,4,5
- quality measure: RMSE
Netflix Prize¶

Collaborative filtering¶
Collaborative filtering¶
A method of making automatic predictions about the interests of a user by collecting prefences or taste information from similar users
- Generic CF algorithm
- Look for users who share the same rating patterns with current user
- Use their ratings to predict currently unknown user ratings
- Main assumption: if person A has the same opinion as a persion B on an issue, A is more likely to have B's opinion on a different issue.
- Have you already seen this idea?
Collaborative filtering¶
Challenges¶
- Scalability
- many users and items
- Cold start
- new user has not rated many items - hard to predict his preferences
- new item was not rated by many users - hard to predict its characteristics
- Shilling attacks
- shop representatives may give lots of positive ratings for their own items ang negative ratings for theis competitors
- Learning Loop
- once the model have been relearned it may relearned its previous predictions - does not gain new knowledge
- Obvious recommendations
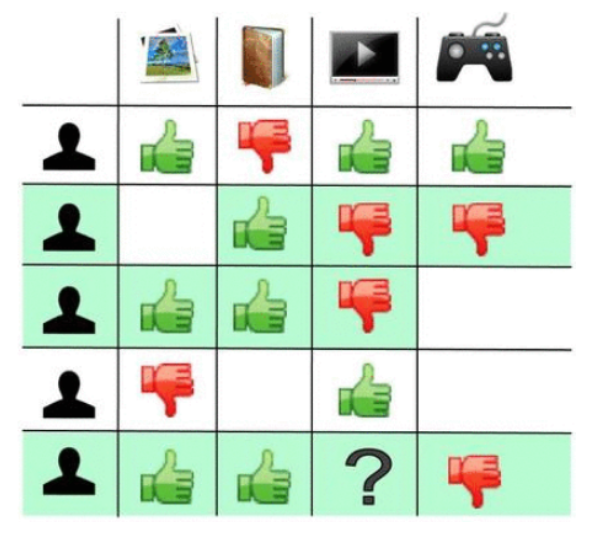
Core concepts¶
- Users give ratings to items

- Users give ratings to items
- Binary
- "Stars"
- Implicit
- Tasks of RecSys:
- Fill missing values of the ratings
- Recommend items to user
- may not be the highest ranked!
Notations¶
- $U$ - set of all users
- $I$ - set of all items
- $u$, $v$ - some users
- $i$, $j$ - some items
- $U_i$ - set of users, that rated item $i$
- $I_u$ - set of items, that have been rated by user $u$
- $R_{ui}$ - actual rating of item $i$ by user $u$
- $\hat{R}_{ui}$ - predicted rating of item $i$ by user $u$
Baseline¶
Baseline ideas¶
- $b_{ui} = \mu$, $(\mu = \frac{1}{n}\sum\limits_{u,i} R_{ui})$
- $b_{ui} = \bar{R}_u = \frac{1}{|I_u|}\sum\limits_{i\in I_u} R_{ui}$
- $b_{ui} = \bar{R}_i = \frac{1}{|U_i|}\sum\limits_{u\in U_i} R_{ui}$
General baseline¶
- $b_{ui} = \mu + b_u + b_i$,
- $b_{u} = \frac{1}{|I_u|}\sum_{i\in I_u}(R_{ui} - \mu)$
- $b_{i} = \frac{1}{|U_i|}\sum_{u\in U_i}(R_{ui} - b_u - \mu)$
Intuition
- $b_u$ is how much higher user rates items than on average
- $b_i$ is how much item $i$ is rated higher than average user rating
General baseline¶
- $b_{ui} = \mu + b_u + b_i$,
- $b_{u} = \frac{1}{|I_u|+\alpha}\sum_{i\in I_u}(R_{ui} - \mu)$
- $b_{i} = \frac{1}{|U_i|+\beta}\sum_{u\in U_i}(R_{ui} - b_u - \mu)$
- What is the idea behind $\alpha$ and $\beta$?
Motivation¶
- Compare accuracy with advanced model
- Can compute missing values with baseline values
- Normalization: predict $R_{ui} - b_{ui}$ instead of $R_{ui}$
User-based Collaborative filteting¶
User-based CF¶
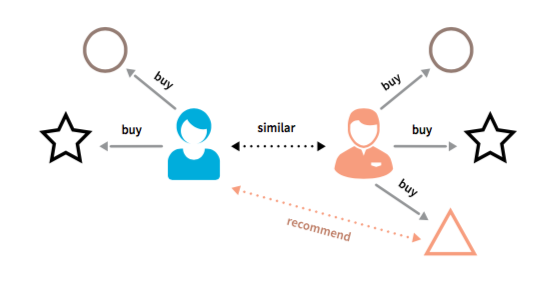
User-based CF¶
- Also known as K-NN CF
Define similarity function on users: $s \in \mathbb{R}^{U \times U}$
Algorithm with level normalization:
- For user $u$ find a neighbourhood of similar users $N(u)$
- Generate rating predictions by averaging over $N(u)$ $$ \hat{R}_{ui} = \bar{R}_u + \frac{\sum_{v \in N(u)} s_{uv}(R_{vi} - \bar{R}_v)}{\sum_{v \in N(u)} \left| s_{uv}\right|} $$
$\bar{R}_u$ - adjustment to compensate average rating behaviour of u
- skeptics/optimists normalization
User-based CF¶
Algorithm with level and scale normalization:
- For user $u$ find a neighbourhood of similar users $N(u)$
- Generate rating predictions by averaging over $N(u)$ $$ \hat{R}_{ui} = \bar{R}_u + \sigma_u\frac{\sum_{v \in N(u)} s_{uv}(R_{vi} - \bar{R}_v)/\sigma_v}{\sum_{v \in N(u)} \left| s_{uv}\right|} $$
where $\sigma_u$ is standard deviation of user $u$ ratings
Number of NN¶
- In general 20-50 is suggested
- Also possible
- Take all
- Top-k
- $s_{uv} > \theta$
Similarity measures¶
For each pair $(u,v)$ the intersection of rated items should be considered!
Pearson correlation $$ s_{uv} = \frac{\sum\limits_{i \in I_u\cap I_v} (R_{ui} - \bar{R}_u)(R_{vi} - \bar{R}_v)}{\sqrt{\sum\limits_{i \in I_u\cap I_v}(R_{ui} - \bar{R}_u)^2}\sqrt{\sum\limits_{i \in I_u\cap I_v}(R_{vi} - \bar{R}_v)^2}}$$
tends to give high similarity for users with few ratings
- solution $s'_{uv} = s_{uv}\cdot \min\{|I_u\cap I_v|/50, 1\}$
Other possible measures¶
- Spearman correlation
- correlatino between ranks of ratings
- captures the level of monotone dependencies
- Cosine similarity $$ s_{uv} = \frac{\sum\limits_{i \in I_u\cap I_v} R_{ui} R_{vi}}{\sqrt{{\sum\limits_{i \in I_u\cap I_v}R_{ui}^2}}\sqrt{{\sum\limits_{i \in I_u\cap I_v}R_{vi}^2}}}$$
Item-based Collaborative filteting¶
Item-based CF¶

Item-based CF¶
- Also determine similarity function between items $s \in \mathbb{R}^{I \times I}$
For item $i$ find a set of items similar to it and rated by user $u$: $N(i)$
Predict $R_{ui}$ by averaging over $N(i)$ $$ \hat{R}_{ui} = \frac{\sum_{j \in N(i)} s_{ij}R_{uj}}{\sum_{j \in N(i)} \left| s_{ij}\right|} \qquad (1)$$
Similarities for Item-based CF¶
- Conditional probability of purchase $$ s_{ij} = \frac{n_{ij}}{n_i} $$
- Dependency $$ s_{ij} = \frac{n_{ij}}{n_i n_j} $$
Benefits of item-based CF¶
- We need to generate recomendations for user $u$ in real-time when he is active
When user is active - his ratings change
- User-based CF: after changes in rating we need to recalculate all nearest neighbours or user - long!
- Item-based CF: for each pair of items we precalculate similarities $s_{ij}$ and find nearest neighbours of each item. Change in user ratings affects only the weights in $(1)$
Due to possible precomputations, item-item becomes more efficient
- user profile is more dynamic
- item profile is more static
Latent variable models¶
Latent variables models¶
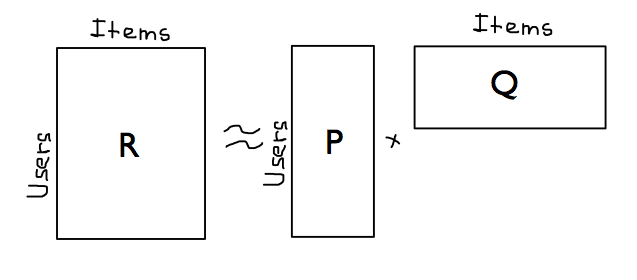
For each user $u$ build a vector $p_u\in \mathbb{R}^{k}$ and for each item $i$ - a vector $q_i \in \mathbb{R}^{k}$ s.t.: $$ R_{ui} \approx p_u^\top q_i $$
- $p_u$'s components sometimes can be iterpreted as user's interests in topic
- $q_i$'s components sometimes can be iterpreted as items's relevance to topic
Singular Value Decomposition¶
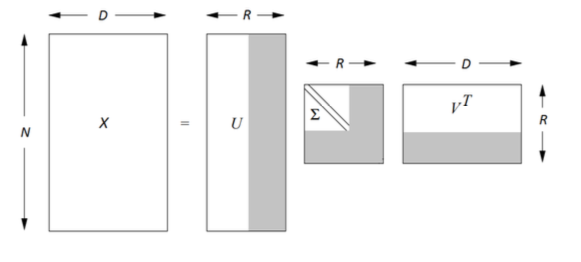
Each matrix $X\in \mathbb{R}^{n \times d}$ with rank $r$ can be decomposed as $$ X = U \Sigma V^\top ,$$ where
- $U$ - unitary matrix, which contains eigenvectors of $XX^\top$
- $V$ - unitary matrix, which contains eigenvectors of $X^\top X$
- $\Sigma$ - diagonal matrix with singular values $\sigma_i = \sqrt{\lambda_i}$
Truncated SVD¶
Truncated SVD with rank $K$ $$ X \approx \hat{X} = U_k \Sigma_k V_k^\top ,$$ where
- $U_k$ contains first $k$ columns of $U$
- $V_k$ contains first $k$ columns of $V$
- $\Sigma_k$ contains first $k$ diagonal elements of $\Sigma$
SVD разложение¶
It turns out that $$ \hat{X} = \arg \min\limits_{A\in \mathbb{R}{n \times d}, rank(A) \leq k} \| X-A \|_{Frobenius} $$
Problems¶
- Have to fill missing values
- with $0$
- with baseline predictions
- Optionally
- $R' = R-B$ and fill with $0$
- In the end:
- $P = U \Sigma^{1/2}$
- $Q = \Sigma^{1/2}V^\top$
- $\hat{R} = P^\top Q$
- How do we calculate $p_u$ for new user $u$ given his rating vector $r_u$?
Recalculation for new user¶
$$ p_u = \arg \min\limits_p \|r_u - Vp \|^2 = \{\text{OLS solution}\} = \left( V^\top V \right)^{-1} V^\top r_u = V^\top r_u$$- $p_u = V^\top r_u$ is a vector of scalar products $[\langle v_1, r_u \rangle, \langle v_2, r_u \rangle, \dots, \langle v_k, r_u \rangle]$
- Backward transformation from low-dimensional representation $p_u$ to initial representation $\hat{r}_u$: $\hat{r}_u = Vp_u$
Latent Factor Model (Sparse SVD)¶
- Lets optimize $$ \sum\limits_{u,i}(R_{ui} - \bar{R}_u - \bar{R}_i - \langle p_u, q_i \rangle)^2 \rightarrow \min\limits_{P, Q} $$
- Using SGD and going through pairs $(u,i)$ with known $R_{ui}$: $$ p_{uk} = p_{uk} + 2\alpha \left(q_{ik}(R_{ui} - \bar{R}_u - \bar{R}_i - \langle p_u, q_i \rangle\right)$$ $$ q_{ik} = q_{ik} + 2\alpha \left(p_{uk}(R_{ui} - \bar{R}_u - \bar{R}_i - \langle p_u, q_i \rangle\right)$$
Latent Factor Model (Sparse SVD)¶
- Add regularization $$ \sum\limits_{u,i}(R_{ui} - \bar{R}_u - \bar{R}_i - \langle p_u, q_i \rangle)^2 + \lambda \sum_u\| p_u \|^2 + \mu\sum_i\| q_i \|^2 \rightarrow \min\limits_{P, Q} $$
- Using SGD and going through pairs $(u,i)$ with known $R_{ui}$: $$ p_{uk} = p_{uk} + 2\alpha \left(q_{ik}(R_{ui} - \bar{R}_u - \bar{R}_i - \langle p_u, q_i \rangle) - \lambda p_{uk}\right)$$ $$ q_{ik} = q_{ik} + 2\alpha \left(p_{uk}(R_{ui} - \bar{R}_u - \bar{R}_i - \langle p_u, q_i \rangle) - \mu q_{ik}\right)$$
Factorization Machines¶
- Represent all users and items iteractions with one-hot encoded vector (of length $d=|U|+|I|$):
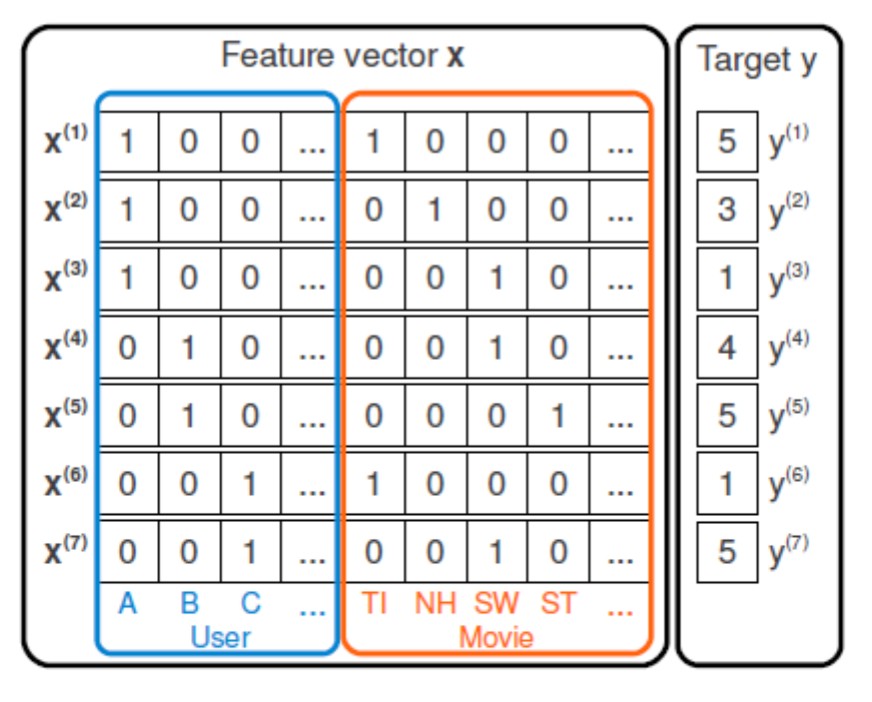
- In such feature space we can consider various models:
Factorization Machines¶

- Let's try to reduce the number of parameters and approximate $w_{ij}$ with $\langle v_i, v_j\rangle$, where $v_i$ is latent representation of feature $x_j$
Factorization Machines¶
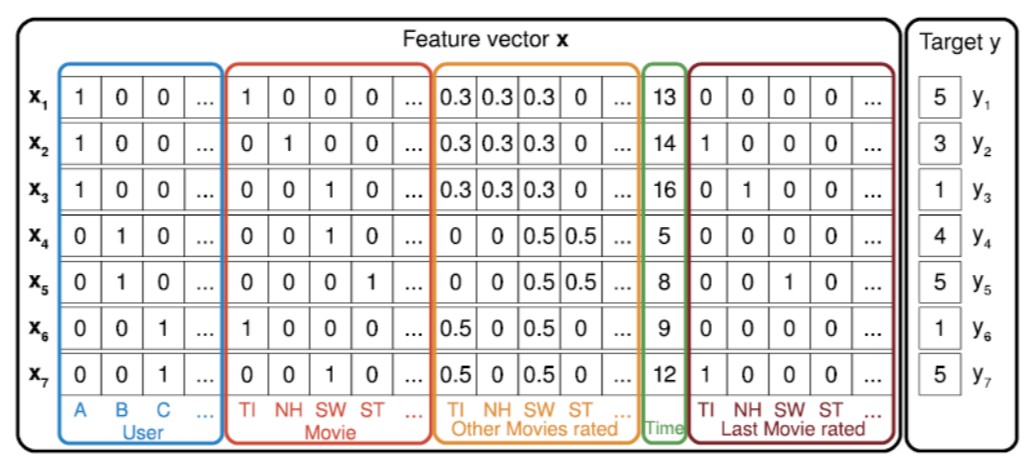
Classification-based models¶
- How can we adapt simple classification task to recommendation system domain?
- Any problems here?
Measuring Quality¶
- Ratings accuracy
- MAE, MSE
- Event quality
- F-score, ROC-AUC, PR-AUC
- precision@k, recall@k
- Ranking quality
- $DCG@k(u) = \sum\limits_{p=1}^k \frac{rel(i,p)}{\log{(p+1)}}$
- $nDCG@k(u) = \frac{DCG@k(u)}{\max{(DCG@k(u))}}$
- What else is usefull to measure?
