
Data Analysis
Andrey Shestakov (avshestakov@hse.ru)
Support Vector Machine. Kernel Trick1
1. Some materials are taken from machine learning course of Victor Kitov
Let's recall previous lecture¶
- Various quality measures for regression and classification
- Like...
Aaand linear classification¶
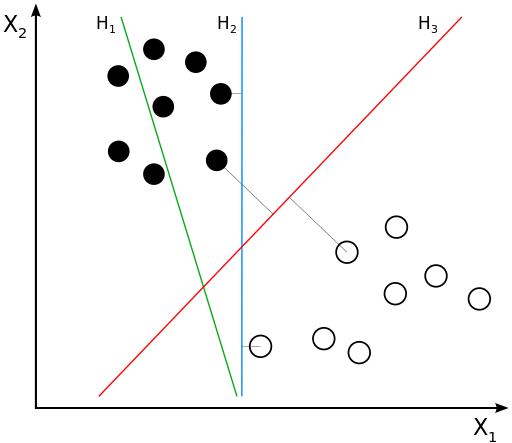
General idea of SVM: select hyperplane that maximizes the spread between classes
Linearly separable case¶
Recap of linear classification¶
Discriminant function $$g(x) = w_0 + w_1x_1 + w_2x_2 = w_0 + \langle w, x \rangle = w_0 + w^\top x $$
- If $g(x^*) > 0$, then $y^* = \text{'black'} = +1$
- If $g(x^*) < 0$, then $y^* = \text{'white'} = -1$
- $\frac{|g(x)|}{||w||}$ - distance from point $x$ to hyperplane
Problem statement¶
- For all objects:
- $w_0 + \langle w, x_i \rangle \geq b$, if $y_i = + 1$
- $w_0 + \langle w, x_i \rangle \leq - b$, if $y_i = - 1$
- Notice, that $g(x) = w_0 + \langle w, x \rangle$ and $g'(x) = c \cdot (w_0 + \langle w, x \rangle)$, $\forall c>0$ describe the same hyperplane
- Lets set $c$ such that $\min\limits_i M_i = \min\limits_i y \cdot g(x_i) = 1$
- That means that:
- $w_0 + \langle w, x_i \rangle \geq 1$, if $y_i = + 1$
- $w_0 + \langle w, x_i \rangle \leq - 1$, if $y_i = - 1$
Problem statement¶

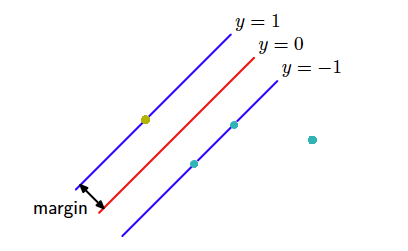
- "Street" between classes: $ -1 \leq w_0 + \langle w, x \rangle \leq +1$
- "Street" width: $$\langle (x_{+} - x_{-}) , \frac{w}{||w||}\rangle = \frac{\langle w, x_{+} \rangle - \langle w, x_{-} \rangle }{||w||} = \frac{2}{||w||} \rightarrow \max$$
- Problem statement: $$ \begin{cases} \frac{1}{2} ||w||^2 \rightarrow \min \\ y_i(\langle w, x_i \rangle + w_0 ) \geq 1 \quad i=1\dots n \end{cases} $$
Problem statement: dual problem¶
- Initial statement: $$ \begin{cases} \frac{1}{2} ||w||^2 \rightarrow \min \\ y_i(\langle w, x_i \rangle + w_0 ) \geq 1 \quad i=1\dots n \end{cases} $$
By Karush-Kuhn-Takker:
$$\begin{cases} \mathcal{L}(w,w_0,\lambda) = \frac{1}{2} ||w||^2 - \sum\limits_i \lambda_i \left( y_i(\langle w, x \rangle + w_0 ) - 1\right) \rightarrow \min\limits_{w,w_0}\max\limits_{\lambda} \\ \lambda_i \geq 0 \quad i=1\dots n\\ \lambda_i = 0 \text{, or } y_{i}(\langle w, x_i \rangle + w_0)=1 \quad i=1\dots n \end{cases}$$Support vectors¶
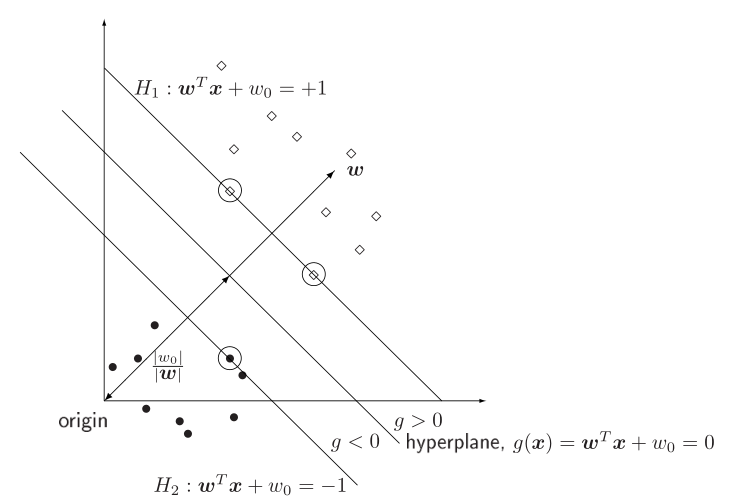
non-informative observations: $y_{i}(\langle w, x_i \rangle + w_0)>1$ (or $\lambda_i = 0$)
- do not affect the solution
support vectors: $y_{i}(x_{i}^{T}w+w_{0})=1$ (or $\lambda_i > 0$)
- lie at distance $1/\|w\|$ to separating hyperplane
- affect the the solution.
Problem statement: dual problem¶
Necessary condition:
- $\frac{\partial \mathcal{L} }{\partial w} = w - \sum\limits_i \lambda_iy_ix_i = 0 \quad \Rightarrow \quad w = \sum\limits_i \lambda_iy_ix_i$
- $\frac{\partial \mathcal{L} }{\partial w_0} = \sum\limits_i \lambda_iy_i = 0$
- Depends on dot product of features, not features themselves
- $\mathcal{L}(\lambda)$ - convex
- Have a unique solution
- Once $\lambda_i$ are found: $w = \sum\limits_i \lambda_iy_ix_i$
- $w_0$ can be found as mean or median of $\{\langle w, x_i \rangle - y_i: \lambda_i \neq 0\}$
interact(lin_sep_svm_demo, class_sep=FloatSlider(min=0.4, max=4, step=0.1, value=2))
<function __main__.lin_sep_svm_demo>
Linearly non-separable case¶
Linearly non-separable case¶
- Previous constraints become incomplatible!
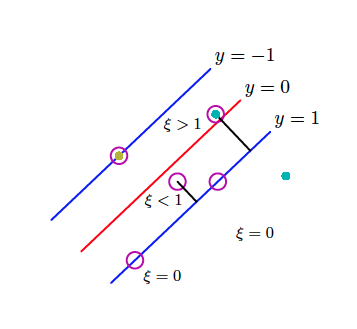
- Allow objects to get inside the street:
- Instead of $y_i(\langle w, x_i \rangle + w_0 ) \geq 1$
- Put $y_i(\langle w, x_i \rangle + w_0 ) \geq 1 - \xi_i, \quad \xi_i \geq 0$
And maximize:
$$ \frac{1}{2} ||w||^2 + C\sum\limits_i\xi_i \rightarrow \min\limits_{w,w_0,\xi} $$Linearly non-separable case¶
That brings us to the following optimization task: $$ \begin{cases} \frac{1}{2} ||w||^2 + C\sum\limits_i\xi_i \rightarrow \min\limits_{w,w_0,\xi} \\ y_i(\langle w, x_i \rangle + w_0 ) \geq 1 - \xi_i \quad i=1\dots n \\ \xi_i \geq 0 \quad i=1\dots n \end{cases} $$
- $C$ - is hyperparameter of missclassification cost
Linearly non-separable case: dual problem¶
With the same procedures we have the following dual problem $$\begin{cases} \mathcal{L}(\lambda) = \sum\limits_i\lambda_i - \frac{1}{2} \sum\limits_i\sum\limits_j \lambda_i \lambda_j y_i y_j (\langle x_i, x_j \rangle) \rightarrow \max\limits_\lambda \\ 0 \leq \lambda_i \leq C \quad i=1\dots n \\ \sum\limits_i \lambda_iy_i = 0 \end{cases}$$
interact(lin_sep_svm_demo_C, class_sep=FloatSlider(min=0.2, max=4, value=2, step=0.2), C=FloatSlider(min=0.002, max=10, step=0.002, value=1))
<function __main__.lin_sep_svm_demo_C>
Another view on SVM¶
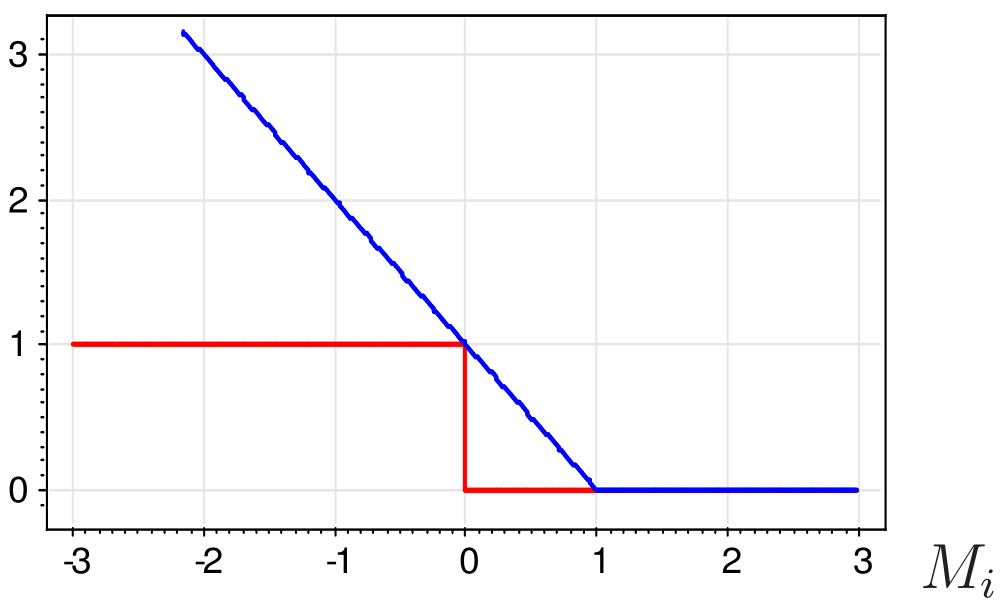
Problem $$ \begin{cases} \frac{1}{2} ||w||^2 + C\sum\limits_i\xi_i \rightarrow \min\limits_{w,w_0,\xi} \\ y_i(\langle w, x_i \rangle + w_0 ) \geq 1 - \xi_i \quad i=1\dots n \\ \xi_i \geq 0 \quad i=1\dots n \end{cases} $$ can be rewritten as $$ \frac{1}{2С} ||w||^2 + \sum\limits_i\max(0,1-M_i) \rightarrow \min\limits_{w,w_0}, $$ where $M_i$ - is margin of object $x_i$
Kernel Trick¶

demo_nonlin_data()
Transformation to linear separable domain¶
- $\phi: X \rightarrow H$
- $H$ - higher dimentional space in which classes become linearly separable
- Discrimenant function in $H$ is linear, but its projection on $X$ is not linear
Kernel Trick¶
- Imagine we try to fit SVM в $H$ $$\begin{cases} \mathcal{L}(\lambda) = \sum\limits_i\lambda_i - \frac{1}{2} \sum\limits_i\sum\limits_j \lambda_i \lambda_j y_i y_j (\langle \phi(x_i), \phi(x_j) \rangle) \rightarrow \max\limits_\lambda \\ 0 \leq \lambda_i \leq C \quad i=1\dots n \\ \sum\limits_i \lambda_iy_i = 0 \end{cases}$$
- No need to explicitly define $\phi$, only scalar product required!
- Kernel trick!
- $K(x_i, x_j) = \langle \phi(x_i), \phi(x_j) \rangle$ - kernel
Discriminant function:
- Without kernel $g(x) = w^\top x + w_0, \quad w = \sum\limits_{i:\lambda_i>0} \lambda_iy_ix_i$
- With kernel $g(x) = \sum\limits_{i:\lambda_i>0} \lambda_iy_i\langle x_i, x \rangle + w_0 = \sum\limits_{i:\lambda_i>0} \lambda_iy_i K(x_i, x) + w_0$
Kernel example¶
Polynomial type kernel $$ \begin{eqnarray*} K(x,z) & = & (x^{T}z)^{2}=(x_{1}z_{1}+x_{2}z_{2})^{2}=\\ & = & x_{1}^{2}z_{1}^{2}+x_{2}^{2}z_{2}^{2}+2x_{1}z_{1}x_{2}z_{2}\\ & = & \phi^{T}(x)\phi(z) \end{eqnarray*} $$
for $\phi(x)=(x_{1}^{2},x_{2}^{2},\sqrt{2}x_{1}x_{2})$
Kernel example¶
Polynomial type kernel $$ \begin{eqnarray*} K(x,z) & = & (1+x^{T}z)^{2}=(1+x_{1}z_{1}+x_{2}z_{2})^{2}=\\ & = & 1+x_{1}^{2}z_{1}^{2}+x_{2}^{2}z_{2}^{2}+2x_{1}z_{1}+2x_{2}z_{2}+2x_{1}z_{1}x_{2}z_{2}\\ & = & \phi^{T}(x)\phi(z) \end{eqnarray*} $$ for $\phi(x)=(1,\,x_{1}^{2},\,x_{2}^{2},\,\sqrt{2}x_{1},\,\sqrt{2}x_{2},\,\sqrt{2}x_{1}x_{2})$
Kernel properties¶
Mercer Theorem
Function $K(u, v)$ is a kernel iff
- it is symmetric $K(u, v) = K(v, u)$
- it is non-negatively defined:
- $ \int_X \int_X K(u,v) f(u)f(v) du dv \geq 0$, $\forall f: X \rightarrow \mathbb{R}$
- Gramm matrix $\left\{ K(x_i, x_j) \right\} \geq 0$ (p.s.d)
We can construct new kernels from other kernels
- Dot product is kernel $K(u,v) = \langle u, v \rangle$
- Constant is kernel, $K(u,v) = 1$
- $\forall \phi: X \rightarrow \mathbb{R}$ product $K(u,v) = \phi(u) \phi(v)$ - is kernel
- $K(u,v) = \alpha_1K_1(u,v) + \alpha_2K_2(u,v) $ - kernel
- $K(u,v) = K_1(u,v) \cdot K_2(u,v) $ - kernel
- $\forall \psi: X \rightarrow X \quad K(u,v) = K'(\psi(u),\psi(v)) $ - kernel
- $e^{K(u,v)}$ - kernel
Commonly used kernels¶
- Linear: $$\langle x, y\rangle$$
- Polynomial: $$(\gamma \langle x, y\rangle + с)^d,$$
- Radial basis function kernel (rbf): $$e^{(-\gamma \cdot \|x - y\|^2)},$$
- Sigmoid: $$\tanh(\gamma \langle x,y \rangle + r)$$
YouTubeVideo('3liCbRZPrZA', width=640, height=480)
interact(lin_sep_svm_demo_kernel_C, class_sep=FloatSlider(min=0.2, max=4, value=2, step=0.2), kernel=['rbf', 'linear', 'poly'], coef0=FloatSlider(min=0, max=10, step=0.2, value=0), C=FloatSlider(min=0.002, max=10, step=0.002, value=1), degree=FloatSlider(min=2, max=3, step=1, value=2), gamma=FloatSlider(min=0.01, max=5, step=0.01, value=0.5),)
<function __main__.lin_sep_svm_demo_kernel_C>
SVM for regression!¶
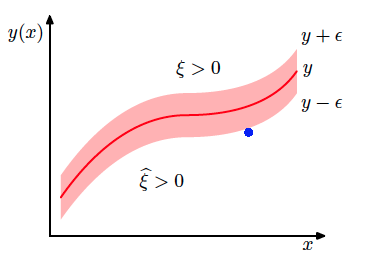
SVM for regression!¶
$\xi_i \geq 0$, $\hat \xi_i \geq 0$ - slacks: $$ y_i \leq g(x_i) + \epsilon + \xi_i $$ $$ y_i \geq g(x_i) - \epsilon - \hat \xi_i $$
Optimization task
$$ \begin{cases} C \sum_{i=1}^n (\hat \xi_i + \xi_i) + \frac{1}{2}\|w\|^2 \rightarrow \min\limits_{w, w_0} \\ g(x_i) - y_i \leq \epsilon + \xi_i \\ y_i - g(x_i) \leq \epsilon + \hat{\xi}_i \\ \xi_i \geq 0, \hat \xi_i \geq 0 \end{cases} $$Some SVM tutorials and materials: