Data Analysis
Andrey Shestakov (avshestakov@hse.ru)
Ensembles.1
1. Some materials are taken from machine learning course of Victor Kitov
Ensembles¶
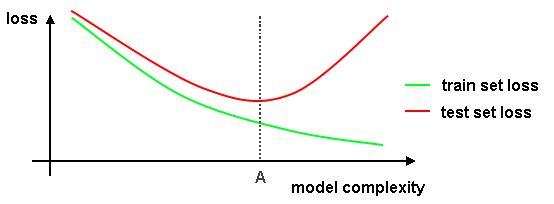
Bias-variance decomposition¶
Bias-variance decomposition¶
- Consider regression task and MSE
- Let $y$ - be target features, $x$ - are predictors
- True relationship: $ y(x) = f(x) + \epsilon $ where $ \epsilon $ is gaussian white noise, $\epsilon \sim \mathcal{N}(0,\sigma^2) $
- Model: $ a(x) = \hat{y} $.
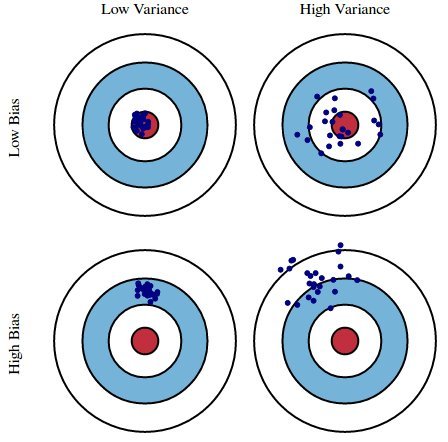
Those components can be interpreted as
- $\text{Variance}$ (Разброс) - model's sensivity to dataset. High variance usually means that model is overfitted.
- $\text{Bias}$ (Смещение) - is in charge of model's precision. High bias usually means that model is underfitted.
- $\text{Noise}$ (Шум) - that is just noise
Bias and variance¶
Bias-variance decomposition¶
Define for brevity of notation $y(x)=y,\, a(x) = a,\, f(x) = f, \, \mathbb{E}=\mathbb{E}_{X,Y,\varepsilon}$:
\begin{equation} \begin{split} \text{Error} & = \mathbb{E}\left[(a - y)^2\right] = \mathbb{E}\left[a^2 - 2ay + y^2\right] = \\ & = \underbrace{\mathbb{E}\left[(a - \mathbb{E}[a])^2\right] + \mathbb{E}[a]^2}_{=\mathbb{E}[a^2]} - 2\mathbb{E}[ay] + \underbrace{\mathbb{E}\left[(y - \mathbb{E}[y])^2\right] + \mathbb{E}[y]^2}_{=\mathbb{E}[y^2]} = \\ & = \mathbb{E}\left[(a - \mathbb{E}[a])^2\right] + \left(\mathbb{E}\left[a\right] - f\right)^2 + \mathbb{E}\left[(y - f)^2\right] = \\ & = \text{Variance} + \text{Bias}^2 + \text{Noise} \end{split} \end{equation}Ensemble learning¶
Ensemble learning - using multiple machine learning methods for a given problem and integrating their output to obtain final result
Synonyms: committee-based learning, multiple classifier systems.
Applications:
- supervised methods: regression, classification
- unsupervised methods: clustering
Ensembles use cases¶
underfitting, high model bias
- existing model hypothesis space is too narrow to explain the true one
- different oversimplified models have bias in different directions, mutually compensating each other.
overfitting, high model variance
- avoid local optima of optimization methods
- too small dataset to figure out concretely the exact model hypothesis
- when task itself promotes usage of ensembles with features of different nature
- E.g. computer security:
- multiple sources of diverse information (password, face detection, fingerprint)
- different abstraction levels need to be united (current action, behavior pattern during day, week, month)
- E.g. computer security:
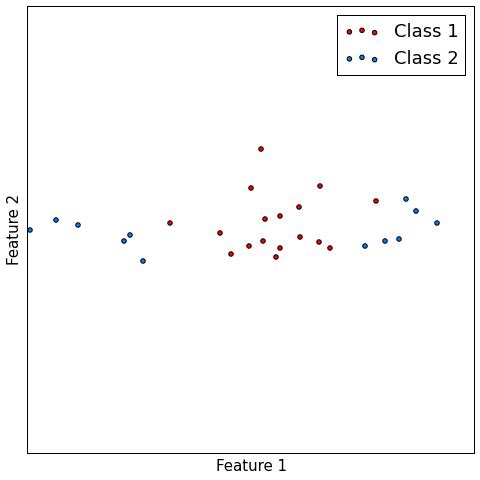
Accuracy improvement demos¶
Classification¶
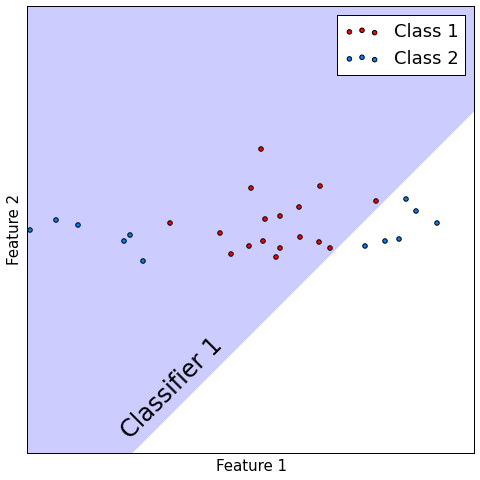
Classification¶
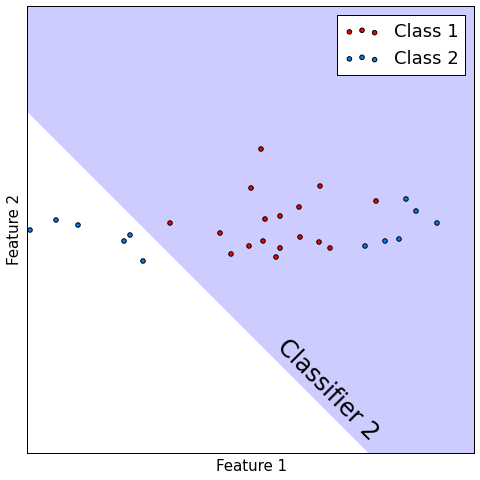
Classification¶
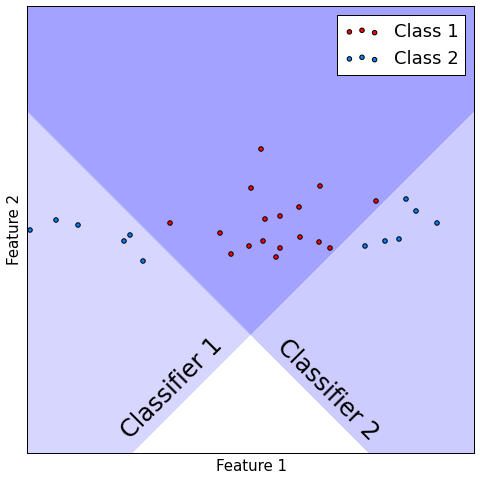
Classification¶
Classification¶
- Consider $M$ classifiers $f_{1}(x),...f_{M}(x)$, performing binary classification.
- Let probability of correct precision be constant $p\in(\frac{1}{2}, 1)$: $p(f_{m}(x)=y)=p\,\forall m$
- Suppose all models make mistakes or correct guesses independently of each other.
- Let $F(x)$ be majority voting combiner.
- Then $p(F(x) = y)\to1$ as $m\to\infty$
M = 50
T = M//2 + 1
p = 0.6
p_ens = sum([scipy.misc.comb(M,k)*(p**k)*((1-p)**(M-k)) for k in range(T, M+1)])
p_ens
0.9021926358467505
Regression¶
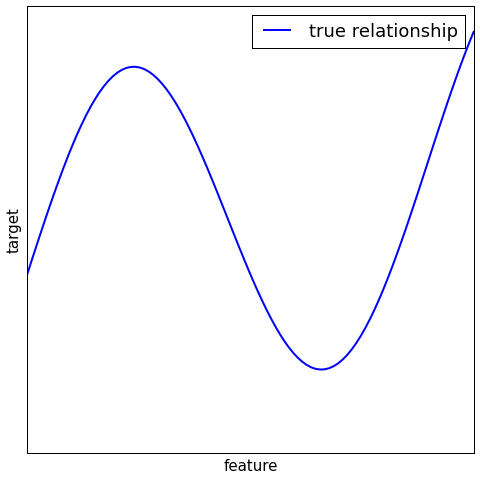
Regression¶
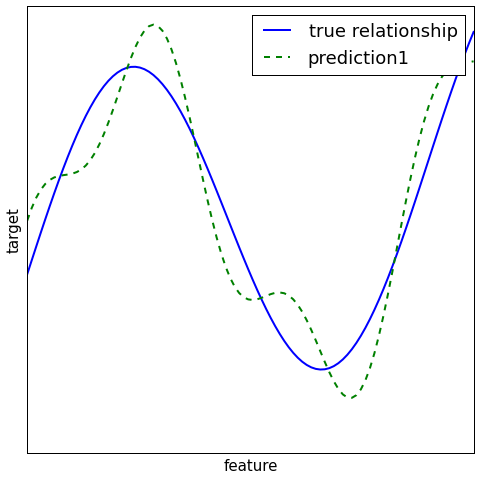
Regression¶
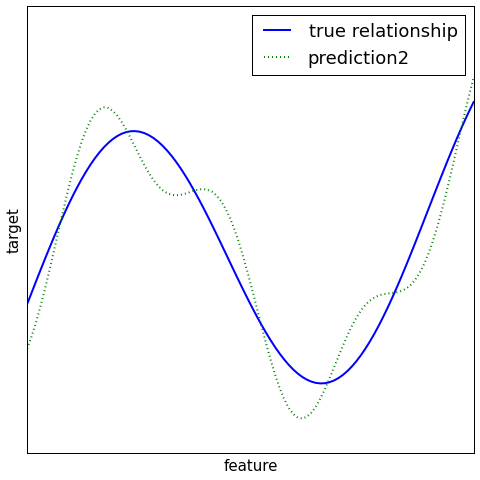
Regression¶
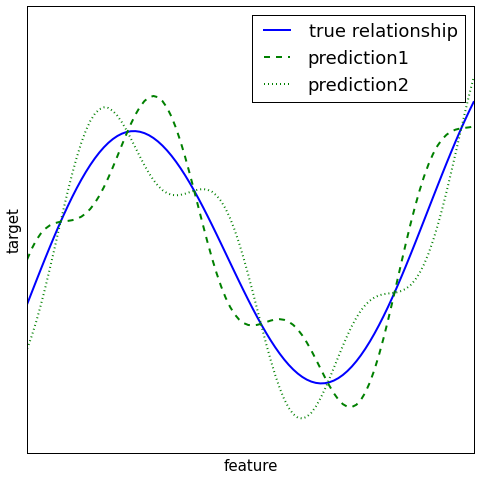
Fixed integration schemes for classification¶
Fixed integration schemes for classification¶
Output of base learner k: exact class: $\omega_{1}$ or $\omega_{2}$.
Combiner predicts $\omega_{1}$ if:
- all classifiers predict $\omega_{1}$ (AND rule)
- at least one classifier predicts $\omega_{1}$ (OR rule)
- at least $k$ classifiers predict $\omega_{1}$ (k-out-of-N)
- majority of classifiers predict $\omega_{1}$ (majority vote)
Each classifier may be assigned a weight, based on its performance:
- weighted majority vote
- weighted k-out-of-N (based on score sum)
Fixed combiner - ranking level¶
Output of base learner k:
Ranking of classes: $$ \omega_{k_{1}}\succeq\omega_{k_{2}}\succeq\ldots\succeq\omega_{k_{C}} $$
Ranking is equivalent to scoring of each class (with incomparable scoring between classifiers).
Definition
Let $B_{k}(i)$ be the count of classes scored below $\omega_{i}$
by classifier $k$.
Borda count $B(i)$ of class $\omega_{i}$ is the total number of classes scored below $\omega_{i}$ by all classifiers: $$ B(i)=\sum_{k=1}^{K}B_{k}(i) $$
Combiner predicts $\omega_{i}$ where $i=\arg\max_{i}B(i)$
Fixed combiner at class probability level¶
Output of base learner k: vectors of class probabilities: $$ [p^{k}(\omega_{1}),\,p^{k}(\omega_{2}),\,\ldots\,p^{k}(\omega_{C})] $$
Combiner predicts $\omega_{i}$ if $i=\arg\max_{i}F(p^{1}(\omega_{i}),p^{2}(\omega_{i}),\ldots p^{K}(\omega_{i}))$
- $F$ = mean or median.
Sampling ensemble methods¶
Sampling ensembles¶
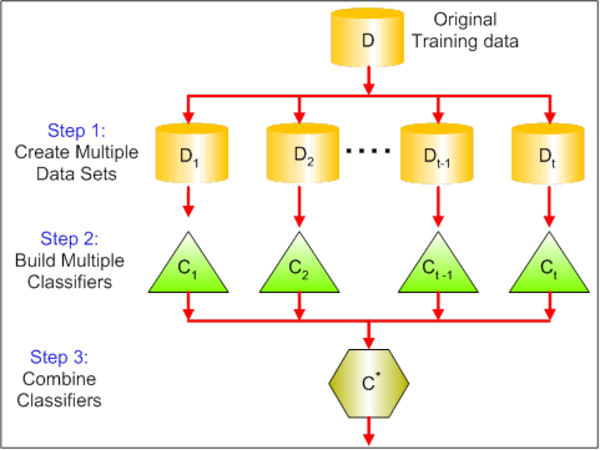
How bagging affects bias-variance decomposition?¶
Intuitively, bagging should reduce variance
- Consider $z_1,\dots,z_n~Z$, i.i.d., $\mathbb{E}[Z] = \mu$, $Var[Z] = \sigma^2$
- How can we estimate $\mu$?
- We can use any single $z_i$, but it would be quite uncertain, since $Var[z_i] = \sigma^2$
- What about $\frac{1}{n}\sum_i z_i$ ?
- $\mathbb{E}\left[\frac{1}{n}\sum\limits_i z_i\right] = \mu$, but!
- $Var\left[\frac{1}{n}\sum\limits_i z_i\right] = \frac{1}{n^2}Var\left[\sum\limits_i z_i\right] = \frac{1}{n}\sigma^2$
- Variance of that estimation is lower
- Say we have $n$ independent training sets from the same distribution
- Learning $n$ alorithms on them would provide us with $n$ decision functions $a_i(x)$
- Average prediction of an object $x$ is $$ a_{avg}(x) = \frac{1}{n}\sum_{i=1}^n a_i(x)$$
- $\mathbb{E}[a_{avg}(x)] = \mathbb{E}[a_1(x)]$
- $Var[a_{avg}(x)] = \frac{1}{n}Var[a_1(x)]$
- ...
- Profit (?)
Bagging¶
- Need a way to make independent training sets (independent decision functions)
- One of the ways is bootstrap:
- Generate $B$ datasets from original $X$ using sampling with replacements - $X_i$
- Each generated dataset contains about $67\%$ of original dataset
- Train a model $a_i(x)$ on each dataset
- Average their preditions

Random forests¶

Random forests¶
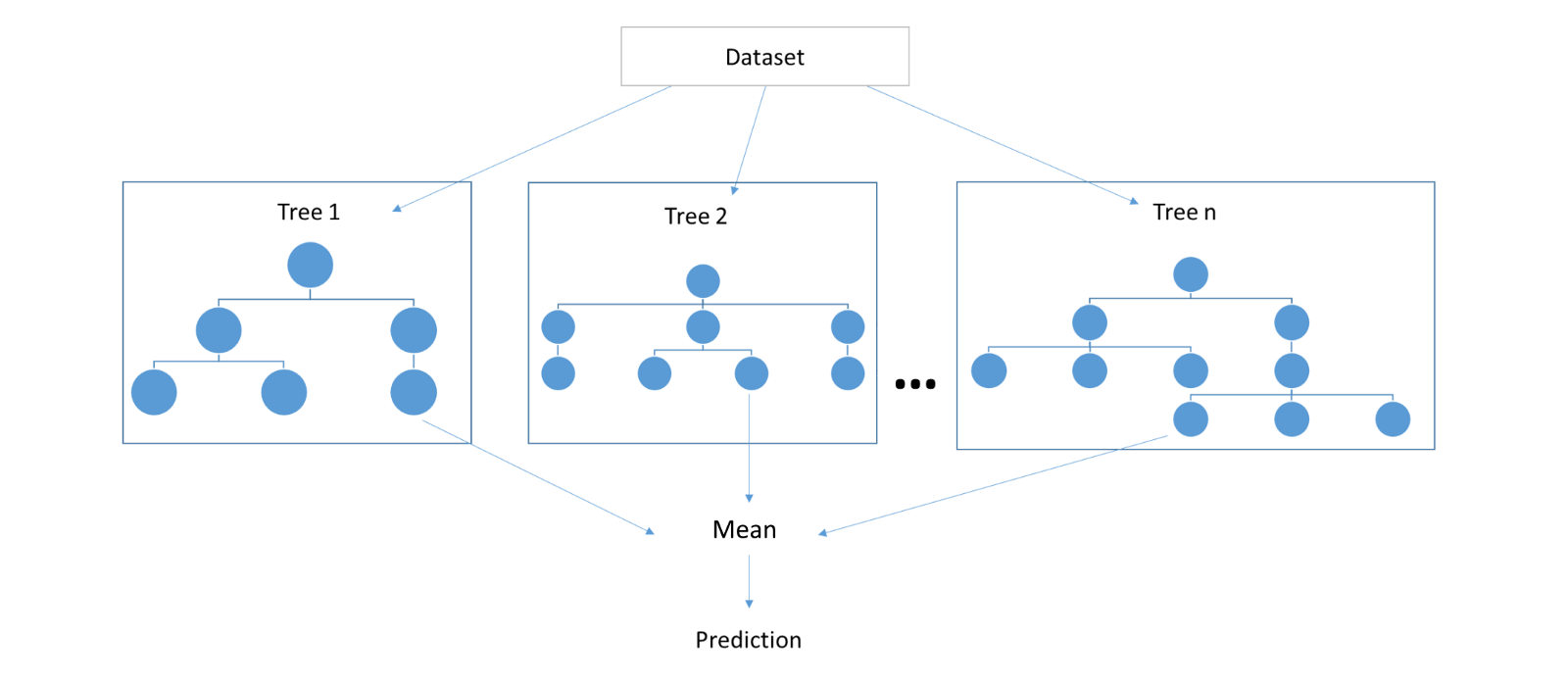
Random forests¶
- In fact, bootstraped datasets are not independent w.r.t. $p(x,y)$
- Random forests tries to make trees even more independent through randomization in construction algorithm
Input:
- training dataset $TDS=\{(x_{i},y_{i}),\,1=1,2,...N\}$;
- the number of trees $B$ and the size of feature subsets $m$.
for $b=1,2,...B$:
- generate random training dataset $TDS^{b}$ of size $N$ by sampling $(x_{i},y_{i})$ pairs from $TDS$ with replacement (bootstrap)
- build a tree using $TDS^{b}$ training dataset with feature selection for each node from random subset of features of size $m$ (generated individually for each node).
Output: $B$ trees. Classification is done using majority vote and regression using averaging of $B$ outputs
Comments¶
- Random forests use random selection on both samples and features
Left out samples may be used for evaluation of model performance.
- Out-of-bag prediction: assign output to $x_{i}$, $i=1,2,...N$ using majority vote (classification) or averaging (regression) among trees with $b\in\{b:\,(x_{i},y_{i})\notin T^{b}\}$
- Out-of-bag quality - lower bound for true model quality.
Less interpretable than individual trees
- Parallel implementation
- Different trees are not targeted to correct mistakes of each other
Comments¶
Extra-Random trees-random sampling of (feature,value) pairs
- more bias and less variance for each tree
- faster training of each tree
RandomForest and ExtraRandomTrees do not overfit with increasing $B$
- Each tree should have high depth
- otherwise averaging over oversimplified trees will also give oversimplified model!
- Demo
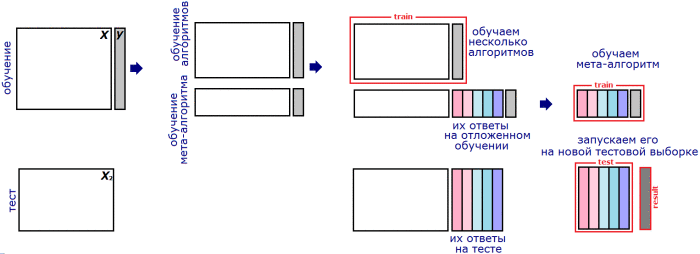
Stacking and blending¶
Stacking¶
Weighted averaging¶
Consider regression with $K$ predictor models $f_{k}(x)$, $k=1,2,...K$.
(Alternatively we may consider $K$ discriminant functions in classification)
Weighted averaging combiner
$$
f(x)=\sum_{k=1}^{K}w_{k}f_{k}(x)
$$
Naive fitting $$ \widehat{w}=\arg\min_{w}\sum_{i=1}^{N}\mathcal{L}(y_{i},\sum_{k=1}^{K}w_{k}f_{k}(x_{i})) $$
overfits. The mostly overfitted method will get the most weight.
Linear stacking¶
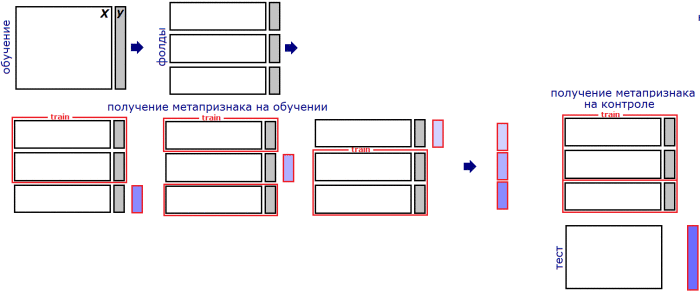
- Let training set $\{(x_{i},y_{i}),i=1,2,...N\}$ be split into $M$ folds.
- Denote $fold(i)$ to be the fold, containing observation $i$
- Denote $f_{k}^{-fold(i)}$ be predictor $k$ trained on all folds, except $fold(i)$.
Definition</br>
Linear stacking is weighted averaging combiner, where weights are found using $$ \widehat{w}=\arg\min_{w}\sum_{i=1}^{N}\mathcal{L}(y_{i},\sum_{k=1}^{K}w_{k}f_{k}^{-fold(i)}(x_{i})) $$
General stacking¶
Definition
Generalized stacking is prediction $$ f(x)=A_{\theta}\left(f_{1}(x),f_{2}(x),\ldots f_{K}(x)\right), $$
where $A$ is some general form predictor and $\theta$ is a vector of parameters, estimated by $$ \widehat{\theta}=\arg\min_{\theta}\sum_{i=1}^{N}\mathcal{L}\left(y_{i},\,A_{\theta}\left(f_{1}^{-fold(i)}(x),f_{2}^{-fold(i)}(x),\ldots f_{K}^{-fold(i)}(x)\right)\right) $$
- Stacking is the most general approach
- It is a winning strategy in most ML competitions.
- $f_{i}(x)$ may be:
- class number (coded using one-hot encoding).
- vector of class probabilities
- any initial or generated feature
- See this for additional details