Data Analysis

Andrey Shestakov (avshestakov@hse.ru)

Intoduction1

1. Materials used from machine learning course of Victor Kitov

Some Friendly Faces

Lectures: Andrey Shestakov
 Seminars: Mikhail Gushin
 Seminars: Radomir Britkov
Seminars: Leyla Khatbullina
 Seminars: Leonid Matyushin

TAs: Natalia Zubkova, Anna Starovoyt, Anna Karbovskaya

Course information

  • Structure:

    • lectures, seminars
    • practical assignments (anytask), competitions (kaggle)
    • midterm colloquium
    • exam

  • Evaluation:

    • cumulative score = 0.8 $S_{\text{homework}}$ + 0.2 $S_{\text{colloq}}$+ 0.2 * $S_{\text{competition}}$
    • score = 0.7 $S_{\text{cumulative}}$ + 0.3 $S_{\text{exam}}$

  • Tools

    • python 3
    • Jupyter Notebook
    • numpy, scipy, pandas
    • matplotlib, seaborn
    • scikit-learn and more

Recommended materials

  • Any additional public sources:
    • wikipedia, articles, tutorials, video-lectures.

Plan 4 today

  • Motivation to learn data analysis (data science, machine learning)
  • Get used to some notations
  • Problem types
  • Feature types
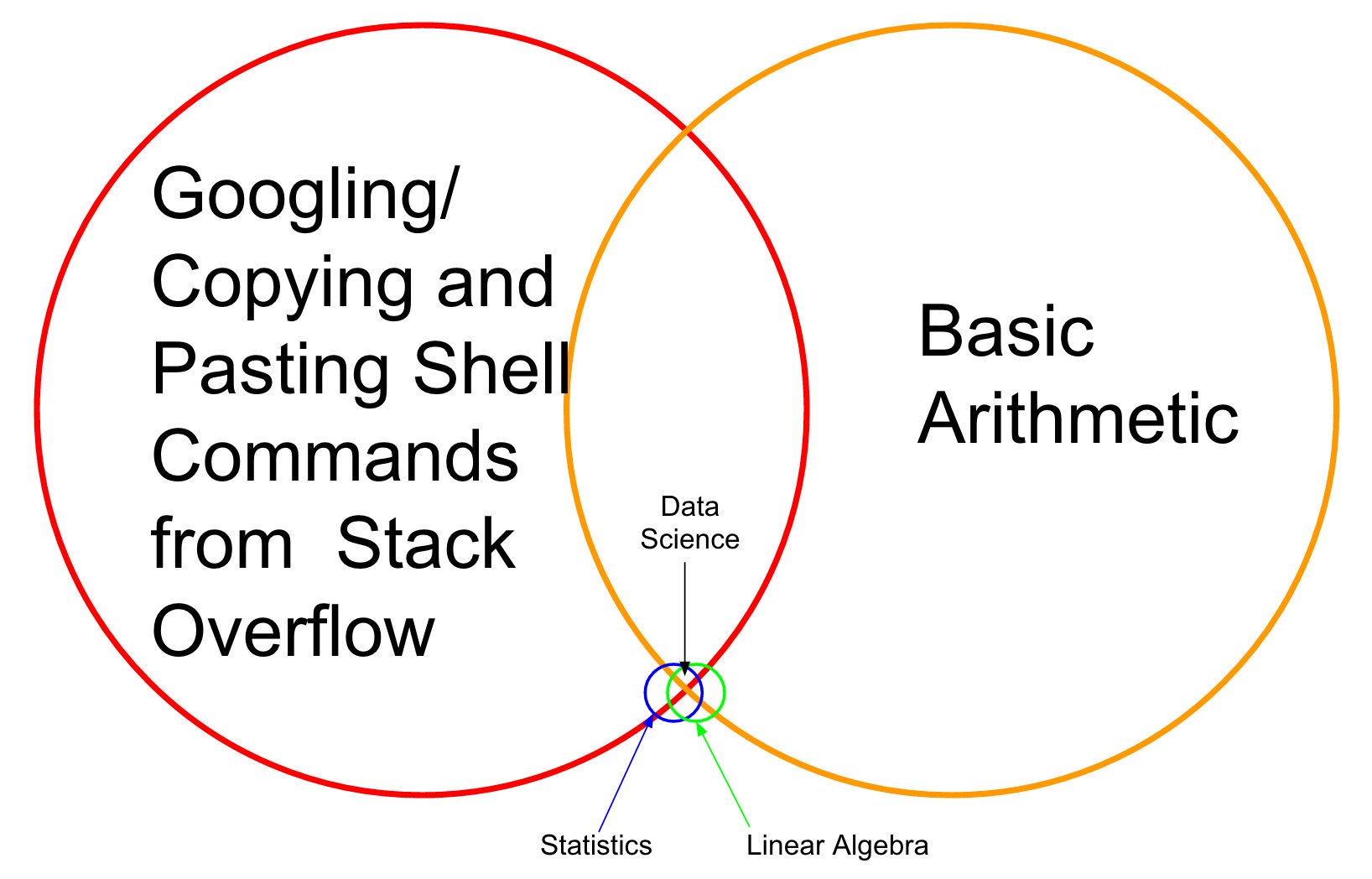
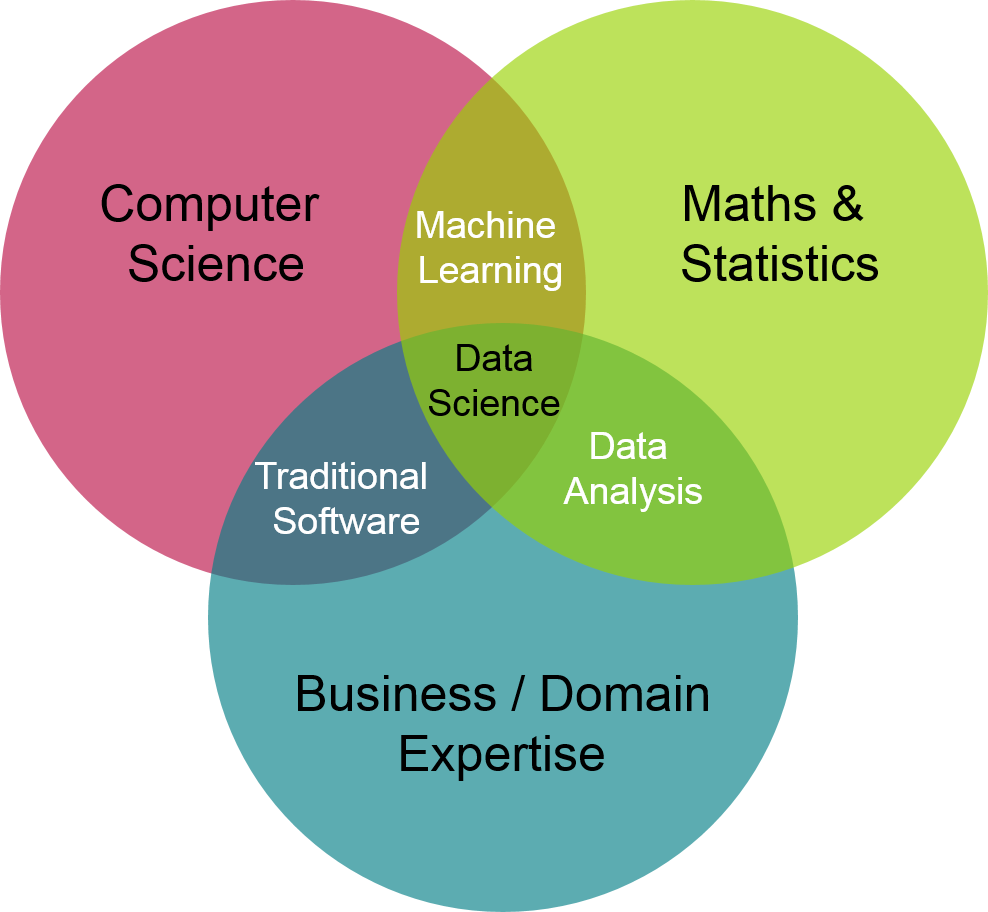
  • Some fundamental terminology, pics and memes

Motivation

Motivation

Motivation

In [3]:
YouTubeVideo('zvGeLvWZ7yQ', width=700, height=600)
Out[3]:

Motivation

50 years of data science

Motivation

  • Data scientist is a highly wanted and well-paid specialization.
  • Apply boring calculus, linear algebra and statistics to problem solving.
  • Should use machine learning "apparatus" to extract knowledge from data.

Machine learning?

  • Machine learning is a field of study that gives computers the ability to learn without being explicitly programmed.

Examples

  • Spam filtering

    • if sender belongs to black-list -> spam
    • if contains phrase 'buy now' and sender is unknown -> spam
    • ...

  • Part-of-speech tagger.

    • if ends with 'ed' -> verb
    • if previous word is 'the' -> noun
    • ...
  • ML finds decision rules automatically with labelled data!

Formal problem statement

  • Set of objects $O$
  • Each object is described by a vector of known characteristics $\mathbf{x}\in\mathcal{X}$ and predicted characteristics $y\in\mathcal{Y}$. $$ o\in O\longrightarrow(\mathbf{x},y) $$
  • Task: find a mapping $f$, which could accurately approximate $\mathcal{X}\to\mathcal{Y}$.
    • using a finite known set of objects (learning)
    • apply model for objects from the test set (prediction)
    • understand revealed relationships in data (inference, interpretation)

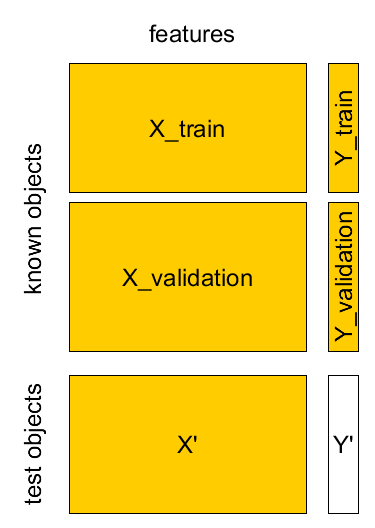
Known Set

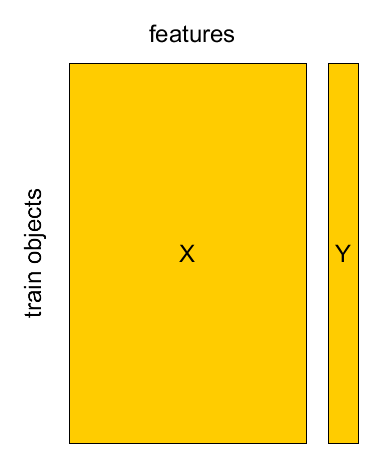
Known set: $(\mathbf{x}_{1},y_{1}),...(\mathbf{x}_{M},y_{M})$
design matrix $X=[\mathbf{x}_{1},...\mathbf{x}_{M}]^{T}$, $Y=[y_{1},...y_{M}]^{T}$.

Known Set

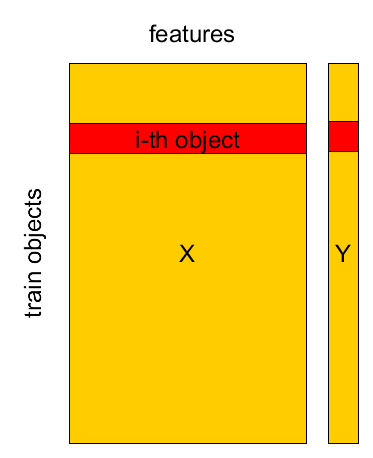
Known set: $(\mathbf{x}_{1},y_{1}),...(\mathbf{x}_{M},y_{M})$
design matrix $X=[\mathbf{x}_{1},...\mathbf{x}_{M}]^{T}$, $Y=[y_{1},...y_{M}]^{T}$.

Known Set

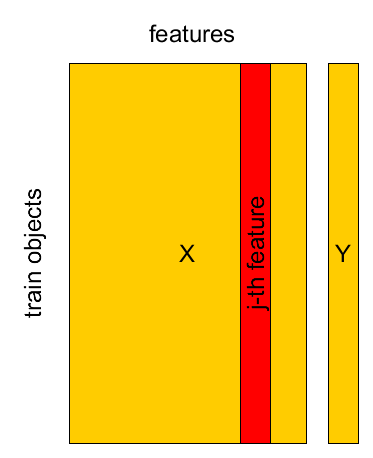
Known set: $(\mathbf{x}_{1},y_{1}),...(\mathbf{x}_{M},y_{M})$
design matrix $X=[\mathbf{x}_{1},...\mathbf{x}_{M}]^{T}$, $Y=[y_{1},...y_{M}]^{T}$.

Test set

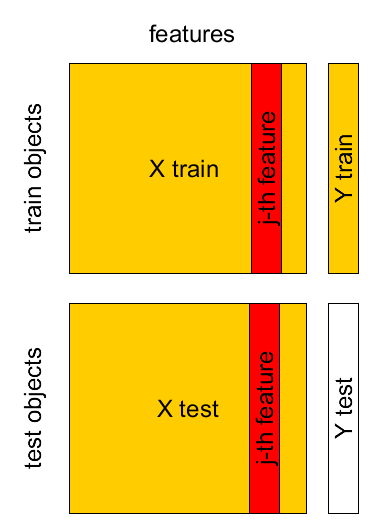
  • Known sample $X,Y$: $(\mathbf{x}_{1},y_{1}),...(\mathbf{x}_{M},y_{M})$
  • Test sample $X',Y'$: $(\mathbf{x}_{1}',y_{1}'),...(\mathbf{x}_{K}',y_{K}')$

Specification of ML tasks

  • supervised learning: $(\mathbf{x}_{1},y_{1}),(\mathbf{x}_{2},y_{2}),...(\mathbf{x}_{N},y_{N})$
    • e.g. regression, classification.
  • unsupervised learning: $\mathbf{x}_{1},\mathbf{x}_{2},...\mathbf{x}_{N}$
    • e.g. dimensionality reduction, clustering, outlier analysis, topic modelling

Toy examples

Regression 1

Predict $y\in\mathbb{R}$ for any $x$

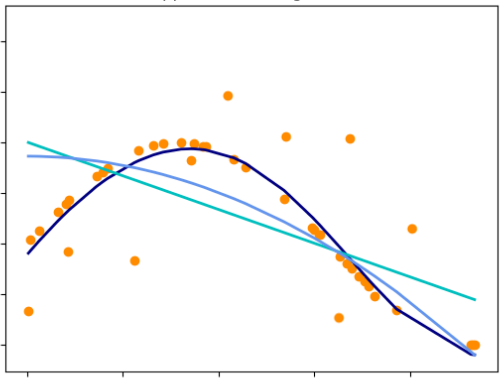
Regression 2

  • Obviously, those characteristics somehow relate with price ($f: X \rightarrow Y$)
  • Formalize a model to predict flat price: $$a(x) = a(total\_area, nmbr\_of\_bedrooms, house\_age) = \hat{y}$$
  • Let it be a linear model: $$a(x) = w_0 + w_1\cdot total\_area + w_2 \cdot nmbr\_of\_bedrooms + w_3 \cdot house\_age$$
  • Learning - find coefficients $w_0,\dots, w_3$, that minimizer error on training set

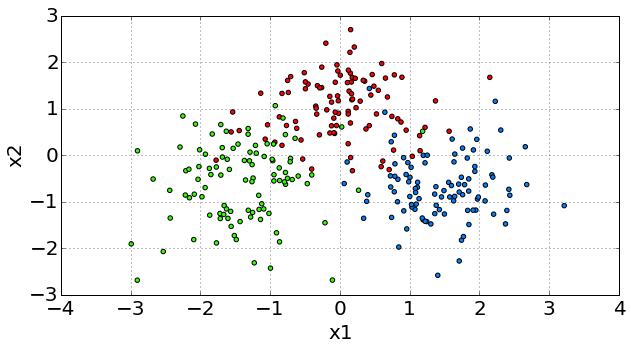
Classificaion 1

Predict class $y$ shown with color for any point.

Classification 2

Inbox message classification

Help user organize email inbox

  • Natual Language Processing

Unsupervised Learning. Clustering

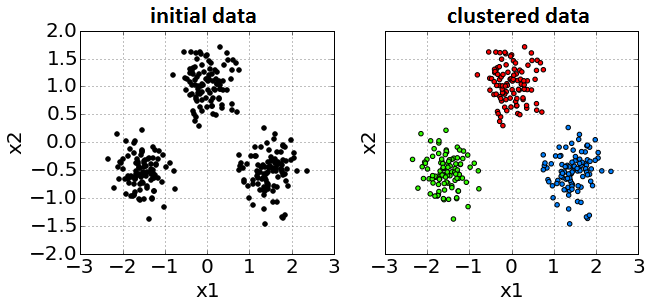
Clustering

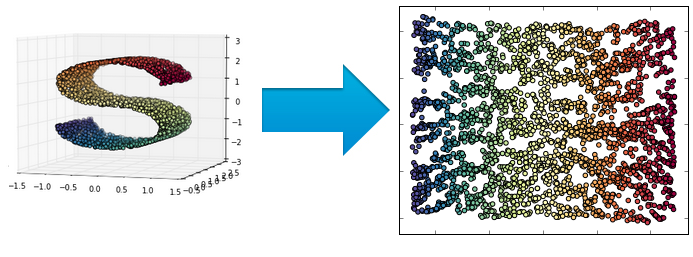
Unsupervised Learning. Dimensionality reduction

Reduce dimension from 3D to 2D with minimal distortion.

Unsupervised Learning. Topic modelling

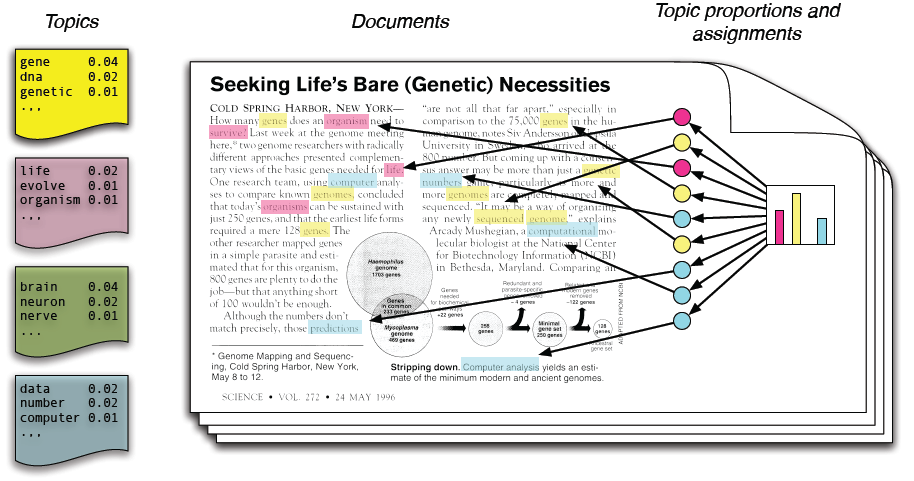
Describe huge document with a low-dimentional sparse vector

Outlier Detection Task

Detect untypical observations.

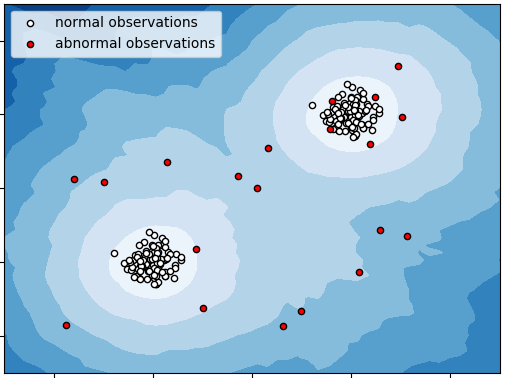
Recommender Systems

Recommender Systems

Ranking

Reinforcement learning

  • RL setup:
    • a set of environment and agent states $S$;
    • a set of actions $A$, of the agent
    • $P(s_{t+1}=s'|s_{t}=s,a_{t}=a)$ is the probability of transition from state s to state s' under action a.
    • $R_{a}(s,s')$ is the (expected) immediate reward after transition from $s$ to $s'$ with action $a$.
  • Well-suited to problems which include a long-term versus short-term reward trade-off
  • Applications: robot control, elevator scheduling, games (chess, go, DOTA), etc.
In [12]:
YouTubeVideo('V1eYniJ0Rnk', width=700, height=600)
Out[12]:

General Problem Statement

  • We want to approximate $f(x):\,X\to Y$

  • Questions in ML:

    • what target $y$ we are predicting?
    • how to select object descriptors (features) $x$?
    • what type of mapping $f$?
    • in what sense a mapping $f$ should approximate true relationship?
    • how to tune $f$?

What target $y$ we are predicting?

Types of target variable (supervised learning)

  • $\mathcal{Y}=\mathbb{R}$ - regression
    • e.g. flat price
  • $\mathcal{Y}=\mathbb{R}^{M}$ - vector regression
    • e.g. stock price dynamics

Types of target variable (supervised learning)

  • $\mathcal{Y}=\{\omega_{1},\omega_{2},...\omega_{C}\}$ - classification.
    • C=2: binary classification.
    • e.g. spam / not spam (ham)
  • C>2: multi-class classification
    • e.g. identity recognition, activity recognition
  • $\mathcal{Y}$ - any subset of $\{\omega_{1},\omega_{2},...\omega_{C}\}$ - labeling
    • e.g. news categorization

How to select object descriptors (features) 𝑥?

Types of features

  • Full object description $\mathbf{x}\in\mathcal{X}$ consists of individual features $x^{i}\in\mathcal{X}_{i}$
  • Types of feature (e.g. for credit scoring):
    • $\mathcal{X}_{i}=\{0,1\}$ - binary feature
      • e.g. marital status
    • $|\mathcal{X}_{i}|<\infty$ - categorical (nominal) feature
      • e.g. occupation
    • $|\mathcal{X}_{i}|<\infty$ and $\mathcal{X}_{i}$ is ordered - ordinal feature
      • e.g.education level
    • $\mathcal{X}_{i}=\mathbb{R}$ - continuous feature
      • e.g. age

Credit scoring

  • Objects — credit applicantion
  • Target — return credit of not
  • Kind of task and features?

Credit scoring

  • Binary: sex,
  • Categorical: living region, profession, marital status
  • Ordinal: education level, work grade
  • Continuous: age, wage

Churn prediction

  • Object — online game user
  • Target — will he/she lose interest in playing after 2 weeks?
  • Kind of task and features?

Churn prediction

  • Binary: premium user
  • Categorical: avatar class, game plan
  • Continuous: average playing hours per day, number of characters, chat activity

What type of mapping 𝑓?

In what sense a mapping 𝑓 should approximate true relationship?

Learning = Representation + Evaluation + Optimization

A Few Useful Things to Know about Machine Learning // Pedro Domingos

Model Class (Representation)

Linear Example

  • Function class - parametrized set of functions $F=\{f_{\theta},\,\theta\in\Theta\}$, from which the true relationship $\mathcal{X}\to\mathcal{Y}$ is approximated.
    • Regression: $\widehat{y}=f(x|\theta)$,
    • Classification: $\widehat{y}=f(x|\theta)=\arg\max_{c}\left\{ g_{c}(x|\theta)\right\} $, $c=1,2,...C$.
      • $c=1,2,...C$: possible classes, $g_{c}(x)$ - score of class $c$, given $x$ called discriminant function

Examples

linear regression $y\in\mathbb{R}$: $$f(x\mathbf{|\theta})=\theta_{0}+\theta_{1}x$$ 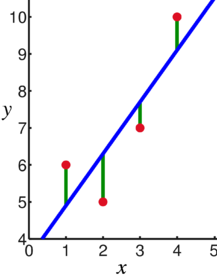linear classification $y\in\{1,2\}$: \begin{align*} g_{c}(\mathbf{x}|\theta) & =\theta_{c}^{0}+\theta_{c}^{1}x^{1}+\theta_{c}^{2}x^{2},\,c=1,2.\\ f(\mathbf{x|\theta}) & =\arg\max_{c}g_{c}(x|\theta) \end{align*}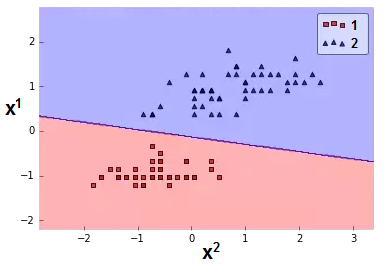

Loss function vs model quality (Evaluation)

  • In machine learning models try to optimize some function, which you can call:
    • score, rating - if you are maximizing
    • loss, cost, error - if you are minimized
    • both score and loss can be computed for individual objects
    • directly optimized in model
  • Model quality measures are used to compare diffrent models' performance on test set
    • some of them can not be directly optimized in the model
    • usually can not be computed for individual objects

Loss function $\mathcal{L}(\widehat{y},y)$

  • regression:
    • MAE (mean absolute error): $$ \mathcal{L}(\widehat{y},y)=\frac{1}{N}\sum\limits_i\left|\widehat{y}_i-y_i\right| $$
    • MSE (mean squared error): $$ \mathcal{L}(\widehat{y},y)=\frac{1}{N}\sum\limits_i\left(\widehat{y}_i-y_i\right)^{2} $$
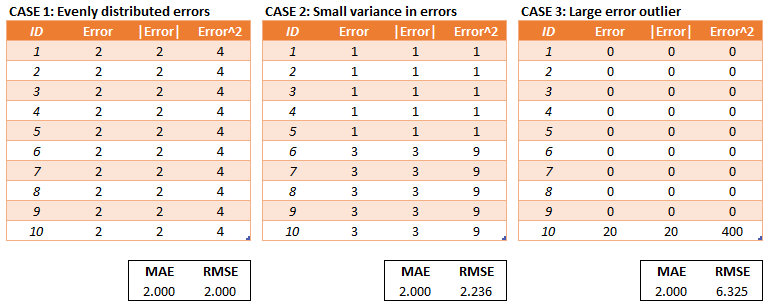
  • classification:
    • log-loss $$ \mathcal{L}(\widehat{y},y)=\mathbb{I}[y==1]\log\left(p(\hat{y} = 1)\right) + \mathbb{I}[y==-1]\log\left(p(\hat{y}=-1)\right) $$
In [11]:
plt.plot(h, L1, label='logloss if y = +1')
plt.plot(h, L2, label='logloss if y = -1')
plt.ylabel('logloss')
plt.xlabel('classifier probability of +1')

_ = plt.legend()

Optimization

How to tune $f$?

Overfitting - Underfitting

  • Theoretically, a very complex model can achive perfect quality on training dataset
  • Profit???
  • Nope...

Overfitting - Underfitting

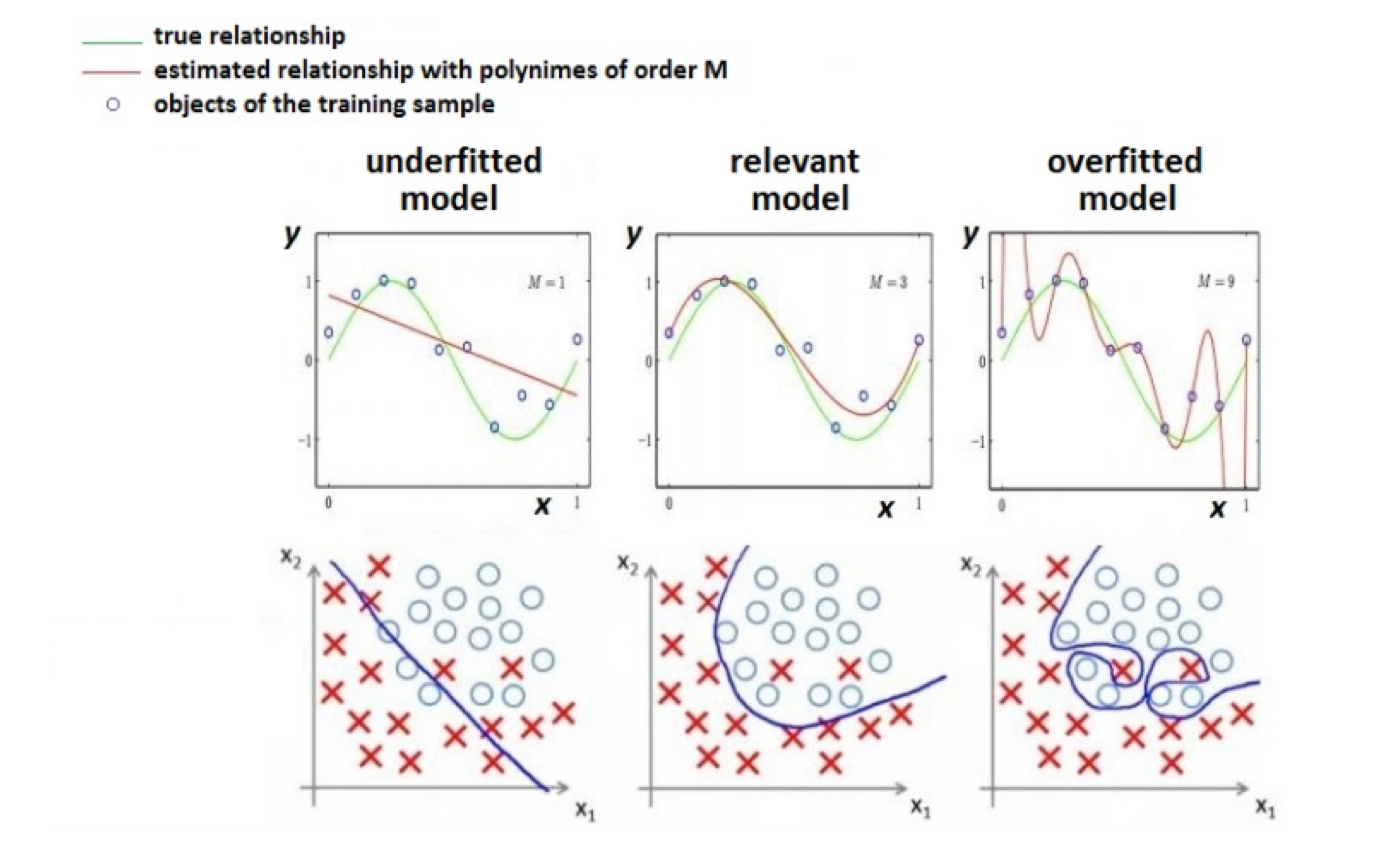
Empirical risk

  • Want to minimize expected risk: $$ \mathit{\int}\int\mathit{\mathcal{L}(f_{\theta}(\mathbf{x}),y) \cdot p(\mathbf{x},y)d\mathbf{x}dy\to\min_{\theta}} $$

  • In fact we have only $X$,$Y$ (Known set) and $X'$ (Test set)

  • Can minimize empirical risk $$ L(\theta|X,Y)=\frac{1}{N}\sum_{n=1}^{N}\mathcal{L}(f_{\theta}(\mathbf{x}_{n}),\,y_{n}) $$

  • Method of empirical risk minimization: $$ \widehat{\theta}=\arg\min_{\theta}L(\theta|X,Y) $$

  • How to get realistic estimate of $L(\widehat{\theta}|X',Y')$?
    • separate validation set
    • cross-validation
    • leave-one-out method

Separate validation set

  • Known sample $X,Y$: $(\mathbf{x}_{1},y_{1}),...(\mathbf{x}_{M},y_{M})$
  • Test sample $X',Y'$: $(\mathbf{x}_{1}',y_{1}'),...(\mathbf{x}_{K}',y_{K}')$

Separate validation set

Divide known set randomly or randomly with stratification:

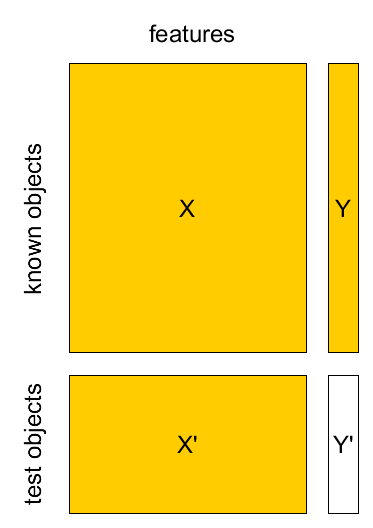
Cross-validation

4-fold cross-validation example

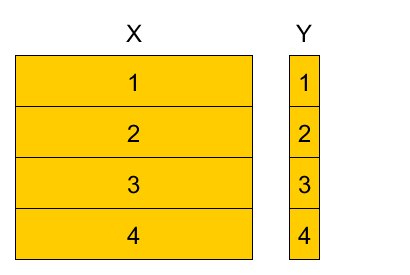
Divide training set into K parts, referred as folds (here $K=4$).

Variants:

  • randomly
  • randomly with stratification (w.r.t target value or feature value)
  • randomly with respect to time domain
  • etc

4-fold cross-validation example

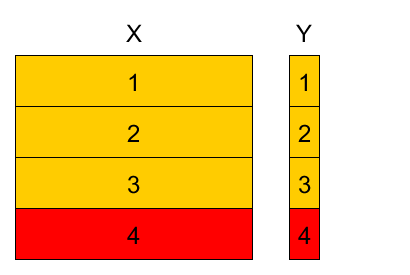
Use folds 1,2,3 for model estimation and fold 4 for model evaluation.

4-fold cross-validation example

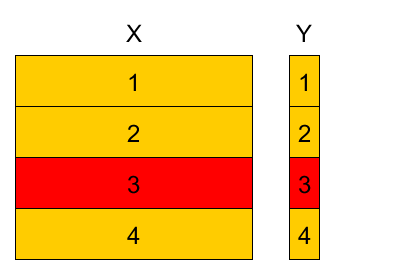
4-fold cross-validation example

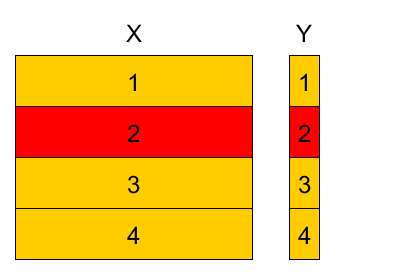
4-fold cross-validation example

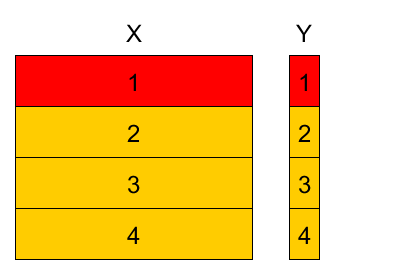
4-fold cross-validation example

  • Denote
    • $k(n)$ - fold to which observation $(\mathbf{x}_{n},y_{n})$ belongs $n\in I_{k}$.
    • $\widehat{\theta}^{-k}$ - parameter estimation using observations from all folds except fold $k$.

Cross-validation empirical risk estimation

$$\widehat{L}_{total}=\frac{1}{N}\sum_{n=1}^{N}\mathcal{L}(f_{\widehat{\theta}^{-k(n)}}(x_{n}),\,y_{n})$$

  • For $K$-fold CV we have:

    • $K$ parameters $\widehat{\theta}^{-1},...\widehat{\theta}^{-K}$
    • $K$ models $f_{\widehat{\theta}^{-1}}(\mathbf{x}),...f_{\widehat{\theta}^{-K}}(\mathbf{x}).$

    • $K$ estimations of empirical risk: $\widehat{L}_{k}=\frac{1}{\left|I_{k}\right|}\sum_{n\in I_{k}}\mathcal{L}(f_{\widehat{\theta}^{-k}}(\mathbf{x}_{n}),\,y_{n}),\,k=1,2,...K.$

      • can estimate variance & use statistics!

Comments on cross-validation

  • When number of folds $K$ is equal to number of objects $N$, this is called leave-one-out method.
  • Cross-validation uses the i.i.d.(independent and identically distributed) property of observations
  • Stratification by target $y$ helps for imbalanced/rare classes.

A/B testing

A/B testing

  • Observe test set after the models were built.
  • A/B testing procedure:
    1. divide test objects randomly into two groups - A and B.
    2. apply base model to A
    3. apply modified model to B
    4. compare final results\pause

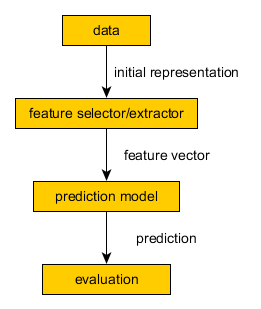
Modelling Pipelines

General Modelling Pipeline

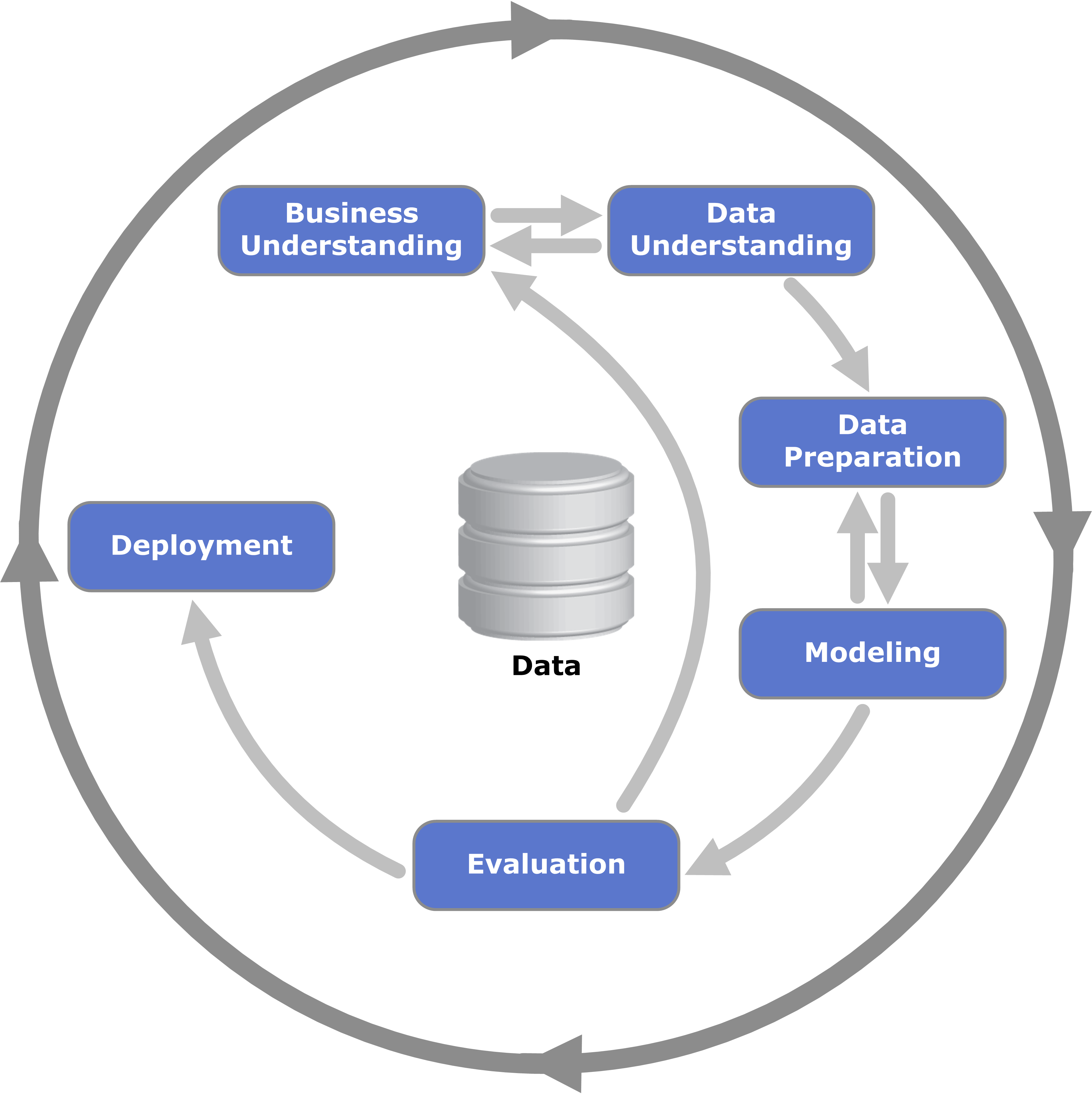
If evaluation gives poor results we may return to each of preceding stages.

CRISP DM

Summary

  • Machine learning algorithms reconstruct relationship between features $x$ and outputs $y$.
  • Relationship is reconstructed by optimal function $\widehat{y}=f_{\widehat{\theta}}(x)$ from function class $\{f_{\theta}(x),\,\theta\in\Theta\}$.
  • $\theta$ is particular controls model complexity, models may be too simple and too complex.
  • $\widehat{\theta}$ selected to minimize empirical risk $\frac{1}{N}\sum_{n=1}^{N}\mathcal{L}(f_{\theta}(x_{n}),y_{n})$ for some loss function $\mathcal{L}(\widehat{y},y)$.
  • Overfitting - non-realistic estimate of expected loss on the training set.
  • To avoid overfitting - use validation sets, cross-validation, A/B test.

FYI