Data Analysis

Andrey Shestakov (avshestakov@hse.ru)

Metric-based models1

Nearest Centroid, K-NN

1. Some materials are taken from machine learning course of Victor Kitov

Let's recall previous lecture and finish it

  • We have unsupervised and supervised learning
  • Supervised algorithms reconstruct relationship between features $x$ and outputs $y$ given in known set
  • Relationship is reconstructed by optimal function $\widehat{y}=f_{\widehat{\theta}}(x)$ from function class $\{f_{\theta}(x),\,\theta\in\Theta\}$
    • Learning = Representation + Evaluation + Optimization
  • Concepts of loss-functions and quality measures

Loss function $\mathcal{L}(\widehat{y},y)$

  • regression:
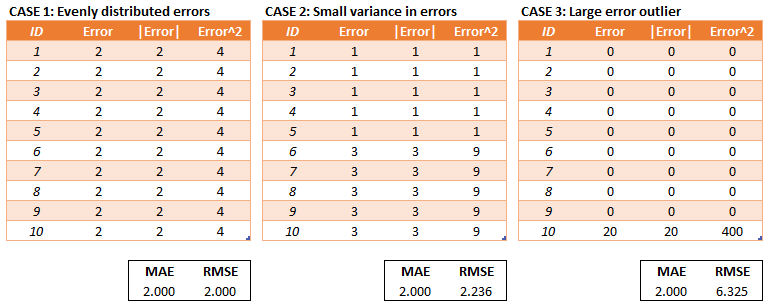
    • MAE (mean absolute error): $$ \mathcal{L}(\widehat{y},y)=\frac{1}{N}\sum\limits_i\left|\widehat{y}_i-y_i\right| $$
    • MSE (mean squared error): $$ \mathcal{L}(\widehat{y},y)=\frac{1}{N}\sum\limits_i\left(\widehat{y}_i-y_i\right)^{2} $$
  • classification:
    • log-loss $$ \mathcal{L}(\widehat{y},y)=\mathbb{I}[y==1]\log\left(p(\hat{y} = 1)\right) + \mathbb{I}[y==-1]\log\left(p(\hat{y}=-1)\right) $$
In [4]:
plt.plot(h, L1, label='logloss if y = +1')
plt.plot(h, L2, label='logloss if y = -1')
plt.ylabel('logloss')
plt.xlabel('classifier probability of +1')

_ = plt.legend()

Optimization

How to tune $f$?

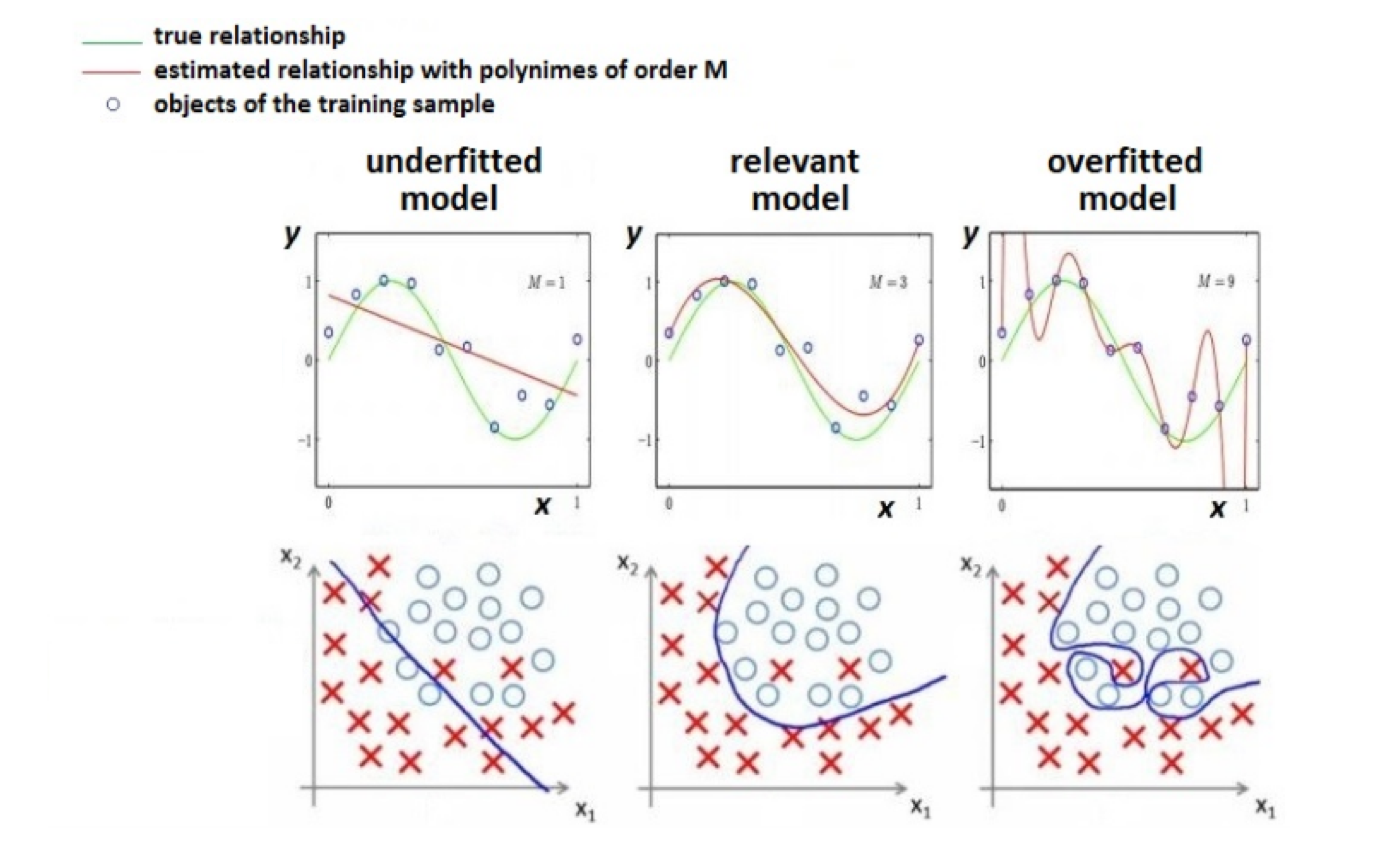
Overfitting - Underfitting

  • Theoretically, a very complex model can achive perfect quality on training dataset
  • Profit???
  • Nope...

Overfitting - Underfitting

Empirical risk

  • Want to minimize expected risk: $$ \mathit{\int}\int\mathit{\mathcal{L}(f_{\theta}(\mathbf{x}),y) \cdot p(\mathbf{x},y)d\mathbf{x}dy\to\min_{\theta}} $$

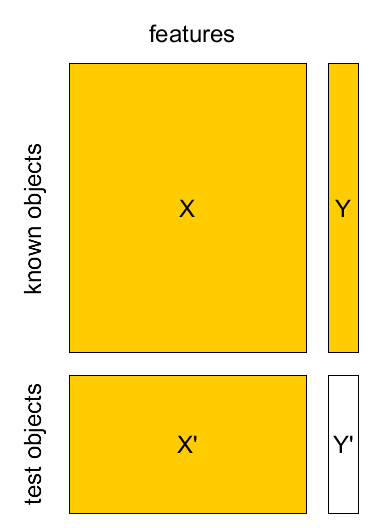
  • In fact we have only $X$,$Y$ (Known set) and $X'$ (Test set)

  • Can minimize empirical risk $$ L(\theta|X,Y)=\frac{1}{N}\sum_{n=1}^{N}\mathcal{L}(f_{\theta}(\mathbf{x}_{n}),\,y_{n}) $$

  • Method of empirical risk minimization: $$ \widehat{\theta}=\arg\min_{\theta}L(\theta|X,Y) $$

  • How to get realistic estimate of $L(\widehat{\theta}|X',Y')$?
    • separate validation set
    • cross-validation
    • A/B test

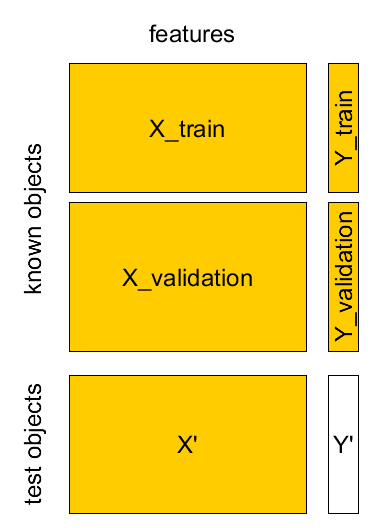
Separate validation set

  • Known sample $X,Y$: $(\mathbf{x}_{1},y_{1}),...(\mathbf{x}_{M},y_{M})$
  • Test sample $X',Y'$: $(\mathbf{x}_{1}',y_{1}'),...(\mathbf{x}_{K}',y_{K}')$

Separate validation set

Divide known set randomly or randomly with stratification:

Cross-validation

4-fold cross-validation example

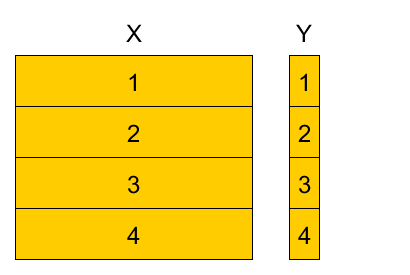
Divide training set into K parts, referred as folds (here $K=4$).

Variants:

  • randomly
  • randomly with stratification (w.r.t target value or feature value)
  • randomly with respect to time domain
  • etc

4-fold cross-validation example

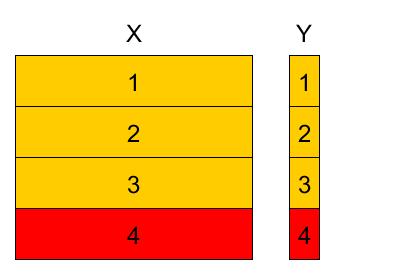
Use folds 1,2,3 for model estimation and fold 4 for model evaluation.

4-fold cross-validation example

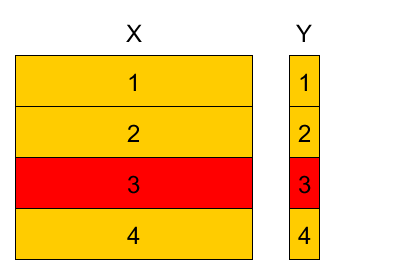
4-fold cross-validation example

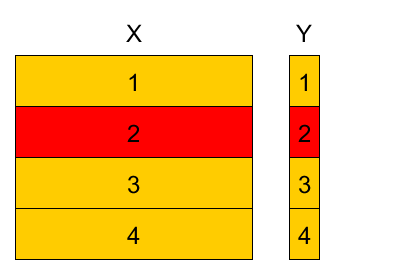
4-fold cross-validation example

4-fold cross-validation example

  • Denote
    • $k(n)$ - fold to which observation $(\mathbf{x}_{n},y_{n})$ belongs $n\in I_{k}$.
    • $\widehat{\theta}^{-k}$ - parameter estimation using observations from all folds except fold $k$.

Cross-validation empirical risk estimation

$$\widehat{L}_{total}=\frac{1}{N}\sum_{n=1}^{N}\mathcal{L}(f_{\widehat{\theta}^{-k(n)}}(x_{n}),\,y_{n})$$

  • For $K$-fold CV we have:

    • $K$ parameters $\widehat{\theta}^{-1},...\widehat{\theta}^{-K}$
    • $K$ models $f_{\widehat{\theta}^{-1}}(\mathbf{x}),...f_{\widehat{\theta}^{-K}}(\mathbf{x}).$

    • $K$ estimations of empirical risk: $\widehat{L}_{k}=\frac{1}{\left|I_{k}\right|}\sum_{n\in I_{k}}\mathcal{L}(f_{\widehat{\theta}^{-k}}(\mathbf{x}_{n}),\,y_{n}),\,k=1,2,...K.$

      • can estimate variance & use statistics!

Comments on cross-validation

  • When number of folds $K$ is equal to number of objects $N$, this is called leave-one-out method.
  • Cross-validation uses the i.i.d.(independent and identically distributed) property of observations
  • Stratification by target $y$ helps for imbalanced/rare classes.

A/B testing

A/B testing

  • Observe test set after the models were built.
  • A/B testing procedure:
    1. divide test objects randomly into two groups - A and B.
    2. apply base model to A
    3. apply modified model to B
    4. compare final results

Metric-based models

Cluster hypothesis (Compactness hypothesis)

  • the more $x$'s features are similar to ones of $x_i$'s, the more likely $\hat{y}=y_i$

Cluster hypothesis examples

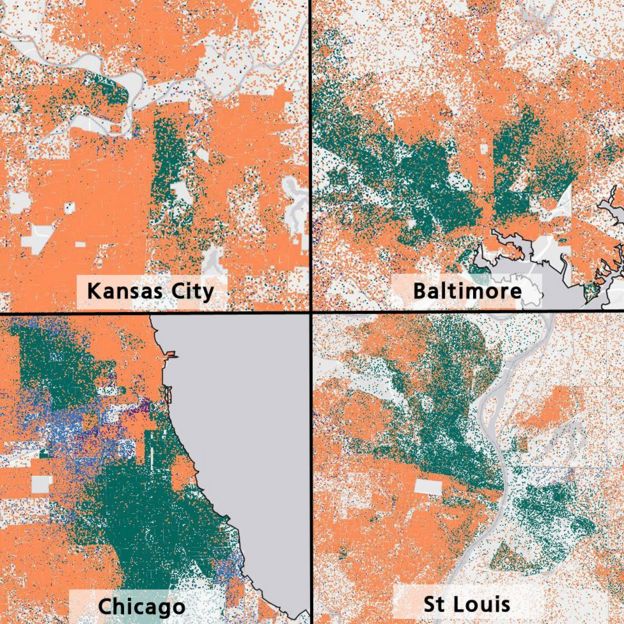
  • Objects: Families, households
  • Featuers: address, zip code, nearest marketplace... $\rightarrow$ geo-coordinates (lat, lon)
  • Target feature: race (classification)

Cluster hypothesis examples

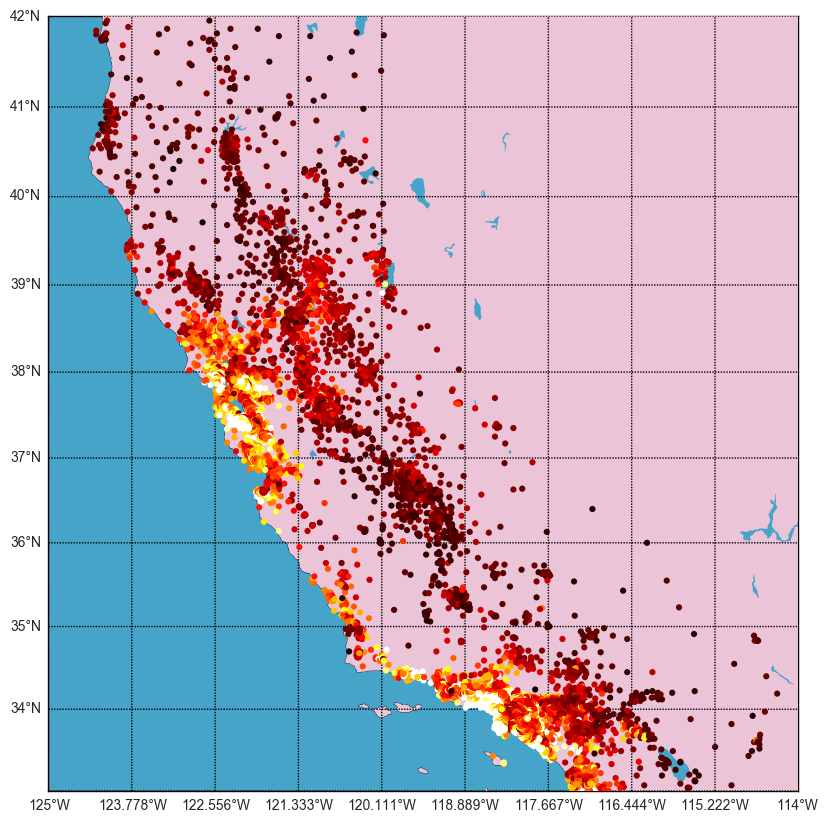
  • Objects: Houses
  • Features: address... $\rightarrow$ geo-coordinates (lat, lon)
  • Target feature: house price (regression)
  • Objects: DNA strings
  • Features: ??
  • Target features: Gene function (classification)

  • Objects: Documents, texts, articles
  • Features: Word counts
  • Target: Document category (classification)

Similarity (distance) measures

Similarity measures

  • How do we find similar objects?
  • Utilize some similiarity measure (could be metric)
$$ \rho(x_i, x_j) = \sqrt{\sum\limits_{d=1}^{D}(x^d_i - x^d_j)^2} \text{: euclidean distance} $$$$ \rho(x_i, x_j) = \sum\limits_{d=1}^{D}|x^d_i - x^d_j| \text{: manhattan distance} $$$$ \rho(x_i, x_j) = 1 - \frac{\langle x_i,x_j \rangle}{||x_i||_2\cdot||x_j||_2} \text{: cosine distance} $$

Illustration

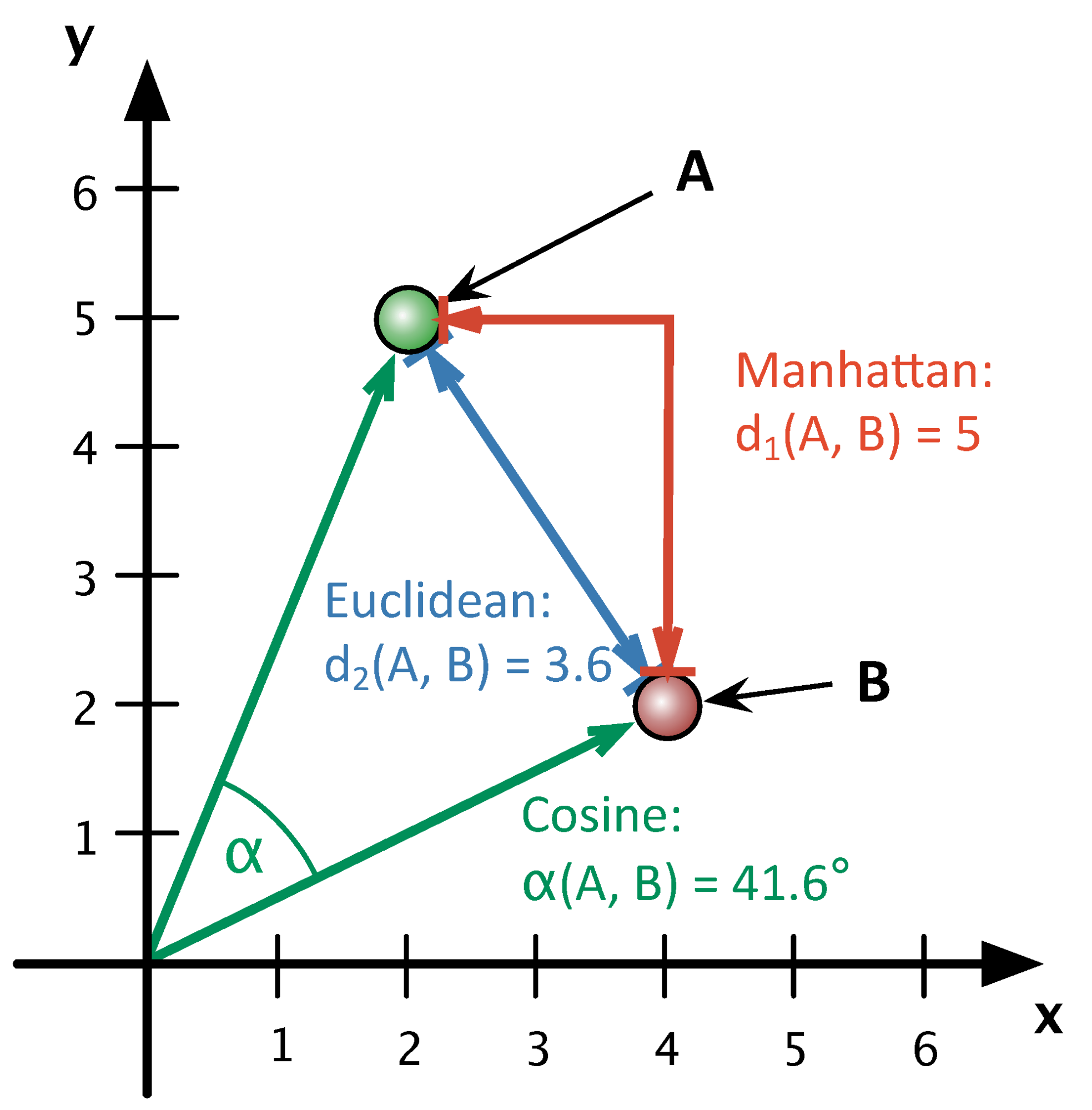
String Similarity

  • Edit distance
    • Number of insertions, replacements and deletions required to modify string $S_1$ to string $S_2$
  • Denote $D( i , j )$ as edit distance between substrings $S_1[:i]$ and $S_2[:j]$.
  • Use dynamic programming approach to compute $\rho(S_1, S_2):$
\begin{equation} D ( i , j ) = \begin{cases} {\begin{array}{llcl}0,&&&i=0,\ j=0\\i,&&&j=0,\ i>0\\j,&&&i=0,\ j>0\\\min\{\\&D(i,j-1)+1,\\&D(i-1,j)+1,&&j>0,\ i>0\\&D(i-1,j-1)+{\rm {m}}(S_{1}[i],S_{2}[j])\\\}\end{array}}, \end{cases} \end{equation}

where $m(a,b) = 0$, if $a = b$ and $1$ otherwise

Edit distance example

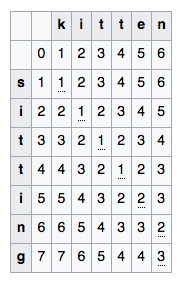
Similarity between sets

  • Suppose thet objects are represented with sets
    • Client $a$: {french fries, big-mac, coffe, muffin}
    • Client $b$: {french fries, cheese sause, cheeseburger, coffe, cherry pie}
  • Jaccard distance: $$\rho(a,b) = 1 - \frac{|a \cap b|}{|a \cup b|}$$

Nearest Centroid

Nearest centroids algorithm

  • Consider training sample $\left(x_{1},y_{1}\right),...\left(x_{N},y_{N}\right)$ with

    • $N_{1}$ representatives of 1st class
    • $N_{2}$ representatives of 2nd class
    • etc.

  • Training: Calculate centroids for each class $c=1,2,...C:$ $$ \mu_{c}=\frac{1}{N_{1}}\sum_{n=1}^{N}x_{n}\mathbb{I}[y_{n}=c] $$

  • Classification:

    • For object $x$ find the most closest centroid: $$ c=\arg\min_{i}\rho(x,\mu_{i}) $$
    • Associate $x$ the class of the most close centroid: $$ \widehat{y}(x)=c $$

Decision boundaries for 4-class nearest centroids}

In [7]:
interact(plot_centroid_class)
Out[7]:
<function __main__.plot_centroid_class()>

Questions

  • To make a decision in classification we calculate discriminant functions
    • measure score for each class: $$ c=\arg\min_{i}g_c \text{ or } c=\arg\max_{i}g_c$$
  • What are discriminant functions $g_{c}(x)$ for nearest centroid algorithm?
  • What is the complexity for:
    • training?
    • prediction?
  • What would be the shape of class separating boundary?
  • Can we use similar ideas for regression?
  • Is it always possible to have centroids?

K-nearest neighbours (KNN)

K-nearest neighbours algorithm

Classification:

  • Find $k$ closest objects to the predicted object $x$ in the training~set.
  • Associate $x$ the most frequent class among its $k$ neighbours.
In [10]:
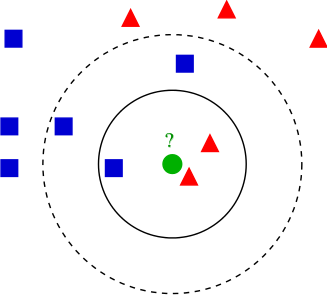
plt.scatter(X_moons[:,0], X_moons[:,1], c=y_moons, cmap=plt.cm.Spectral)
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
Out[10]:
Text(0, 0.5, '$x_2$')
In [12]:
interact(plot_knn_class, k=IntSlider(min=1, max=10, value=1))
Out[12]:
<function __main__.plot_knn_class(k=1, prob=False)>

K-nearest neighbours algorithm

Regression:

  • Find $k$ closest objects to the predicted object $x$ in the training~set.
  • Associate $x$ average output of its $k$ neighbours.
In [14]:
plt.plot(x_true, y_true, c='g', label='$f(x)$')
plt.scatter(x, y, label='actual data')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=2)
Out[14]:
<matplotlib.legend.Legend at 0x1a1dfa8da0>
In [16]:
plot_linreg()
In [18]:
interact(plot_knn, k=IntSlider(min=1, max=10, value=1))
Out[18]:
<function __main__.plot_knn(k=1)>

Comments

  • K nearest neighbours algorithm is abbreviated as K-NN.
  • $k=1$: nearest neighbour algorithm
  • what is simpler - to train K-NN model or to apply it?

Dealing with similar rank

When several classes get the same rank, we can assign to class:

  • with higher prior probability
  • having closest representative
  • having closest mean of representatives (among nearest neighbours)
  • which is more compact, having nearest most distant representative

Parameters and modifications

  • Parameters:
* None
  • Hyperparameters
    • the number of nearest neighbours $K$
    • distance metric $\rho(x,x')$

Properties

  • Advantages:

    • only similarity between objects is needed, not exact feature values.
      • so it may be applied to objects with arbitrary complex feature description
    • simple to implement
    • interpretable (kind of.. case based reasoning)
    • does not need training
      • may be applied in online scenarios
      • cross-validation may be replaced with LOO.
  • Disadvantages:
    • slow classification with complexity $O(NDK)$
    • accuracy deteriorates with the increase of feature space dimensionality (curse of dimentionality)

Special properties

Normalization of features

  • Feature scaling affects predictions of K-NN?

Normalization of features

  • Feature scaling affects predictions of K-NN?
    • sure it does! Need to normalize
  • Equal scaling - equal impact of features
  • Non-equal scaling - non-equal impact of features
  • Typical normalizations:
    • z-scoring (autoscaling): $$x_{j}'=\frac{x_{j}-\mu_{j}}{\sigma_{j}}$$
    • range scaling: $$x_{j}'=\frac{x_{j}-L_{j}}{U_{j}-L_{j}}$$

where $\mu_{j},\,\sigma_{j},\,L_{j},\,U_{j}$ are mean value, standard deviation, minimum and maximum value of the $j$-th feature.

The curse of dimensionality

  • Phenomenon that occures in various fields and have varoius consequences (mainly negative)
  • The curse of dimensionality: with growing $D$ data distribution becomes sparse and insufficient.

The curse of dimensionality

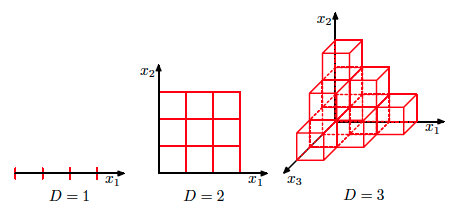
  • At what rate should training size grow with increase of $D$ to compensate curse of dimensionality?

The curse of dimensionality

$D=2$ $D=2 \dots 100$
$$ \lim_{D \rightarrow \infty} \frac{\text{dist}_{max} - \text{dist}_{min}}{\text{dist}_{min}} = 0$$

Curse of dimensionality

  • Case of K-nearest neighbours:
    • assumption: objects are distributed uniformly in unit feature space
    • ball of radius $R$ has volume $V(R)=CR^{D}$, where $C=\frac{\pi^{D/2}}{\Gamma(D/2+1)}$.
    • ratio of volumes of unit cube and included ball: $$ \frac{V(0.5)}{1}=\frac{0.5^{D}\pi^{D/2}}{(D/2)!}\stackrel{D\to\infty}{\longrightarrow}0 $$
    • most of volume concentrates on the corners of the cube
    • nearest neighbours stop being close by distance
  • Good news: in real tasks the true dimensionality of the data is often less than $D$ and objects belong to the manifold with smaller dimensionality.

Weighted account

Equal voting

  • Consider for object $x$:

    • $x_{i_{1}}$most close neigbour, $x_{i_{2}}$ - second most close neighbour, etc. $$ \rho(x,x_{i_{1}})\le\rho(x,x_{i_{2}})\le...\le\rho(x,x_{i_{N}}) $$

  • Classification: $$\begin{align*} g_{c}(x) & =\sum_{k=1}^{K}\mathbb{I}[y_{i_{k}}=c],\quad c=1,2,...C.\\ \widehat{y}(x) & =\arg\max_{c}g_{c}(x) \end{align*} $$

  • Regression: $$ \widehat{y}(x)=\frac{1}{K}\sum_{k=1}^{K}y_{i_{k}} $$

Weighted voting

  • Weighted classification: $$\begin{align*} g_{c}(x) & =\sum_{k=1}^{K}w(k,\,\rho(x,x_{i_{k}}))\mathbb{I}[y_{i_{k}}=c],\quad c=1,2,...C.\\ \widehat{y}(x) & =\arg\max_{c}g_{c}(x) \end{align*} $$

  • Weighted regression: $$ \widehat{y}(x)=\frac{\sum_{k=1}^{K}w(k,\,\rho(x,x_{i_{k}}))y_{i_{k}}}{\sum_{k=1}^{K}w(k,\,\rho(x,x_{i_{k}}))} $$

Commonly chosen weights

Index dependent weights: $$ w_{k}=\alpha^{k},\quad\alpha\in(0,1) $$ $$ w_{k}=\frac{K+1-k}{K} $$

Distance dependent weights:

$$ w_{k}=\begin{cases} \frac{\rho(z_{K},x)-\rho(z_{k},x)}{\rho(z_{K},x)-\rho(z_{1},x)}, & \rho(z_{K},x)\ne\rho(z_{1},x)\\ 1 & \rho(z_{K},x)=\rho(z_{1},x) \end{cases} $$$$ w_{k}=\frac{1}{\rho(z_{k},x)} $$

Kernels

  • $K(\rho, h)$ - some decreasing function
  • $h \geq 0$ - parameter (window width)
  • gaussian kernel $$K(\rho, h) \propto \exp(- \frac{\rho(x, x')^2}{2h^2})$$
  • tophat kernel $$K(\rho, h) \propto 1\ if\ x < h$$
  • epanechnikov kernel $$K(\rho, h) \propto 1 - \frac{\rho(x, x')^2}{h^2}$$
  • exponential kernel $$K(\rho, h) \propto \exp(-\rho(x, x')/h)$$
  • linear kernel $$K(\rho, h) \propto 1 - \rho(x, x')/h\ if\ d < h$$

Kernels

In [20]:
interact(plot_knn_class_kernel, k=IntSlider(min=1, max=10, value=1), 
               h=FloatSlider(min=0.05, max=5, value=1, step=0.05))
Out[20]:
<function __main__.plot_knn_class_kernel(k=1, h=0.5, prob=False, use_all=False)>

Summary

  • Important hyperparameters of K-NN:

    • $K$: controls model complexity
    • $\rho(x,x')$

  • Output depends on feature scaling.

    • scaling to equal / non-equal scatter possible.
  • Prone to curse of dimensionality.
  • Fast training but long prediction.
    • some efficiency improvements are possible though
  • Weighted account for objects possible.

FYI

Use Case

  • Despite being very primitive KNN demonstrated good performance in Facebook's Kaggle competiton
  • Used to make features
  • Competiton page