Data Analysis
Andrey Shestakov (avshestakov@hse.ru)
Feature Selection and Dimention Reduction. PCA.1
1. Some materials are taken from machine learning course of Victor Kitov
Feature Selection vs. Dimension Reduction¶
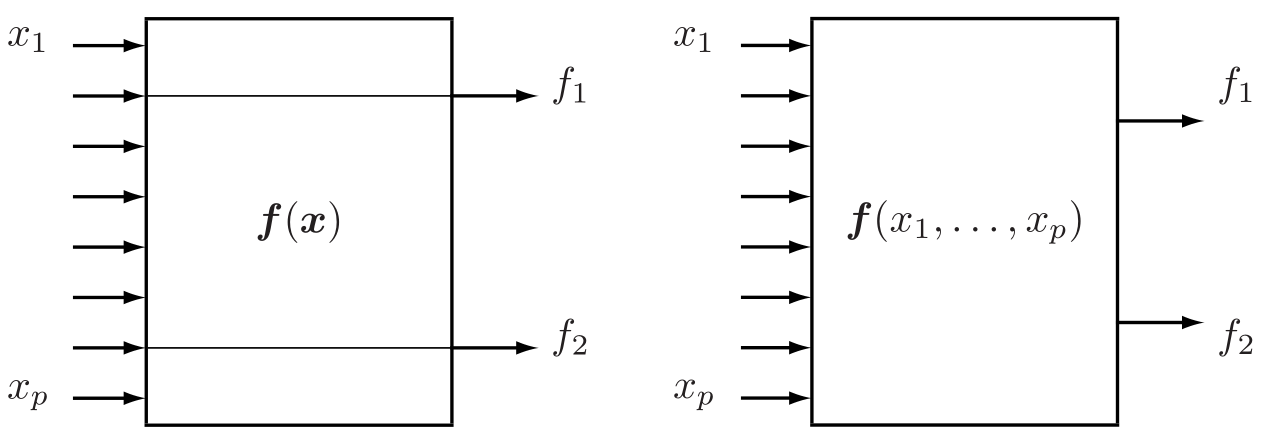
- Feature selection is a process of selecting a subset of original features with minimum loss of information related to final task (classification, regression, etc.)
- Dimension reduction is a result of some transformation of initial features to (possibly) lower dimension feature space
Why feature selection?¶
- increase predictive accuracy of classifier
- improve optimization stability by removing multicollinearity
- increase computational efficiency
- reduce cost of future data collection
- make classifier more interpretable
Not always necessary step
- some methods have implicit feature selection
Feature Selection Approaches¶
- Unsupervised methods
- don't use target feature
- Filter methdos
- use target feature
- consider each feature independently
- Wrapper methods
- uses model quality
- Embedded methdos
- embedded inside model
"Unsupervised" methods¶
- Determine feature importance regardless of target feature
- Your ideas?
Filter methods¶
- Features are considered independently of each other
- Individual predictive power is measures
Basically
- Order features with respect to feature importances $I(f)$: $$ I(f_{1})> I(f_{2})> \dots\ge I(f_{D}) $$
- Select top $m$ $$ \hat{F}=\{f_{1},f_{2},...f_{m}\} $$
- Simple to implement
- Usually quite fast
- When features are correlated, it will take many redundant features
Examples¶
- Correlation
- Which kind of relationship does correlation measure?
- Mutual Information
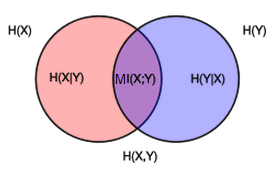
- Entropy of variable $Y$: $H(Y) = - \sum_y p(y)\ln p(y)$
- Conditional entropy of $Y$ after observing $X$: $H(y|x) = - \sum_x p(x) \sum_y p(y|x)\ln p(y|x) $
- Mutial information: $$MI(Y, X) = \sum_{x,y} p(x,y) \ln\left[\frac{p(x,y)}{p(x)p(y)}\right]$$
- Mutual information measures how much $X$ and $Y$ share information between each other
- $MI(Y,X) = H(Y) - H(Y|X)$
df_titanic = pd.read_csv('data/titanic.csv')
df_titanic.head()
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
P = pd.crosstab(df_titanic.Survived, df_titanic.Sex, normalize=True).values
print(P)
[[0.09090909 0.52525253] [0.26150393 0.12233446]]
px = P.sum(axis=1)[:, np.newaxis]
py = P.sum(axis=0)[:, np.newaxis]
print(px)
print(py)
[[0.61616162] [0.38383838]] [[0.35241302] [0.64758698]]
px.dot(py.T)
array([[0.21714338, 0.39901824],
[0.13526964, 0.24856874]])
mutual_info(df_titanic.Pclass, df_titanic.Survived)
0.05810725269032348
Wrapper methods¶
- Selecting suboptimal subset of features
- Could be slow
- Examples:
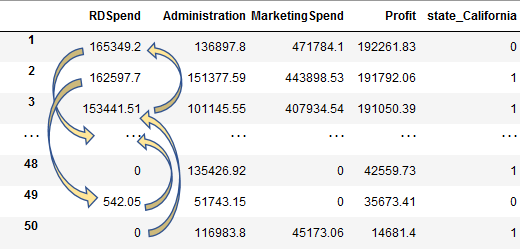
- Recursive Feature Elimination
- Consider full set of features
- Fit a model, measure feature importance (based on model)
- Remove least important feature(s)
- Repeat
- Boruta Algorithm
- Recursive Feature Elimination
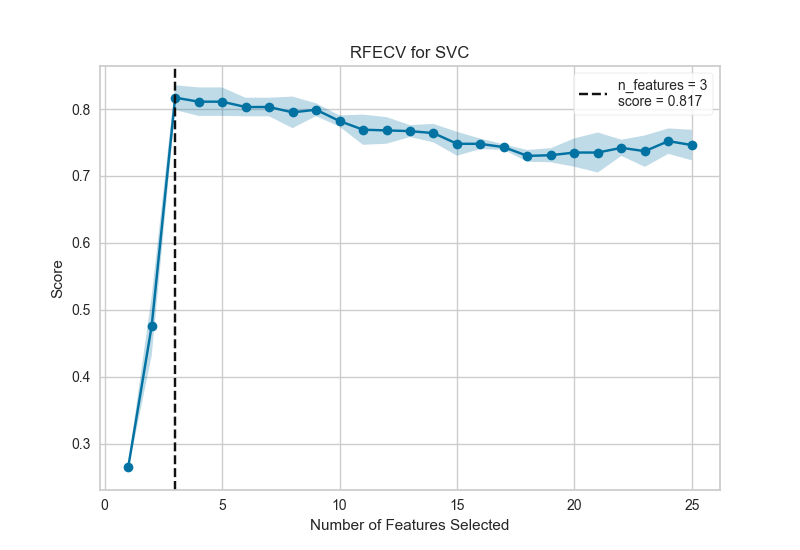
Embedded methods¶
- Feature selection process in included in the model
- Examples:
- Decision Trees
- Linear model with L1 regularization
Something different: permutation importance¶
- Train your model
- Calculate quality measure on validation set
- For each feature:
- replace given values with random values from the same distribution
- ... or perform random shuffling
- observe the difference in quality measure
Feature Selection vs. Feature Extraction¶

iris = sns.load_dataset('iris')
sns.pairplot(iris, hue='species')
<seaborn.axisgrid.PairGrid at 0x7fada055da20>
# Перейдем от 4 признаков к 2 компонентам
pca = PCA(n_components=2, random_state=123)
pca.fit(X) # Никакого "y"
PC = pca.transform(X)
plt.scatter(PC[:,0], PC[:,1],c=y)
<matplotlib.collections.PathCollection at 0x7fad98296208>

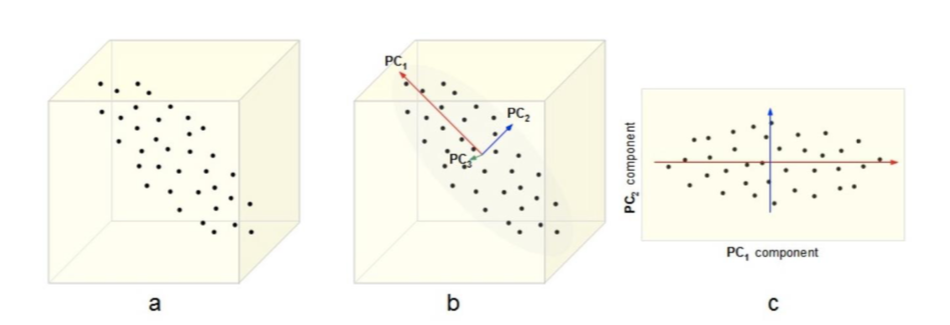
PCA¶
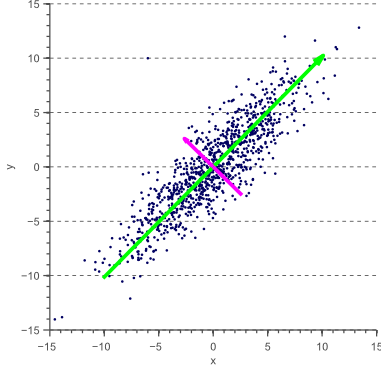
- Intuition 2: Find a subspace $L$ (of lesser dimention) s.t. the sum of squares of differences between points and their projections is minimized
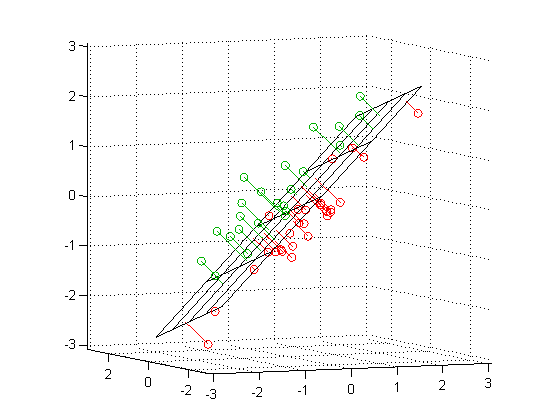
PCA¶
- Intuition 2: Find a subspace $L$ (of lesser dimention) s.t. the sum of squares of differences between points and their projections is minimized
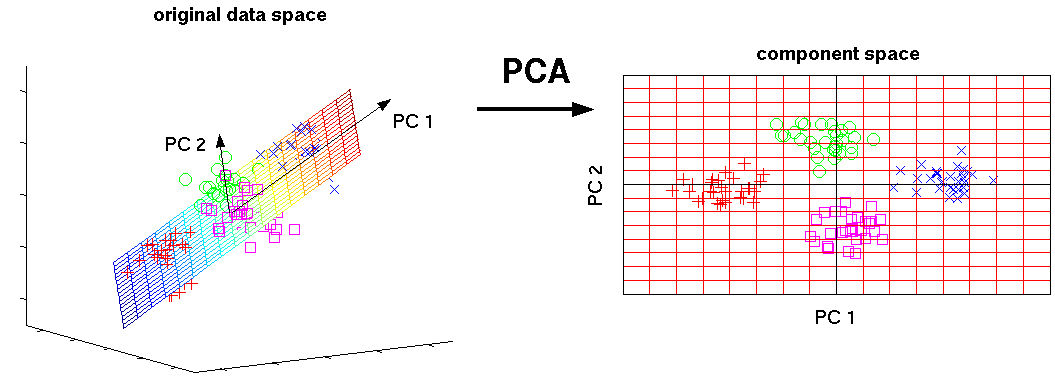
In other words, we can consider PCA as¶
- A transformation of your inital feature axes ...
- New axes are just a linear combination of initial axes
- New axes are orthogonal (orthonormal) to each other
- Variance of data across those axes is maximized
- ... which keeps only the most "informative" axes
How do we project data on new axes?¶
- Consider an object $x$ with 3 features: $x=(-0.343, -0.754, 0.241)$
- We can say that it is spanned on 3 basis vectors of our feature space: $$ e_1 = \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right) \quad e_2 = \left( \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right) \quad e_3 = \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) \quad$$
- Consider new basis vectors:
- How do we project $x$ on it?
Projecting¶
$$ a_1 = \left( \begin{array}{c} -0.390 \\ 0.089 \\ -0.916 \end{array} \right) \quad a_2 = \left( \begin{array}{c} -0.639 \\ -0.742 \\ 0.200 \end{array} \right) \quad a_3 = \left( \begin{array}{c} -0.663 \\ 0.664 \\ 0.346 \end{array} \right) \quad$$$$ z = A^\top x = \left( \begin{array}{ccc} -0.390 & 0.089 & -0.916\\ -0.639 & -0.742 & 0.200 \\ -0.663 & 0.664 & 0.346 \end{array} \right) \left( \begin{array}{c} -0.343 \\ -0.754 \\ 0.241 \end{array} \right) = \left( \begin{array}{c} -1.154 \\ 0.828 \\ 0.190 \end{array} \right)$$That is: $$ z = -1.154 a_1 + 0.828 a_2 + 0.190 a_3$$
(Example from Mohammed J. Zaki, Ch7 )
- So how do we find those $a_i$?
- Orthonormality
- Maximize variance
- Vectors $a_i$ are called principal components
Construction of PCA¶
Construction of PCA¶
- Principal components $a_{1},a_{2},...a_{D}\in\mathbb{R}^{D}$ are orthonormal: $$\langle a_{i},a_{j}\rangle=\begin{cases} 1, & i=j\\ 0 & i\ne j \end{cases}$$
- Maximize variance
- Datapoints in $X$ assumed to be centered (and scaled)
- $z_i = a^\top x_i$ - projection of $x_i$ on $a$
- Variance across principal component $a$ for dataset $$ \begin{align} \sigma^2_a & = \frac{1}{n}\sum\limits_{i=1}^n(z_i - \mu_z)^2 \\ & = \frac{1}{n}\sum\limits_{i=1}^n(a^\top x_i)^2 \\ & = \frac{1}{n}\sum\limits_{i=1}^n a^\top( x_i x_i^\top) a \\ & = a^\top \left(\frac{1}{n}\sum\limits_{i=1}^n x_i x_i^\top \right) a \\ & = a^\top X^\top X a \\ & = a^\top C a \rightarrow \max_a \\ \end{align} $$
- $C = X^\top X$ - convariance (correlation in case of scaled dataset) matrix
Covariance matrix reminder¶
- Given $N$ observations of variables $x$ and $y$, covariace is calculated as $${s}_{xy}=\mathrm {cov} (x,y)={1 \over N}\sum _{n=1}^{N}\left(x_{n}-{\overline {x}}\right)\left(y_{n}-{\overline {y}}\right)$$
- scaled measure of linear dependency between $x$ and $y$
Relationship with variance and correlation:
$\mathrm {cov} (x,x) = \mathrm {var} (x)$
$\mathrm {corr} (x,y)=\frac{\mathrm {cov} (x,y)}{\mathrm {var} (x)\mathrm {var} (y)}$
Covariance matrix reminder¶
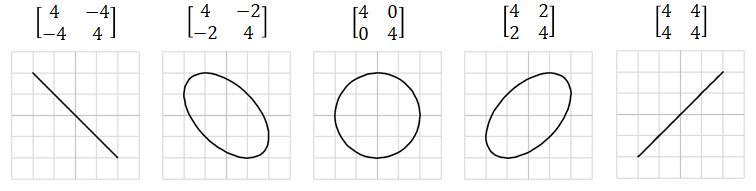
- If $X$ is feature matrix (features are on columns) we can calculate covariance matrix: $$\operatorname {cov} (X ) ={\begin{bmatrix}\mathrm {var}(x_1)&\mathrm {cov} (x_1,x_2)&\cdots &\mathrm {cov} (x_1,x_d)\\\\\mathrm {cov} (x_2,x_1)&\mathrm {var}(x_2)&\cdots &\mathrm {cov} (x_2,x_d)\\\\\vdots &\vdots &\ddots &\vdots \\\\\mathrm {cov} (x_d,x_1)&\mathrm {cov} (x_d,x_2)&\cdots &\mathrm {var}(x_d)\end{bmatrix}}$$
Examples of data distributions and corresponding covariances
Useful properties of $X^\top X$¶
- $X^\top X$ - symmetric and positive semi-definite
- $(X^\top X)^\top = X^\top X$
- $\forall w \in \mathbb{R}^D:\ w^\top (X^\top X) w \geq 0$
- Properties
- All eigenvalues $\lambda_i \in \mathbb{R}, \lambda_i \geq 0$ (we also assume $\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_d $)
- Eigenvectors for $\lambda_i \neq \lambda_j $ are orthogonal: $v_i^\top v_j = 0$
- For each unique eigenvalue $\lambda_i$ there is a unique $v_i$
Construction of PCA¶
- $a_{1}$ is selected to maximize $a_1^\top X^\top X a_1$ subject to $\langle a_{1},a_{1}\rangle=1$
- $a_{2}$ is selected to maximize $a_2^\top X^\top X a_2$ subject to $\langle a_{2},a_{2}\rangle=1$, $\langle a_{2},a_{1}\rangle=0$
- $a_{3}$ is selected to maximize $a_3^\top X^\top X a_3$ subject to $\langle a_{3},a_{3}\rangle=1$, $\langle a_{3},a_{1}\rangle=\langle a_{3},a_{2}\rangle=0$
etc.
Derivation of 1st component¶
$$ \begin{equation} \begin{cases} a_1^\top X^\top X a_1 \rightarrow \max_{a_1} \\ a_1^\top a_1 = 1 \end{cases} \end{equation} $$- Lagrangian of optimization problem $$ \mathcal{L}(a_1, \nu) = a_1^\top X^\top X a_1 - \nu (a_1^\top a_1 - 1) \rightarrow max_{a_1, \nu}$$
- Derivative w.r.t. $a_1$ $$ \frac{\partial\mathcal{L}}{\partial a_1} = 2X^\top X a_1 - 2\nu a_1 = 0 $$
- so $a_1$ is selected from a set of eigenvectors of $X^\top X$. But which one?
Back to component 1¶
Initially, our objective was $$a_1^\top X^\top X a_1 \rightarrow \max_{a_1}$$
From lagrangian we derived that $$X^\top X a_1 = \nu a_1$$
Putting one in to another: $$ a_1^\top X^\top X a_1 = \nu a_1^\top a_1 = \nu \rightarrow \max$$
That means:
- $\nu$ should be the greatest eigenvalue of matrix $X^\top X$, which is $\lambda_1$
- $a_1$ is eigenvector, correspondent to $\lambda_1$
Derivation of 2nd component¶
$$ \begin{equation} \begin{cases} a_2^\top X^\top X a_2 \rightarrow \max_{a_2} \\ a_2^\top a_2 = 1 \\ a_2^\top a_1 = 0 \end{cases} \end{equation} $$- Lagrangian of optimization problem $$ \mathcal{L}(a_2, \nu,\alpha) = a_2^\top X^\top X a_2 - \nu (a_2^\top a_2 - 1) - \alpha (a_1^\top a_2) \rightarrow max_{a_2, \nu,\alpha}$$
- Derivative w.r.t. $a_2$ $$ \frac{\partial\mathcal{L}}{\partial a_2} = 2X^\top X a_2 - 2\nu a_2 - \alpha a_1 = 0 $$
Derivation of 2nd component¶
By multiplying by $a_1^\top$ : $$ a_1^\top\frac{\partial\mathcal{L}}{\partial a_2} = 2a_1^\top X^\top X a_2 - 2\nu a_1^\top a_2 - \alpha a_1^\top a_1 = 0 $$
It follows that $\alpha a_1^\top a_1 = \alpha = 0$, which means that $$ \frac{\partial\mathcal{L}}{\partial a_2} = 2X^\top X a_2 - \nu a_2 = 0 $$ And $a_2$ is selected from a set of eigenvectors of $X^\top X$. Again, which one?
Derivations of other components proceeds in the same manner
PCA algorithm¶
- Center (and scale) dataset
- Calculate covariance matrix $С=X^\top X$
- Find first $k$ eigenvalues and eigenvectors $$A = \left[ \begin{array}{cccc} \mid & \mid & & \mid\\ a_{1} & a_{2} & \ldots & a_{k} \\ \mid & \mid & & \mid \end{array} \right] $$
- Perform projection: $$ Z = XA $$
Explained variance or why do we neeed $\lambda$?¶
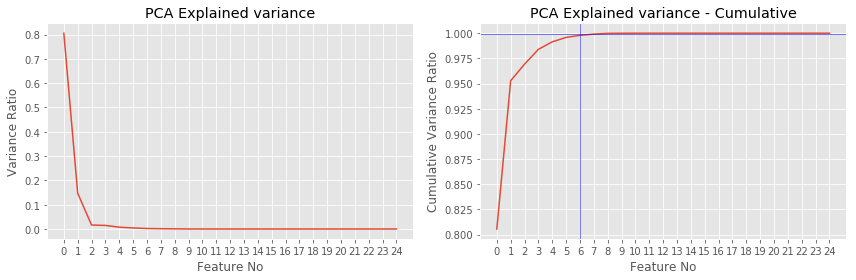
- As we remember $$a_i^\top X^\top X a_i = \lambda_i,$$ which means that $\lambda_i$ shows variance of data "explained" by $a_i$
- We can calculate explained variance ratio for $a_i$: $$ \frac{\lambda_{i}}{\sum_{d=1}^{D}\lambda_{d}} $$
(Supplementary) alternative view on PCA¶
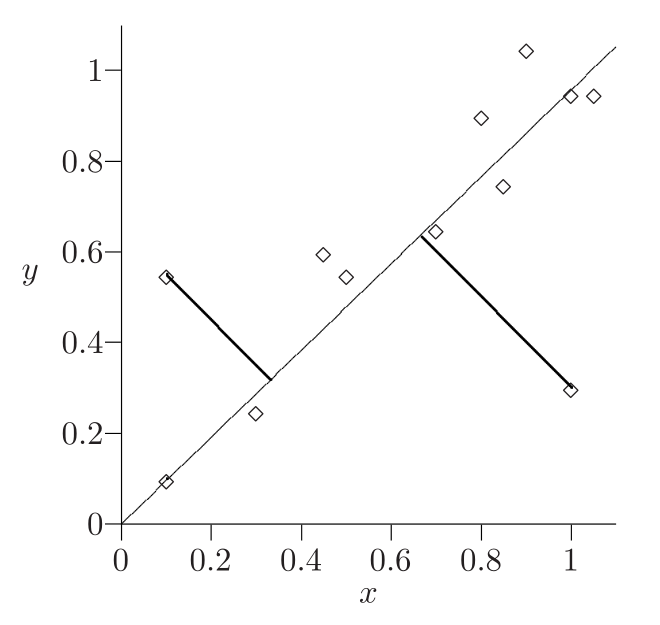
Best hyperplane fit¶
For point $x$ and subspace $L$ denote:
- $p$: the projection of $x$ on $L$
- $h$: orthogonal complement
- $x=p+h$, $\langle p,h\rangle=0$,
Proposition¶
$\|x\|^2 = \|p\|^2 + \|h\|^2$
For training set $x_{1},x_{2},...x_{N}$ and subspace $L$ we can find:
- projections: $p_{1},p_{2},...p_{N}$
- orthogonal complements: $h_{1},h_{2},...h_{N}$.
Example: plane of best fit¶

Best subspace fit¶
Definition¶
Best-fit $k$-dimentional subspace for a set of points $x_1 \dots x_N$ is a subspace, spanned by $k$ vectors $a_1$, $a_2$, $\dots$, $a_k$, solving
$$ \sum_{n=1}^N \| h_n \| ^2 \rightarrow \min\limits_{a_1, a_2,\dots,a_k}$$or
$$ \sum_{n=1}^N \| p_n \| ^2 \rightarrow \max\limits_{a_1, a_2,\dots,a_k}$$Definition of PCA¶
Principal components $a_1, a_2, \dots, a_k$ are vectors, forming orthonormal basis in the k-dimentional subspace of best fit
Properties¶
- Not invariant to translation:
- center data before PCA: $$ x\leftarrow x-\mu\text{ where }\mu=\frac{1}{N}\sum_{n=1}^{N}x_{n} $$
- Not invariant to scaling:
- scale features to have unit variance before PCA
Construction of PCA¶
Construction of PCA¶
- Datapoints in $X$ assumed to be centralized and scaled (!)
- Principal components $a_{1},a_{2},...a_{D}\in\mathbb{R}^{D}$ are found such that $\langle a_{i},a_{j}\rangle=\begin{cases} 1, & i=j\\ 0 & i\ne j \end{cases}$
- $Xa_{i}$ is a vector of projections of all objects onto the $i$-th principal component.
- For any object $x$ its projections onto principal components are equal to: $$ p=A^{T}x=[\langle a_{1},x\rangle,...\langle a_{D},x\rangle]^{T} $$ where $A=[a_{1};a_{2};...a_{D}]\in\mathbb{R}^{DxD}$.
Construction of PCA¶
- $a_{1}$ is selected to maximize $\left\lVert Xa_{1}\right\rVert $ subject to $\langle a_{1},a_{1}\rangle=1$
- $a_{2}$ is selected to maximize $\left\lVert Xa_{2}\right\rVert $ subject to $\langle a_{2},a_{2}\rangle=1$, $\langle a_{2},a_{1}\rangle=0$
- $a_{3}$ is selected to maximize $\left\lVert Xa_{3}\right\rVert $ subject to $\langle a_{3},a_{3}\rangle=1$, $\langle a_{3},a_{1}\rangle=\langle a_{3},a_{2}\rangle=0$
etc.
PCA summary¶
- Dimensionality reduction - common preprocessing step for efficiency and numerical stability.
- Solution vectors $a_1,\dots,a_k$ are called top $k$ principal components.
- Principal component analysis - expression of $x$ in terms of first $k$ principal components.
- It is unsupervised linear dimensionality reduction.
- Solution is achieved on top $k$ eigenvectors $a_{1},...a_{k}$ of covariance matrix.
References¶
- Mohammed J. Zaki - Data Mining and Analysis: Fundamental Concepts and Algorithms, Ch7
- Understanding covariance matrix
- PCA tutorial
- PCA in python - step by step