Data Analysis

Andrey Shestakov (avshestakov@hse.ru)

---

Introduction to Recommender Systems¹

^{1. Some materials are taken from machine learning course of Victor Kitov}

Motivation

• Everyday people have to make decisions:

  • what music to listen
  • what movies to see
  • what books to read
  • what food to eat
  • what games to play
  • ...

• Multitude of choices

  • Spotify - 30kk. songs
  • Netflix - 20k. movies and series
  • Amazon - 500k. books
  • Steam - 20k games

To filter out the seach people can rely on recommendations

• of their friends (if there are friends)
• of some reviews

These recommendations are too narrow and standard

• rely on information of a handful of people
• not tuned for individual user tastes

Need automatic recommendation system!

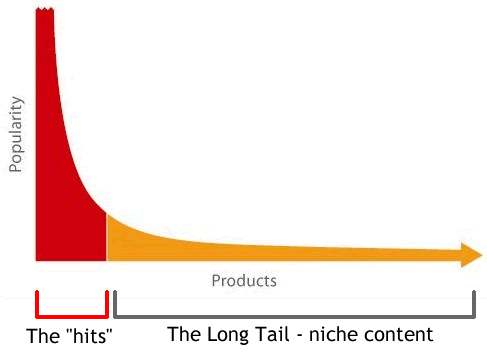
Long Tail Phenomenon

Few words on history

Netflix prize

• Competition for the best recommendation algirithm
• October 2007 - September 2009
• Prize: 1 000 000 $
• 480 000 users
• 17 770 movies
• format: [user, movie, datetime, rating]
• grades: 1,2,3,4,5
• quality measure: RMSE

Netflix Prize

Recsys

Annual international conference

Collaborative filtering

Collaborative filtering

A method of making automatic predictions about the interests of a user by collecting prefences or taste information from similar users

• Generic CF algorithm
  1. Look for users who share the same rating patterns with current user
  2. Use their ratings to predict currently unknown user ratings

• Main assumption: if person A has the same opinion as a persion B on an issue, A is more likely to have B's opinion on a different issue.
  • Have you already seen this idea?

Collaborative filtering

Challenges

• Scalability
  • many users and items
• Cold start
  • new user has not rated many items - hard to predict his preferences
  • new item was not rated by many users - hard to predict its characteristics
• Shilling attacks
  • shop representatives may give lots of positive ratings for their own items ang negative ratings for theis competitors
• Learning Loop
  • once the model have been relearned it may relearned its previous predictions - does not gain new knowledge
• Obvious recommendations

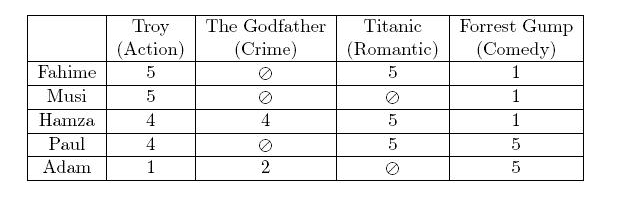
Core concepts

• Users give ratings to items

• Users give ratings to items
  • Binary
  • "Stars"
  • Implicit

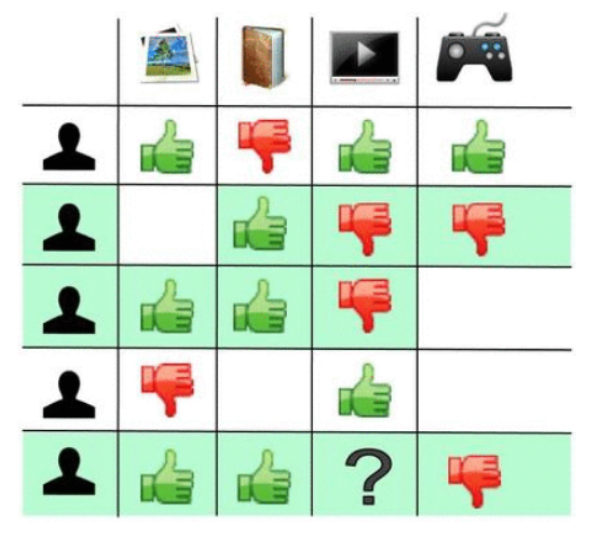
• Tasks of RecSys:
  • Fill missing values of the ratings
  • Recommend items to user
    • may not be the highest ranked!

Notations

• $U$ - set of all users
• $I$ - set of all items
• $u$, $v$ - some users
• $i$, $j$ - some items
• $U_i$ - set of users, that rated item $i$
• $I_u$ - set of items, that have been rated by user $u$
• $R_{ui}$ - actual rating of item $i$ by user $u$
• $\hat{R}_{ui}$ - predicted rating of item $i$ by user $u$

Baseline

Baseline ideas

• $b_{ui} = \mu$, $(\mu = \frac{1}{n}\sum\limits_{u,i} R_{ui})$
• $b_{ui} = \bar{R}_u = \frac{1}{|I_u|}\sum\limits_{i\in I_u} R_{ui}$
• $b_{ui} = \bar{R}_i = \frac{1}{|U_i|}\sum\limits_{u\in U_i} R_{ui}$

General baseline

• $b_{ui} = \mu + b_u + b_i$,
• $b_{u} = \frac{1}{|I_u|}\sum_{i\in I_u}(R_{ui} - \mu)$
• $b_{i} = \frac{1}{|U_i|}\sum_{u\in U_i}(R_{ui} - b_u - \mu)$

Intuition

• $b_u$ is how much higher user rates items than on average
• $b_i$ is how much item $i$ is rated higher than average user rating

General baseline

• $b_{ui} = \mu + b_u + b_i$,
• $b_{u} = \frac{1}{|I_u|+\alpha}\sum_{i\in I_u}(R_{ui} - \mu)$
• $b_{i} = \frac{1}{|U_i|+\beta}\sum_{u\in U_i}(R_{ui} - b_u - \mu)$

• What is the idea behind $\alpha$ and $\beta$?

Motivation

• Compare accuracy with advanced model
• Can compute missing values with baseline values
• Normalization: predict $R_{ui} - b_{ui}$ instead of $R_{ui}$

User-based Collaborative filteting

User-based CF

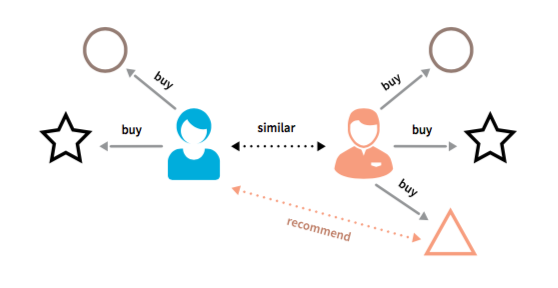
User-based CF

• Also known as K-NN CF

• Define similarity function on users: $s \in \mathbb{R}^{U \times U}$

• Algorithm with level normalization:

  1. For user $u$ find a neighbourhood of similar users $N(u)$
  2. Generate rating predictions by averaging over $N(u)$ $$ \hat{R}_{ui} = \bar{R}_u + \frac{\sum_{v \in N(u)} s_{uv}(R_{vi} - \bar{R}_v)}{\sum_{v \in N(u)} \left| s_{uv}\right|} $$

• $\bar{R}_u$ - adjustment to compensate average rating behaviour of u

  • skeptics/optimists normalization

User-based CF

• Algorithm with level and scale normalization:

  1. For user $u$ find a neighbourhood of similar users $N(u)$
  2. Generate rating predictions by averaging over $N(u)$ $$ \hat{R}_{ui} = \bar{R}_u + \sigma_u\frac{\sum_{v \in N(u)} s_{uv}(R_{vi} - \bar{R}_v)/\sigma_v}{\sum_{v \in N(u)} \left| s_{uv}\right|} $$

• where $\sigma_u$ is standard deviation of user $u$ ratings

Number of NN

• In general 20-50 is suggested
• Also possible
  • Take all
  • Top-k
  • $s_{uv} > \theta$

Similarity measures

• For each pair $(u,v)$ the intersection of rated items should be considered!

• Pearson correlation $$ s_{uv} = \frac{\sum\limits_{i \in I_u\cap I_v} (R_{ui} - \bar{R}_u)(R_{vi} - \bar{R}_v)}{\sqrt{\sum\limits_{i \in I_u\cap I_v}(R_{ui} - \bar{R}_u)^2}\sqrt{\sum\limits_{i \in I_u\cap I_v}(R_{vi} - \bar{R}_v)^2}}$$

• tends to give high similarity for users with few ratings

  • solution $s'_{uv} = s_{uv}\cdot \min\{|I_u\cap I_v|/50, 1\}$

Other possible measures

• Spearman correlation
  • correlatino between ranks of ratings
  • captures the level of monotone dependencies
• Cosine similarity $$ s_{uv} = \frac{\sum\limits_{i \in I_u\cap I_v} R_{ui} R_{vi}}{\sqrt{{\sum\limits_{i \in I_u\cap I_v}R_{ui}^2}}\sqrt{{\sum\limits_{i \in I_u\cap I_v}R_{vi}^2}}}$$

Item-based Collaborative filteting

Item-based CF

Item-based CF

• Also determine similarity function between items $s \in \mathbb{R}^{I \times I}$

• For item $i$ find a set of items similar to it and rated by user $u$: $N(i)$

• Predict $R_{ui}$ by averaging over $N(i)$ $$ \hat{R}_{ui} = \frac{\sum_{j \in N(i)} s_{ij}R_{uj}}{\sum_{j \in N(i)} \left| s_{ij}\right|} \qquad (1)$$

Similarities for Item-based CF

• Conditional probability of purchase $$ s_{ij} = \frac{n_{ij}}{n_i} $$
• Dependency $$ s_{ij} = \frac{n_{ij}}{n_i n_j} $$

Benefits of item-based CF

• We need to generate recomendations for user $u$ in real-time when he is active

• When user is active - his ratings change

  • User-based CF: after changes in rating we need to recalculate all nearest neighbours or user - long!
  • Item-based CF: for each pair of items we precalculate similarities $s_{ij}$ and find nearest neighbours of each item. Change in user ratings affects only the weights in $(1)$

• Due to possible precomputations, item-item becomes more efficient

  • user profile is more dynamic
  • item profile is more static

Latent variable models

Latent variables models

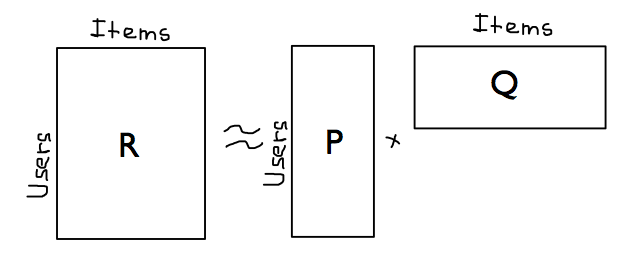
For each user $u$ build a vector $p_u\in \mathbb{R}^{k}$ and for each item $i$ - a vector $q_i \in \mathbb{R}^{k}$ s.t.: $$ R_{ui} \approx p_u^\top q_i $$

• $p_u$'s components sometimes can be iterpreted as user's interests in topic
• $q_i$'s components sometimes can be iterpreted as items's relevance to topic

Singular Value Decomposition

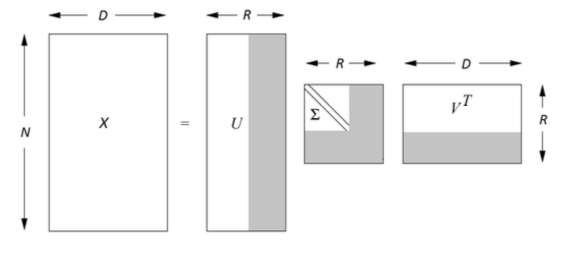
Each matrix $X\in \mathbb{R}^{n \times d}$ with rank $r$ can be decomposed as $$ X = U \Sigma V^\top ,$$ where

• $U$ - unitary matrix, which contains eigenvectors of $XX^\top$
• $V$ - unitary matrix, which contains eigenvectors of $X^\top X$
• $\Sigma$ - diagonal matrix with singular values $\sigma_i = \sqrt{\lambda_i}$

Truncated SVD

Truncated SVD with rank $K$ $$ X \approx \hat{X} = U_k \Sigma_k V_k^\top ,$$ where

• $U_k$ contains first $k$ columns of $U$
• $V_k$ contains first $k$ columns of $V$
• $\Sigma_k$ contains first $k$ diagonal elements of $\Sigma$

SVD разложение

It turns out that $$ \hat{X} = \arg \min\limits_{A\in \mathbb{R}{n \times d}, rank(A) \leq k} \| X-A \|_{Frobenius} $$

Problems

• Have to fill missing values
  • with $0$
  • with baseline predictions
• Optionally
  • $R' = R-B$ and fill with $0$
• In the end:
  • $P = U \Sigma^{1/2}$
  • $Q = \Sigma^{1/2}V^\top$
  • $\hat{R} = P^\top Q$
• How do we calculate $p_u$ for new user $u$ given his rating vector $r_u$?

Recalculation for new user

$$ p_u = \arg \min\limits_p \|r_u - Vp \|^2 = \{\text{OLS solution}\} = \left( V^\top V \right)^{-1} V^\top r_u = V^\top r_u$$

• $p_u = V^\top r_u$ is a vector of scalar products $[\langle v_1, r_u \rangle, \langle v_2, r_u \rangle, \dots, \langle v_k, r_u \rangle]$
• Backward transformation from low-dimensional representation $p_u$ to initial representation $\hat{r}_u$: $\hat{r}_u = Vp_u$

Latent Factor Model (Sparse SVD)

• Lets optimize $$ \sum\limits_{u,i}(R_{ui} - \bar{R}_u - \bar{R}_i - \langle p_u, q_i \rangle)^2 \rightarrow \min\limits_{P, Q} $$
• Using SGD and going through pairs $(u,i)$ with known $R_{ui}$: $$ p_{uk} = p_{uk} + 2\alpha \left(q_{ik}(R_{ui} - \bar{R}_u - \bar{R}_i - \langle p_u, q_i \rangle\right)$$ $$ q_{ik} = q_{ik} + 2\alpha \left(p_{uk}(R_{ui} - \bar{R}_u - \bar{R}_i - \langle p_u, q_i \rangle\right)$$

Latent Factor Model (Sparse SVD)

• Add regularization $$ \sum\limits_{u,i}(R_{ui} - \bar{R}_u - \bar{R}_i - \langle p_u, q_i \rangle)^2 + \lambda \sum_u\| p_u \|^2 + \mu\sum_i\| q_i \|^2 \rightarrow \min\limits_{P, Q} $$
• Using SGD and going through pairs $(u,i)$ with known $R_{ui}$: $$ p_{uk} = p_{uk} + 2\alpha \left(q_{ik}(R_{ui} - \bar{R}_u - \bar{R}_i - \langle p_u, q_i \rangle) - \lambda p_{uk}\right)$$ $$ q_{ik} = q_{ik} + 2\alpha \left(p_{uk}(R_{ui} - \bar{R}_u - \bar{R}_i - \langle p_u, q_i \rangle) - \mu q_{ik}\right)$$

Factorization Machines

• Represent all users and items iteractions with one-hot encoded vector (of length $d=|U|+|I|$):

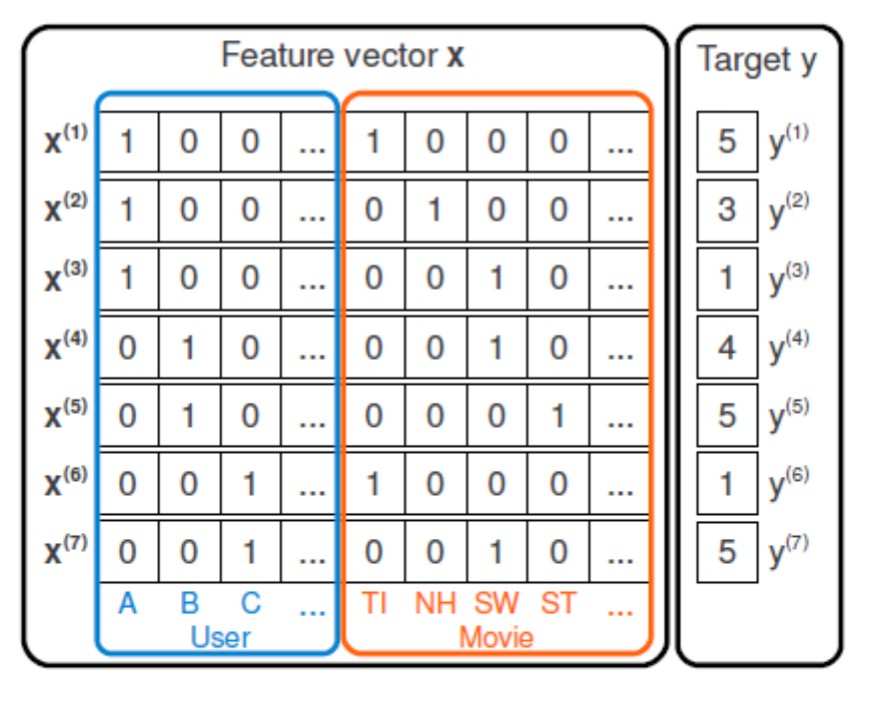
• In such feature space we can consider various models:

$$ a(x) = w_0 + \sum\limits_{i=1}^d w_i x_i \quad \text(linear)$$$$ a(x) = w_0 + \sum\limits_{i=1}^d w_i x_i + \sum\limits_{i=1,j=i+1}^d w_{ij} x_i x_j \quad \text(polynomial)$$

Factorization Machines

• Let's try to reduce the number of parameters and approximate $w_{ij}$ with $\langle v_i, v_j\rangle$, where $v_i$ is latent representation of feature $x_j$

$$ a(x) = w_0 + \sum\limits_{i=1}^d w_i x_i + \sum\limits_{i=1,j=i+1}^d \langle v_i, v_j\rangle x_i x_j \quad \text(fm)$$

Factorization Machines

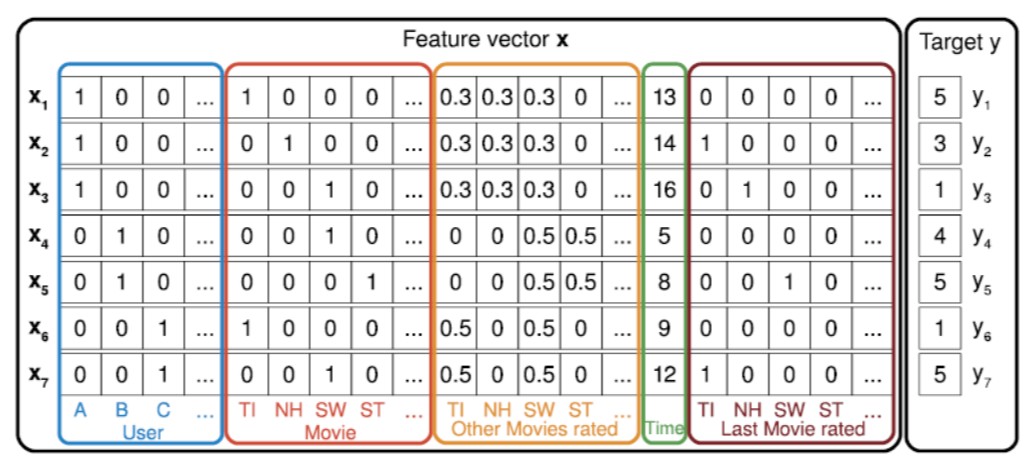
Classification-based models

• How can we adapt simple classification task to recommendation system domain?
• Any problems here?

Measuring Quality

• Ratings accuracy
  • MAE, MSE
• Event quality
  • F-score, ROC-AUC, PR-AUC
  • precision@k, recall@k
• Ranking quality
  • $DCG@k(u) = \sum\limits_{p=1}^k \frac{rel(i,p)}{\log{(p+1)}}$
  • $nDCG@k(u) = \frac{DCG@k(u)}{\max{(DCG@k(u))}}$
• What else is usefull to measure?